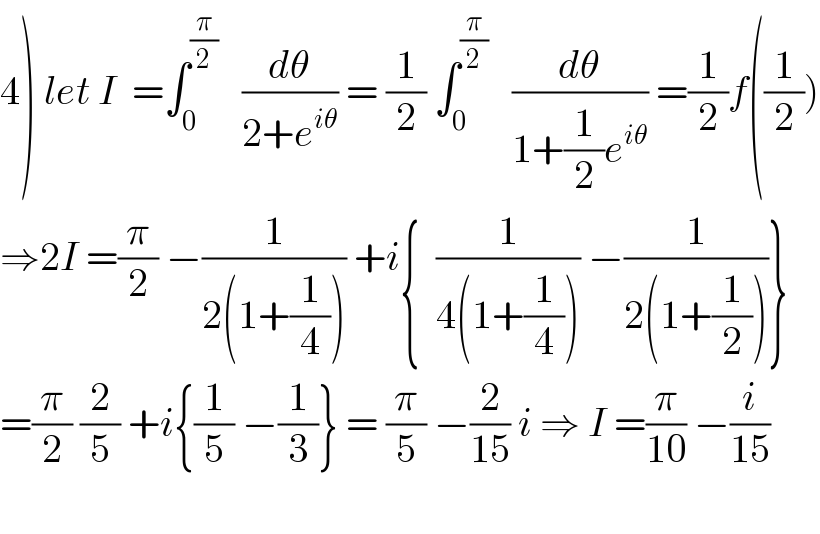Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 38706 by abdo mathsup 649 cc last updated on 28/Jun/18

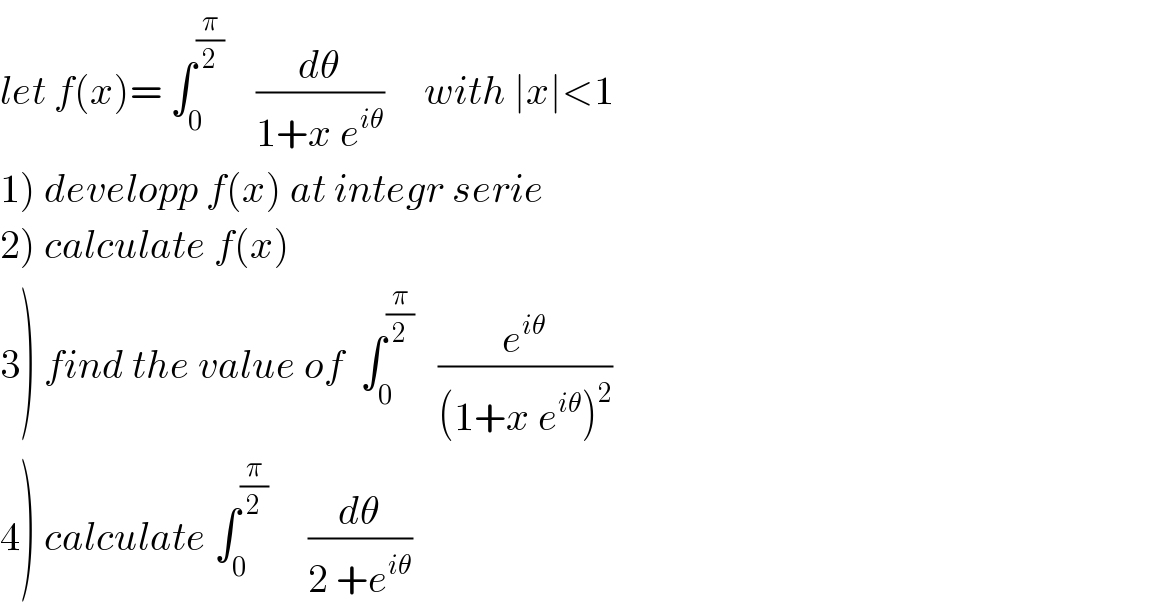
let f(x)= ∫_0 ^(π/2) (dθ/(1+x e^(iθ) )) with ∣x∣<1 1) developp f(x) at integr serie 2) calculate f(x) 3) find the value of ∫_0 ^(π/2) (e^(iθ) /((1+x e^(iθ) )^2 )) 4) calculate ∫_0 ^(π/2) (dθ/(2 +e^(iθ) ))

$${let}\:{f}\left({x}\right)=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\frac{{d}\theta}{\mathrm{1}+{x}\:{e}^{{i}\theta} }\:\:\:\:\:{with}\:\mid{x}\mid<\mathrm{1} \\ $$ $$\left.\mathrm{1}\right)\:{developp}\:{f}\left({x}\right)\:{at}\:{integr}\:{serie} \\ $$ $$\left.\mathrm{2}\right)\:{calculate}\:{f}\left({x}\right) \\ $$ $$\left.\mathrm{3}\right)\:{find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{e}^{{i}\theta} }{\left(\mathrm{1}+{x}\:{e}^{{i}\theta} \right)^{\mathrm{2}} } \\ $$ $$\left.\mathrm{4}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\:\frac{{d}\theta}{\mathrm{2}\:+{e}^{{i}\theta} } \\ $$

Commented bymaxmathsup by imad last updated on 30/Jun/18

2) we have f(x) = Σ_(n=0) ^∞ (((−1)^n )/(in)) e^((inπ)/2) x^n −Σ_(n=0) ^∞ (((−1)^n )/(in)) x^n 1) f(x) = ∫_0 ^(π/2) (Σ_(n=0) ^∞ (−1)^n x^n e^(inθ) )dθ = Σ_(n=0) ^∞ (−1)^n x^n ∫_0 ^(π/2) e^(inθ) dθ =(π/2) + Σ_(n=1) ^∞ (−1)^n x^n [(1/(in)) e^(inθ) ]_0 ^(π/2) =(π/2) −i Σ_(n=1) ^∞ (−1)^n x^n ( e^((inπ)/2) −1) f(x) =(π/2) −i Σ_(n=1) ^∞ (−1)^n ( e^((inπ)/2) −1)x^(n )

$$\left.\mathrm{2}\right)\:{we}\:{have}\:{f}\left({x}\right)\:=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{in}}\:{e}^{\frac{{in}\pi}{\mathrm{2}}} {x}^{{n}} \:\:−\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{in}}\:{x}^{{n}} \\ $$ $$\left.\mathrm{1}\right)\:{f}\left({x}\right)\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:{x}^{{n}} \:{e}^{{in}\theta} \right){d}\theta\:=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} {x}^{{n}} \:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{e}^{{in}\theta} \:{d}\theta \\ $$ $$=\frac{\pi}{\mathrm{2}}\:\:+\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:{x}^{{n}} \:\left[\frac{\mathrm{1}}{{in}}\:{e}^{{in}\theta} \right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$ $$=\frac{\pi}{\mathrm{2}}\:−{i}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} {x}^{{n}} \left(\:{e}^{\frac{{in}\pi}{\mathrm{2}}} \:−\mathrm{1}\right) \\ $$ $${f}\left({x}\right)\:=\frac{\pi}{\mathrm{2}}\:−{i}\:\sum_{{n}=\mathrm{1}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \left(\:{e}^{\frac{{in}\pi}{\mathrm{2}}} \:−\mathrm{1}\right){x}^{{n}\:} \\ $$

Commented bymaxmathsup by imad last updated on 30/Jun/18

2) we have f(x) =(π/2) −i Σ_(n=1) ^∞ (−1)^n e^((inπ)/2) x^n +i Σ_(n=1) ^∞ (−1)^n x^n but Σ_(n=1) ^∞ (−1)^n x^n −1= (1/(1+x)) −1 = ((−x)/(1+x)) Σ_(n=1) ^∞ (−1)^n e^((inπ)/2) x^n = Σ_(n=0) ^∞ (−e^((iπ)/2) x)^n −1 = (1/(1+e^((iπ)/2) x)) −1 = (1/(1+ix)) −1 = ((1−ix)/(1+x^2 )) −1 = ((−x^2 )/(1+x^2 )) −i(x/(1+x^2 )) ⇒ f(x) = (π/2) −i( ((−x^2 )/(1+x^2 )) −((ix)/(1+x^2 ))) −((ix)/(1+x)) =(π/2) −(x/(1+x^2 )) +i{ (x^2 /(1+x^2 )) −(x/(1+x))}

$$\left.\mathrm{2}\right)\:{we}\:{have}\:{f}\left({x}\right)\:=\frac{\pi}{\mathrm{2}}\:−{i}\:\sum_{{n}=\mathrm{1}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:{e}^{\frac{{in}\pi}{\mathrm{2}}} \:{x}^{{n}} \:\:+{i}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:{x}^{{n}} \:\:{but} \\ $$ $$\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:{x}^{{n}} \:−\mathrm{1}=\:\frac{\mathrm{1}}{\mathrm{1}+{x}}\:−\mathrm{1}\:=\:\frac{−{x}}{\mathrm{1}+{x}} \\ $$ $$\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:{e}^{\frac{{in}\pi}{\mathrm{2}}} \:{x}^{{n}} =\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−{e}^{\frac{{i}\pi}{\mathrm{2}}} {x}\right)^{{n}} \:−\mathrm{1}\: \\ $$ $$=\:\frac{\mathrm{1}}{\mathrm{1}+{e}^{\frac{{i}\pi}{\mathrm{2}}} {x}}\:−\mathrm{1}\:=\:\:\frac{\mathrm{1}}{\mathrm{1}+{ix}}\:−\mathrm{1}\:=\:\:\frac{\mathrm{1}−{ix}}{\mathrm{1}+{x}^{\mathrm{2}} }\:−\mathrm{1}\:=\:\frac{−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }\:−{i}\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\Rightarrow \\ $$ $${f}\left({x}\right)\:=\:\frac{\pi}{\mathrm{2}}\:−{i}\left(\:\frac{−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }\:−\frac{{ix}}{\mathrm{1}+{x}^{\mathrm{2}} }\right)\:−\frac{{ix}}{\mathrm{1}+{x}} \\ $$ $$=\frac{\pi}{\mathrm{2}}\:−\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\:+{i}\left\{\:\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }\:−\frac{{x}}{\mathrm{1}+{x}}\right\} \\ $$

Commented bymaxmathsup by imad last updated on 30/Jun/18

3) we have f(x) =∫_0 ^(π/2) (dθ/(1+x cosθ)) ⇒f^′ (x) = ∫_0 ^(π/2) ((−sinθ)/((1+cosθ)^2 )) dθ ⇒ ∫_0 ^(π/2) ((sinθ)/((1+cosθ)^2 ))dθ =−f^′ (x) .

$$\left.\mathrm{3}\right)\:{we}\:{have}\:{f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{d}\theta}{\mathrm{1}+{x}\:{cos}\theta}\:\Rightarrow{f}^{'} \left({x}\right)\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{−{sin}\theta}{\left(\mathrm{1}+{cos}\theta\right)^{\mathrm{2}} }\:{d}\theta\:\Rightarrow \\ $$ $$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{sin}\theta}{\left(\mathrm{1}+{cos}\theta\right)^{\mathrm{2}} }{d}\theta\:=−{f}^{'} \left({x}\right)\:. \\ $$

Commented bymaxmathsup by imad last updated on 30/Jun/18

4) let I =∫_0 ^(π/2) (dθ/(2+e^(iθ) )) = (1/2) ∫_0 ^(π/2) (dθ/(1+(1/2)e^(iθ) )) =(1/2)f((1/2)) ⇒2I =(π/2) −(1/(2(1+(1/4)))) +i{ (1/(4(1+(1/4)))) −(1/(2(1+(1/2))))} =(π/2) (2/5) +i{(1/5) −(1/3)} = (π/5) −(2/(15)) i ⇒ I =(π/(10)) −(i/(15))

$$\left.\mathrm{4}\right)\:{let}\:{I}\:\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{d}\theta}{\mathrm{2}+{e}^{{i}\theta} }\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{d}\theta}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}{e}^{{i}\theta} }\:=\frac{\mathrm{1}}{\mathrm{2}}{f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$ $$\Rightarrow\mathrm{2}{I}\:=\frac{\pi}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}\right)}\:+{i}\left\{\:\:\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}\right)}\:−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)}\right\} \\ $$ $$=\frac{\pi}{\mathrm{2}}\:\frac{\mathrm{2}}{\mathrm{5}}\:+{i}\left\{\frac{\mathrm{1}}{\mathrm{5}}\:−\frac{\mathrm{1}}{\mathrm{3}}\right\}\:=\:\frac{\pi}{\mathrm{5}}\:−\frac{\mathrm{2}}{\mathrm{15}}\:{i}\:\Rightarrow\:{I}\:=\frac{\pi}{\mathrm{10}}\:−\frac{{i}}{\mathrm{15}} \\ $$ $$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com