
Question and Answers Forum
Question Number 38746 by MJS last updated on 29/Jun/18
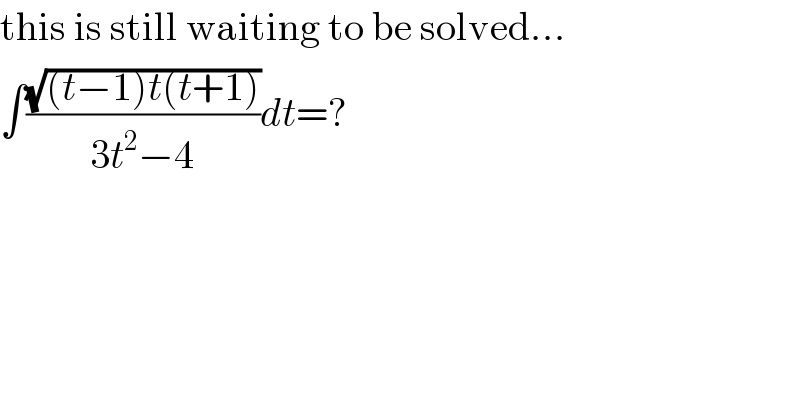
Commented by behi83417@gmail.com last updated on 29/Jun/18

Commented by prof Abdo imad last updated on 29/Jun/18

Commented by MJS last updated on 29/Jun/18

| ||
Question and Answers Forum | ||
Question Number 38746 by MJS last updated on 29/Jun/18 | ||
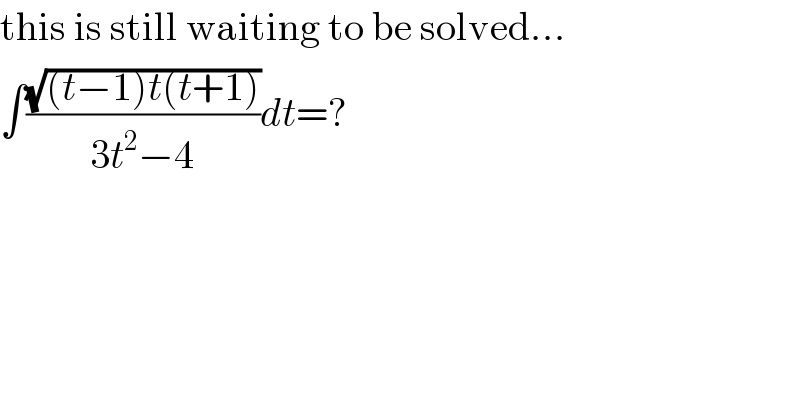 | ||
Commented by behi83417@gmail.com last updated on 29/Jun/18 | ||
 | ||
Commented by prof Abdo imad last updated on 29/Jun/18 | ||
 | ||
Commented by MJS last updated on 29/Jun/18 | ||
 | ||