Question Number 38896 by math khazana by abdo last updated on 01/Jul/18
![let A_n = ∫_0 ^n ((x[x])/(1+x^2 )) dx 1) calculate A_n 2) find lim_(n→+∞) A_n](Q38896.png)
$${let}\:{A}_{{n}} =\:\int_{\mathrm{0}} ^{{n}} \:\:\:\frac{{x}\left[{x}\right]}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{A}_{{n}} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} \\ $$
Commented by math khazana by abdo last updated on 01/Jul/18
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{A}_{{n}} =\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\int_{{k}} ^{{k}+\mathrm{1}} \:\:\:\frac{{kx}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{k}\:\int_{{k}} ^{{k}+\mathrm{1}} \:\:\frac{{xdx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\frac{{k}}{\mathrm{2}}\left({ln}\left(\mathrm{1}+\left({k}+\mathrm{1}\right)^{\mathrm{2}} \right)\:−{ln}\left(\mathrm{1}+{k}^{\mathrm{2}} \right)\right) \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\:\frac{{k}}{\mathrm{2}}{ln}\left\{\frac{\mathrm{1}\:+{k}^{\mathrm{2}} \:+\mathrm{2}{k}+\mathrm{1}}{{k}^{\mathrm{2}} \:+\mathrm{1}}\right\} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\frac{{k}}{\mathrm{2}}{ln}\left\{\:\:\frac{{k}^{\mathrm{2}} \:+\mathrm{2}{k}+\mathrm{2}}{{k}^{\mathrm{2}} \:+\mathrm{1}}\right\}\:\: \\ $$$$\left.\mathrm{2}\right)\:{ln}\left\{\:\frac{{k}^{\mathrm{2}} \:+\mathrm{2}{k}\:+\mathrm{2}}{{k}^{\mathrm{2}} \:+\mathrm{1}}\right\}={ln}\left\{\:\:\frac{{k}^{\mathrm{2}} \:+\mathrm{1}\:+\mathrm{2}{k}+\mathrm{1}}{{k}^{\mathrm{2}} \:+\mathrm{1}}\right\} \\ $$$$={ln}\left(\:\mathrm{1}+\:\frac{\mathrm{2}{k}+\mathrm{1}}{{k}^{\mathrm{2}} \:+\mathrm{1}}\right)\:{but} \\ $$$${ln}^{'} \left(\mathrm{1}+{x}\right)\:=\frac{\mathrm{1}}{\mathrm{1}+{x}}\:=\mathrm{1}−{x}\:+{o}\left({x}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{x}\right)\:={x}\:−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:+{o}\left({x}^{\mathrm{3}} \right)\:\Rightarrow \\ $$$${x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\leqslant\:{ln}\left(\mathrm{1}+{x}\right)\leqslant{x}\:\:\Rightarrow \\ $$$$\frac{\mathrm{2}{k}+\mathrm{1}}{{k}^{\mathrm{2}} \:+\mathrm{1}}\:\:−\frac{\mathrm{1}}{\mathrm{2}}\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} }{\left({k}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:\leqslant\:{ln}\left(\mathrm{1}+\frac{\mathrm{2}{k}+\mathrm{1}}{{k}^{\mathrm{2}} \:+\mathrm{1}}\right)\leqslant\:\frac{\mathrm{2}{k}+\mathrm{1}}{{k}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\frac{{k}}{\mathrm{2}}\left\{\:\frac{\mathrm{2}{k}+\mathrm{1}}{{k}^{\mathrm{2}} \:+\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} }{\left({k}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\right\}\leqslant\:\frac{{k}}{\mathrm{2}}{ln}\left(\mathrm{1}+\frac{\mathrm{2}{k}+\mathrm{1}}{{k}^{\mathrm{2}} \:+\mathrm{1}}\right) \\ $$$$\leqslant\:\frac{{k}}{\mathrm{2}}\:\frac{\mathrm{2}{k}+\mathrm{1}}{{k}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$${A}_{{n}} \:\geqslant\:\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \:\:\frac{{k}\left(\mathrm{2}{k}+\mathrm{1}\right)}{\mathrm{2}{k}^{\mathrm{2}} \:+\mathrm{2}}\:−\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \:\frac{{k}}{\mathrm{4}}\:\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} }{\left({k}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:\rightarrow+\infty \\ $$$$\left({n}\rightarrow+\infty\right)\:{so}\:{lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} =+\infty. \\ $$
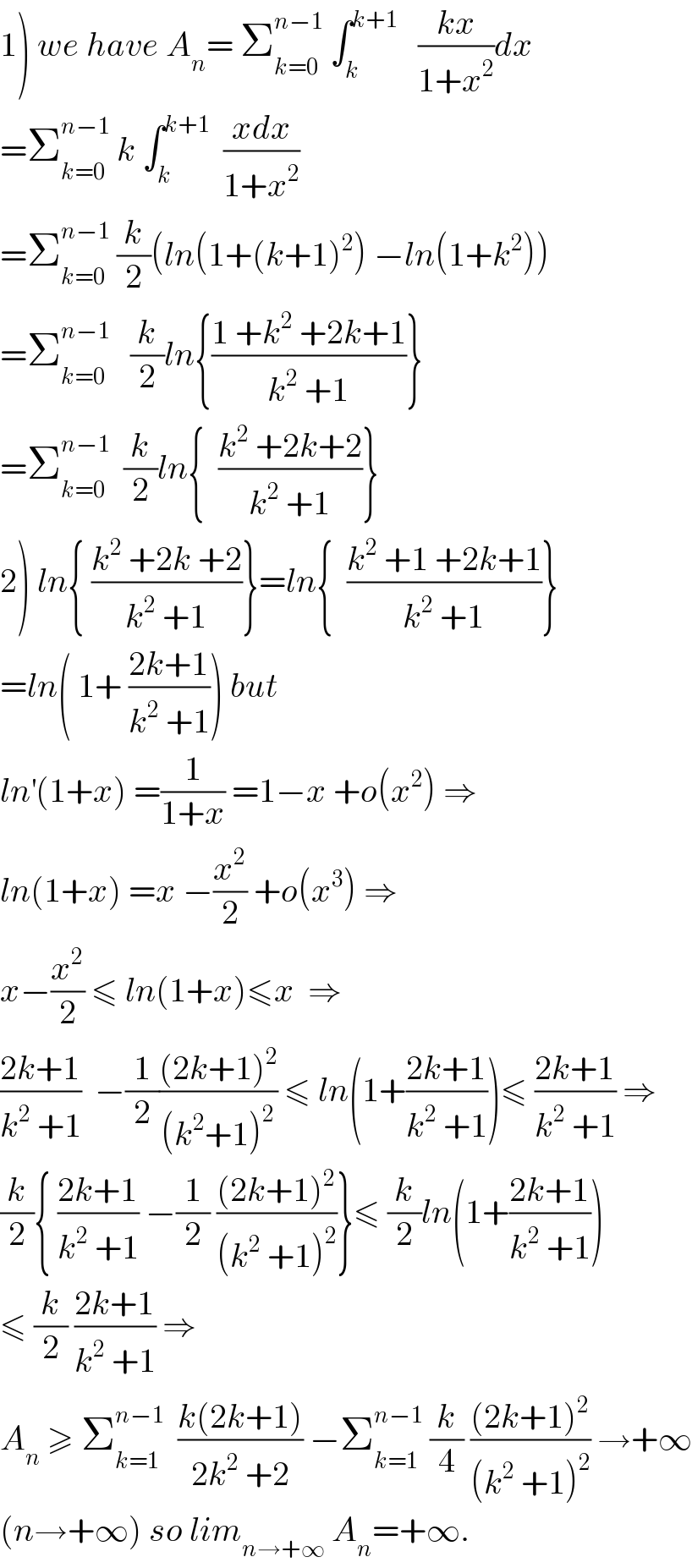
Commented by math khazana by abdo last updated on 01/Jul/18
![2) another method we have 0≤x≤n ⇒ 0≤x^2 ≤n^2 ⇒ 1≤1+x^2 ≤ 1+n^2 ⇒ (1/(1+x^2 )) ≥ (1/(1+n^2 )) ⇒ A_n ≥ (1/(1+n^2 )) ∫_0 ^n x[x]dx but ∫_0 ^n x[x]dx =Σ_(k=0) ^(n−1) ∫_k ^(k+1) kx dx =Σ_(k=0) ^(n−1) k { (((k+1)^2 )/2) −(k^2 /2)} =Σ_(k=0) ^(n−1) k { ((k^2 +2k +1−k^2 )/2)} =Σ_(k=0) ^(n−1) k ((2k+1)/2) =Σ_(k=0) ^(n−1) k^2 +(1/2) Σ_(k=0) ^(n−1) k = (((n−1)(n−1+1)(2(n−1)+1))/6) +(1/2) (((n−1)n)/2) =((n(n−1)(2n−1))/6) +(1/4)(n^2 −n) ⇒ A_n ≥ (1/(n^2 +1)){ ((n(n−1)(2n−1))/6) +(1/4)(n^2 −n)}→+∞ (n→+∞)](Q39011.png)
$$\left.\mathrm{2}\right)\:{another}\:{method}\:\:{we}\:{have}\:\mathrm{0}\leqslant{x}\leqslant{n}\:\Rightarrow \\ $$$$\mathrm{0}\leqslant{x}^{\mathrm{2}} \leqslant{n}^{\mathrm{2}} \:\Rightarrow\:\mathrm{1}\leqslant\mathrm{1}+{x}^{\mathrm{2}} \:\leqslant\:\mathrm{1}+{n}^{\mathrm{2}} \:\Rightarrow\:\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\geqslant\:\frac{\mathrm{1}}{\mathrm{1}+{n}^{\mathrm{2}} } \\ $$$$\Rightarrow\:{A}_{{n}} \geqslant\:\frac{\mathrm{1}}{\mathrm{1}+{n}^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{{n}} \:{x}\left[{x}\right]{dx}\:{but} \\ $$$$\int_{\mathrm{0}} ^{{n}} \:{x}\left[{x}\right]{dx}\:=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\int_{{k}} ^{{k}+\mathrm{1}} \:{kx}\:{dx} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} {k}\:\left\{\:\frac{\left({k}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}}\:−\frac{{k}^{\mathrm{2}} }{\mathrm{2}}\right\} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{k}\:\left\{\:\frac{{k}^{\mathrm{2}} \:+\mathrm{2}{k}\:+\mathrm{1}−{k}^{\mathrm{2}} }{\mathrm{2}}\right\} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{k}\:\frac{\mathrm{2}{k}+\mathrm{1}}{\mathrm{2}} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{k}^{\mathrm{2}} \:\:+\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{k} \\ $$$$=\:\frac{\left({n}−\mathrm{1}\right)\left({n}−\mathrm{1}+\mathrm{1}\right)\left(\mathrm{2}\left({n}−\mathrm{1}\right)+\mathrm{1}\right)}{\mathrm{6}}\:\:+\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\left({n}−\mathrm{1}\right){n}}{\mathrm{2}} \\ $$$$=\frac{{n}\left({n}−\mathrm{1}\right)\left(\mathrm{2}{n}−\mathrm{1}\right)}{\mathrm{6}}\:+\frac{\mathrm{1}}{\mathrm{4}}\left({n}^{\mathrm{2}} \:−{n}\right)\:\Rightarrow \\ $$$${A}_{{n}} \:\geqslant\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} \:+\mathrm{1}}\left\{\:\:\frac{{n}\left({n}−\mathrm{1}\right)\left(\mathrm{2}{n}−\mathrm{1}\right)}{\mathrm{6}}\:+\frac{\mathrm{1}}{\mathrm{4}}\left({n}^{\mathrm{2}} −{n}\right)\right\}\rightarrow+\infty \\ $$$$\left({n}\rightarrow+\infty\right) \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 01/Jul/18
![A_n =∫_0 ^1 ((x×0)/(1+x^2 ))dx+∫_1 ^2 ((x×1)/(1+x^2 ))dx+∫_2 ^3 ((x×2)/(1+x^2 ))+ ∫_(n−1) ^n ((x×(n−1))/(1+x^2 ))dx =(1/2)×1∫_1 ^2 ((2x)/(1+x^2 ))dx+(1/2)×2∫_2 ^3 ((2x)/(1+x^2 ))dx+(1/2)×3∫_3 ^4 ((2x)/(1+x^2 )) (1/2)×4∫_4 ^5 ((2x)/(1+x^2 ))+...+(1/2)×(n−1)∫_(n−1) ^n ((2x)/(1+x^2 ))dx =(1/2){1×∣ln(1+x^2 )∣_1 ^2 +2×∣ln(1+x^2 )∣_2 ^3 +..+ (n−1)∣ln(1+x^2 )∣_(n−1) ^n } =(1/2)[1×(ln5−ln2)+2×(ln10−ln5)+ +...+(n−1){ln(1+n^2 )−ln(1+(n−1)^2 }] =(1/2)ln{((5/2))^1 ×(((10)/5))^2 ×...×(((1+n^2 )/(1+(n−1)^2 )))^(n−1) }](Q38911.png)
$${A}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}×\mathrm{0}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}+\int_{\mathrm{1}} ^{\mathrm{2}} \frac{{x}×\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}+\int_{\mathrm{2}} ^{\mathrm{3}} \frac{{x}×\mathrm{2}}{\mathrm{1}+{x}^{\mathrm{2}} }+ \\ $$$$\:\:\int_{{n}−\mathrm{1}} ^{{n}} \frac{{x}×\left({n}−\mathrm{1}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{1}\int_{\mathrm{1}} ^{\mathrm{2}} \frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}+\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}\int_{\mathrm{2}} ^{\mathrm{3}} \frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}+\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{3}\int_{\mathrm{3}} ^{\mathrm{4}} \frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{4}\int_{\mathrm{4}} ^{\mathrm{5}} \frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }+...+\frac{\mathrm{1}}{\mathrm{2}}×\left({n}−\mathrm{1}\right)\int_{{n}−\mathrm{1}} ^{{n}} \frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{1}×\mid{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\mid_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{2}×\mid{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\mid_{\mathrm{2}} ^{\mathrm{3}} +..+\right. \\ $$$$\left.\left({n}−\mathrm{1}\right)\mid{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\mid_{{n}−\mathrm{1}} ^{{n}} \right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{1}×\left({ln}\mathrm{5}−{ln}\mathrm{2}\right)+\mathrm{2}×\left({ln}\mathrm{10}−{ln}\mathrm{5}\right)+\right. \\ $$$$\:\:+...+\left({n}−\mathrm{1}\right)\left\{{ln}\left(\mathrm{1}+{n}^{\mathrm{2}} \right)−{ln}\left(\mathrm{1}+\left({n}−\mathrm{1}\right)^{\mathrm{2}} \right\}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left\{\left(\frac{\mathrm{5}}{\mathrm{2}}\right)^{\mathrm{1}} ×\left(\frac{\mathrm{10}}{\mathrm{5}}\right)^{\mathrm{2}} ×...×\left(\frac{\mathrm{1}+{n}^{\mathrm{2}} }{\mathrm{1}+\left({n}−\mathrm{1}\right)^{\mathrm{2}} }\right)^{{n}−\mathrm{1}} \right\} \\ $$$$ \\ $$