
Question and Answers Forum
Question Number 39020 by maxmathsup by imad last updated on 01/Jul/18
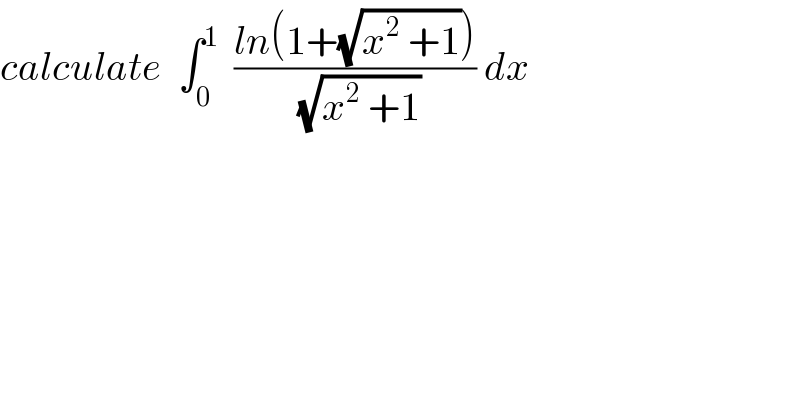
Answered by behi83417@gmail.com last updated on 02/Jul/18
![x=tgt⇒dx=(1+tg^2 t)dt I=∫((ln(1+sect))/(sect)).sec^2 tdt= =∫sect.ln(1+sect)dt= sect.ln(1+sect)−∫sect.((sint.sec^2 t)/(1+sect))dt= =do−∫((sint.(1/(cos^3 t)))/(1+(1/(cost))))dt=do−∫((sintdt)/(cos^3 t+cos^2 t)) cost=u⇒∫((−sintdt)/(cos^3 t+cos^2 t))=∫(du/(u^3 +u^2 ))= =∫(du/(u^2 (u+1)))=∫[((−1)/u)+(1/u^2 )+(1/(u+1))]du =−lnu−u+ln(u+1)+c= =−lncost−cost+ln(1+cost)+c= =ln((1+cost)/(cost))−cost+c=ln(1+sect)−cost+c ⇒I=(√(1+x^2 )).ln(1+(√(1+x^2 )))+ln(1+(√(1+x^2 )))−(1/(√(1+x^2 )))+c= =(1+(√(1+x^2 )))ln(1+(√(1+x^2 )))−(1/(√(1+x^2 )))+c.■](Q39052.png)
| ||
Question and Answers Forum | ||
Question Number 39020 by maxmathsup by imad last updated on 01/Jul/18 | ||
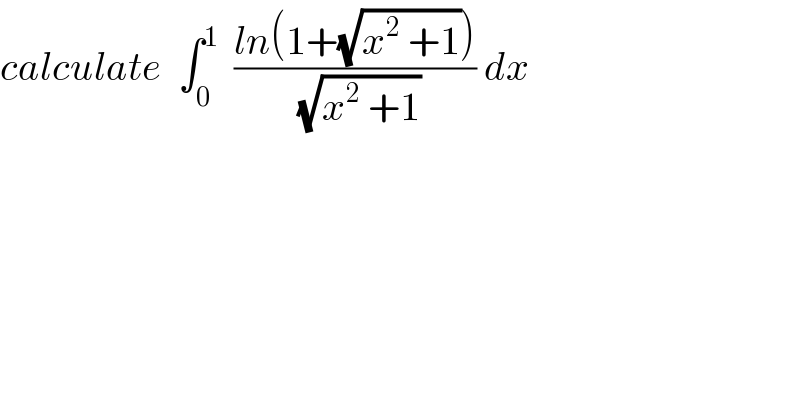 | ||
Answered by behi83417@gmail.com last updated on 02/Jul/18 | ||
![x=tgt⇒dx=(1+tg^2 t)dt I=∫((ln(1+sect))/(sect)).sec^2 tdt= =∫sect.ln(1+sect)dt= sect.ln(1+sect)−∫sect.((sint.sec^2 t)/(1+sect))dt= =do−∫((sint.(1/(cos^3 t)))/(1+(1/(cost))))dt=do−∫((sintdt)/(cos^3 t+cos^2 t)) cost=u⇒∫((−sintdt)/(cos^3 t+cos^2 t))=∫(du/(u^3 +u^2 ))= =∫(du/(u^2 (u+1)))=∫[((−1)/u)+(1/u^2 )+(1/(u+1))]du =−lnu−u+ln(u+1)+c= =−lncost−cost+ln(1+cost)+c= =ln((1+cost)/(cost))−cost+c=ln(1+sect)−cost+c ⇒I=(√(1+x^2 )).ln(1+(√(1+x^2 )))+ln(1+(√(1+x^2 )))−(1/(√(1+x^2 )))+c= =(1+(√(1+x^2 )))ln(1+(√(1+x^2 )))−(1/(√(1+x^2 )))+c.■](Q39052.png) | ||
| ||