
Question and Answers Forum
Question Number 39023 by maxmathsup by imad last updated on 01/Jul/18
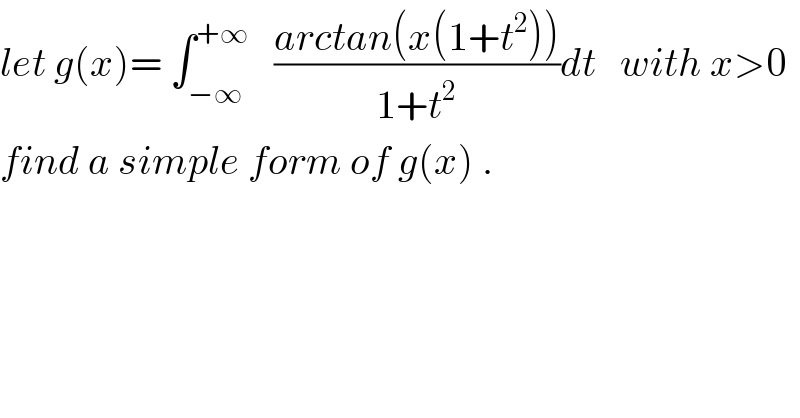
Commented bymath khazana by abdo last updated on 08/Jul/18

| ||
Question and Answers Forum | ||
Question Number 39023 by maxmathsup by imad last updated on 01/Jul/18 | ||
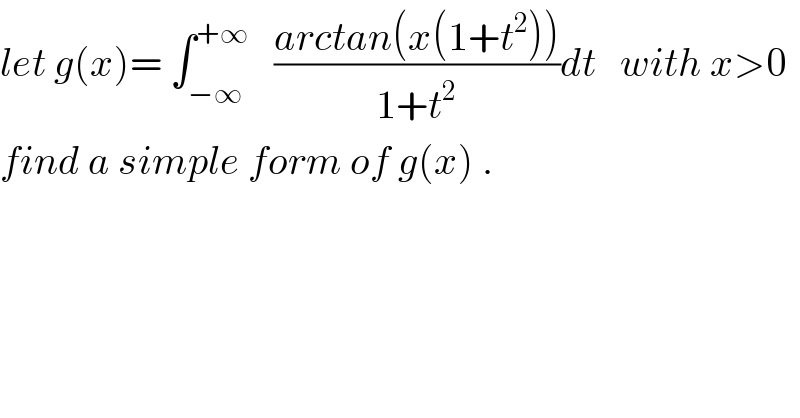 | ||
Commented bymath khazana by abdo last updated on 08/Jul/18 | ||
 | ||