
Question and Answers Forum
Question Number 39035 by maxmathsup by imad last updated on 01/Jul/18
![find f(t) =∫_0 ^∞ sin(x)e^(−t [x]) dx with t>0](Q39035.png)
Commented bymaxmathsup by imad last updated on 02/Jul/18
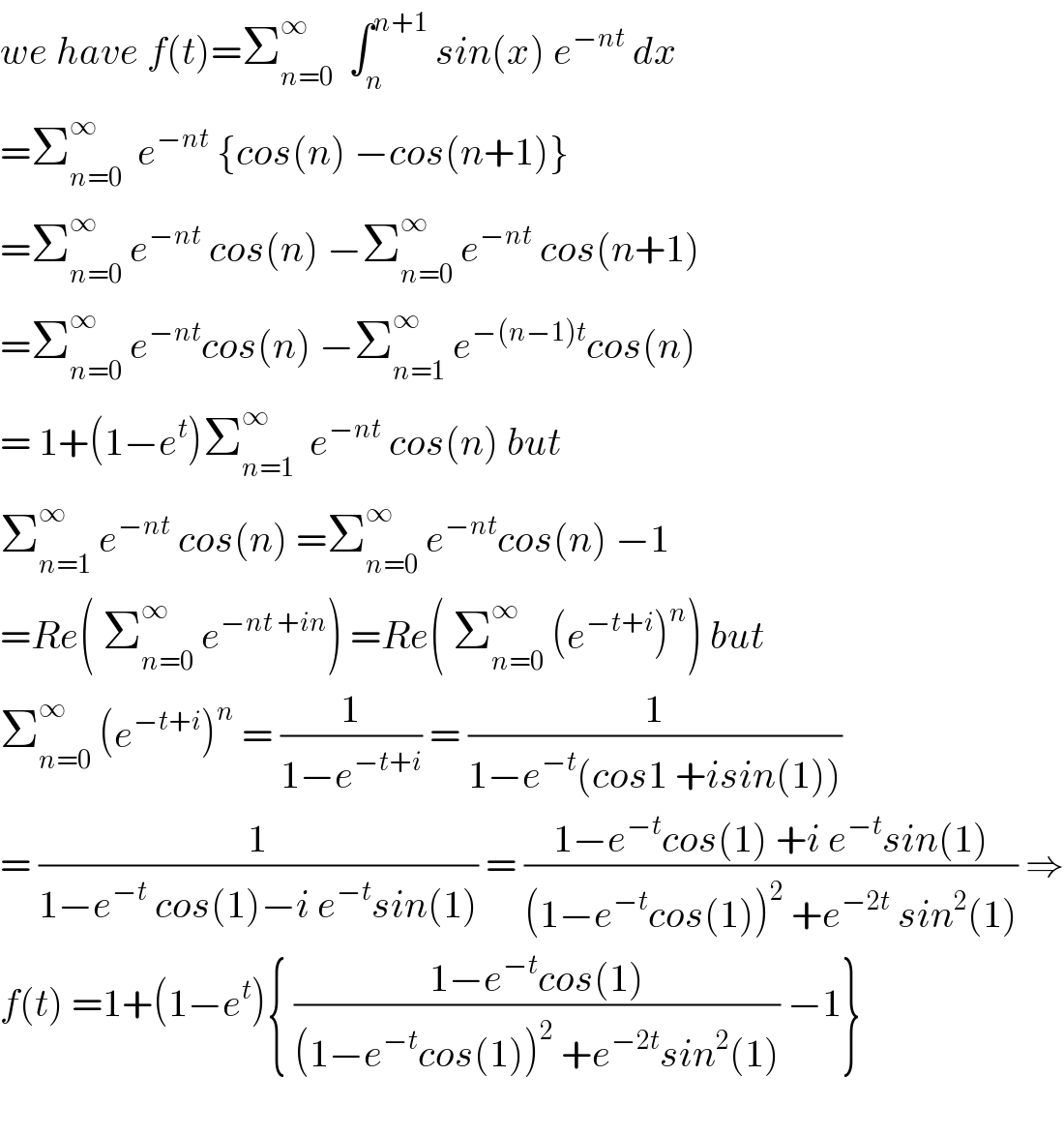
| ||
Question and Answers Forum | ||
Question Number 39035 by maxmathsup by imad last updated on 01/Jul/18 | ||
![find f(t) =∫_0 ^∞ sin(x)e^(−t [x]) dx with t>0](Q39035.png) | ||
Commented bymaxmathsup by imad last updated on 02/Jul/18 | ||
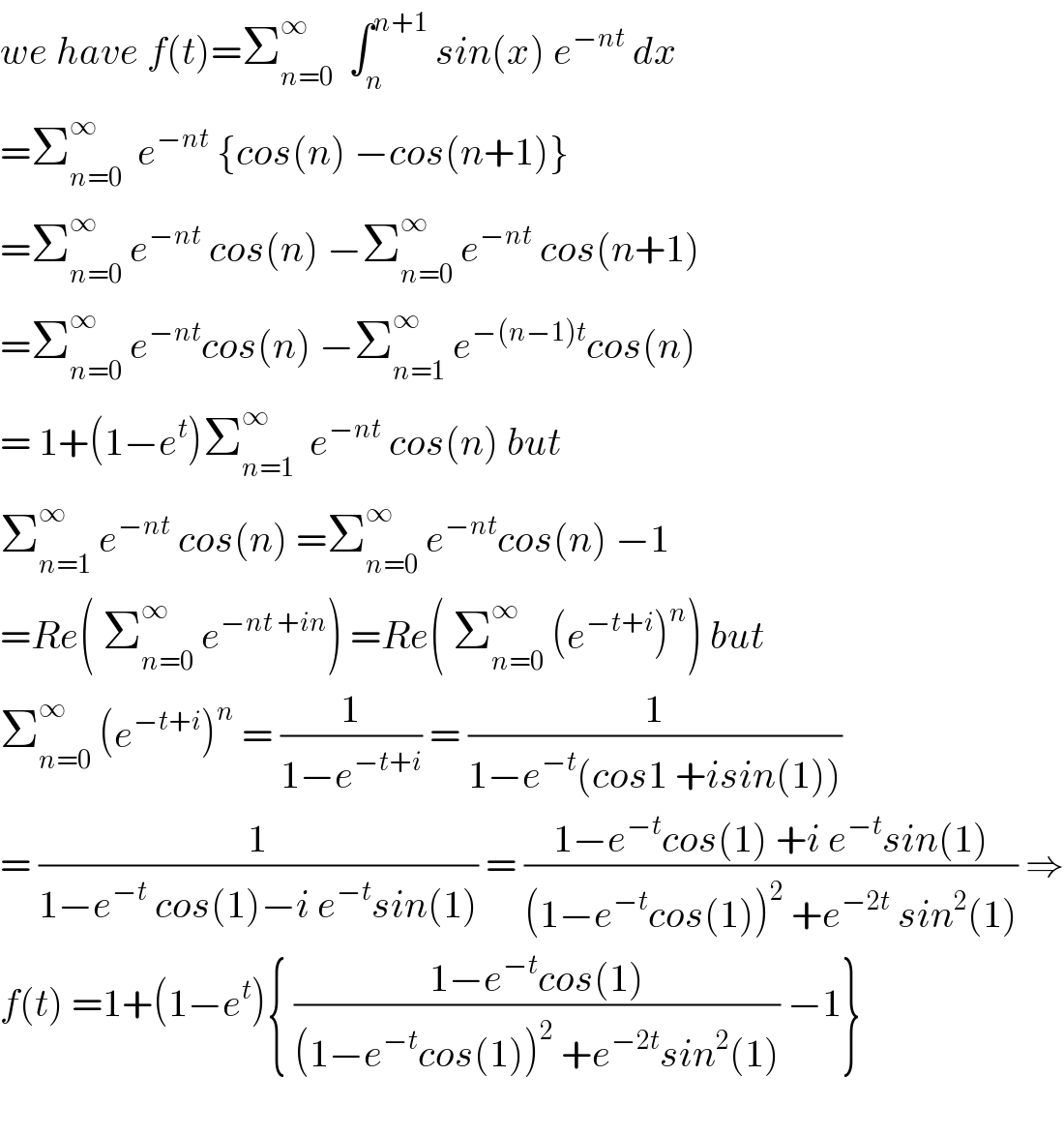 | ||