let f(z) = (z/(z^2 −z+2)) developp f at integr serie.


Question and Answers Forum

All Questions Topic List
Relation and Functions Questions
Previous in All Question Next in All Question
Previous in Relation and Functions Next in Relation and Functions
Question Number 39038 by maxmathsup by imad last updated on 01/Jul/18

$l e t f (z) = \frac{z}{z^{2} - z + 2}$ $d e v e l o p p f a t i n t e g r s e r i e .$
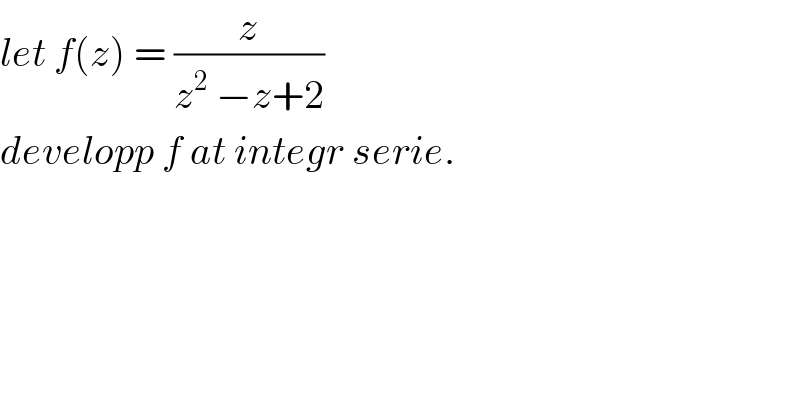
Commented by prof Abdo imad last updated on 02/Jul/18
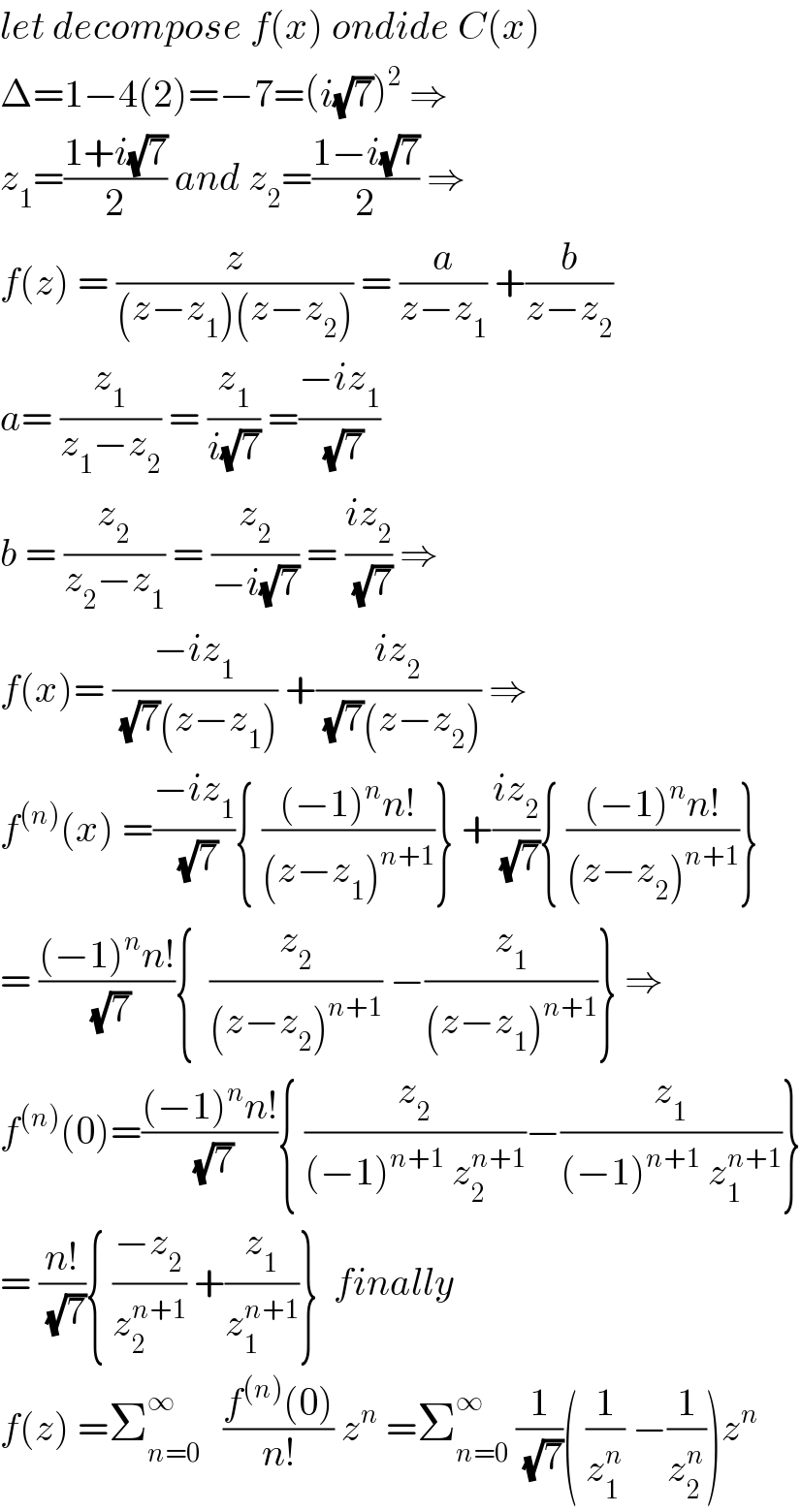
$let decompose f(x) ondide C(x) Δ=1−4(2)=−7=(i(√7))^2 ⇒ z_1 =((1+i(√7))/2) and z_2 =((1−i(√7))/2) ⇒ f(z) = (z/((z−z_1 )(z−z_2 ))) = (a/(z−z_1 )) +(b/(z−z_2 )) a= (z_1 /(z_1 −z_2 )) = (z_1 /(i(√7))) =((−iz_1 )/(√7)) b = (z_2 /(z_2 −z_1 )) = (z_2 /(−i(√7))) = ((iz_2 )/(√7)) ⇒ f(x)= ((−iz_1 )/((√7)(z−z_1 ))) +((iz_2 )/((√7)(z−z_2 ))) ⇒ f^((n)) (x) =((−iz_1 )/(√7)){ (((−1)^n n!)/((z−z_1 )^(n+1) ))} +((iz_2 )/(√7)){ (((−1)^n n!)/((z−z_2 )^(n+1) ))} = (((−1)^n n!)/(√7)){ (z_2 /((z−z_2 )^(n+1) )) −(z_1 /((z−z_1 )^(n+1) ))} ⇒ f^((n)) (0)=(((−1)^n n!)/(√7)){ (z_2 /((−1)^(n+1) z_2 ^(n+1) ))−(z_1 /((−1)^(n+1) z_1 ^(n+1) ))} = ((n!)/(√7)){ ((−z_2 )/z_2 ^(n+1) ) +(z_1 /z_1 ^(n+1) )} finally f(z) =Σ_(n=0) ^∞ ((f^((n)) (0))/(n!)) z^n =Σ_(n=0) ^∞ (1/(√7))( (1/z_1 ^n ) −(1/z_2 ^n ))z^n$
$l e t d e c o m p o s e f (x) o n d i d e C (x)$ $Δ = 1 - 4 (2) = - 7 = {(i \sqrt{7})}^{2} \Rightarrow$ $z_{1} = \frac{1 + i \sqrt{7}}{2} a n d z_{2} = \frac{1 - i \sqrt{7}}{2} \Rightarrow$ $f (z) = \frac{z}{(z - z_{1}) (z - z_{2})} = \frac{a}{z - z_{1}} + \frac{b}{z - z_{2}}$ $a = \frac{z_{1}}{z_{1} - z_{2}} = \frac{z_{1}}{i \sqrt{7}} = \frac{- {i z}_{1}}{\sqrt{7}}$ $b = \frac{z_{2}}{z_{2} - z_{1}} = \frac{z_{2}}{- i \sqrt{7}} = \frac{{i z}_{2}}{\sqrt{7}} \Rightarrow$ $f (x) = \frac{- {i z}_{1}}{\sqrt{7} (z - z_{1})} + \frac{{i z}_{2}}{\sqrt{7} (z - z_{2})} \Rightarrow$ $f^{(n)} (x) = \frac{- {i z}_{1}}{\sqrt{7}} {\frac{{(- 1)}^{n} n!}{{(z - z_{1})}^{n + 1}}} + \frac{{i z}_{2}}{\sqrt{7}} {\frac{{(- 1)}^{n} n!}{{(z - z_{2})}^{n + 1}}}$ $= \frac{{(- 1)}^{n} n!}{\sqrt{7}} {\frac{z_{2}}{{(z - z_{2})}^{n + 1}} - \frac{z_{1}}{{(z - z_{1})}^{n + 1}}} \Rightarrow$ $f^{(n)} (0) = \frac{{(- 1)}^{n} n!}{\sqrt{7}} {\frac{z_{2}}{{(- 1)}^{n + 1} z_{2}^{n + 1}} - \frac{z_{1}}{{(- 1)}^{n + 1} z_{1}^{n + 1}}}$ $= \frac{n!}{\sqrt{7}} {\frac{- z_{2}}{z_{2}^{n + 1}} + \frac{z_{1}}{z_{1}^{n + 1}}} f i n a l l y$ $f (z) = \sum_{n = 0}^{\infty} \frac{f^{(n)} (0)}{n!} z^{n} = \sum_{n = 0}^{\infty} \frac{1}{\sqrt{7}} (\frac{1}{z_{1}^{n}} - \frac{1}{z_{2}^{n}}) z^{n}$
Commented by prof Abdo imad last updated on 02/Jul/18
$let simplify (1/z_1 ^n ) −(1/z_2 ^n ) = ((z_2 ^n −z_1 ^n )/((z_1 z_2 )^n )) = (((((1−i(√7))/2))^n −( ((1+i(√7))/2))^n )/2) = −(1/2^(n+1) ) { (1+i(√7))^n −(1−i(√7))^n } =−(1/2^(n+1) ) { Σ_(k=0) ^n C_n ^k (i(√7))^k −Σ_(k=0) ^n C_n ^k (−i(√7))^k } =((−1)/2^(n+1) ) Σ_(k=0) ^n C_n ^k { (i(√7))^k −(−i(√7))^k } =((−1)/2^(n+1) ) Σ_(p=0) ^([((n−1)/2)]) C_n ^(2p+1) { 2i(−1)^p 7^p (√7) } =((−i)/2^n ) (√7)Σ_(p=0) ^([((n−1)/2)]) C_n ^(2p+1) (−7)^p ⇒ f(z)=Σ_(n=0) ^∞ ((−i)/2^n ){ Σ_(p=0) ^([((n−1)/2)]) (−7)^(p ) C_n ^(2p+1) }z^n$
$l e t s i m p l i f y \frac{1}{z_{1}^{n}} - \frac{1}{z_{2}^{n}}$ $= \frac{z_{2}^{n} - z_{1}^{n}}{{(z_{1} z_{2})}^{n}} = \frac{{(\frac{1 - i \sqrt{7}}{2})}^{n} - {(\frac{1 + i \sqrt{7}}{2})}^{n}}{2}$ $= - \frac{1}{2^{n + 1}} {{(1 + i \sqrt{7})}^{n} - {(1 - i \sqrt{7})}^{n}}$ $= - \frac{1}{2^{n + 1}} {\sum_{k = 0}^{n} C_{n}^{k} {(i \sqrt{7})}^{k} - \sum_{k = 0}^{n} C_{n}^{k} {(- i \sqrt{7})}^{k}}$ $= \frac{- 1}{2^{n + 1}} \sum_{k = 0}^{n} C_{n}^{k} {{(i \sqrt{7})}^{k} - {(- i \sqrt{7})}^{k}}$ $= \frac{- 1}{2^{n + 1}} \sum_{p = 0}^{[\frac{n - 1}{2}]} C_{n}^{2 p + 1} {2 i {(- 1)}^{p} 7^{p} \sqrt{7}}$ $= \frac{- i}{2^{n}} \sqrt{7} \sum_{p = 0}^{[\frac{n - 1}{2}]} C_{n}^{2 p + 1} {(- 7)}^{p} \Rightarrow$ $f (z) = \sum_{n = 0}^{\infty} \frac{- i}{2^{n}} {\sum_{p = 0}^{[\frac{n - 1}{2}]} {(- 7)}^{p} C_{n}^{2 p + 1}} z^{n}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum