Question Number 39120 by math khazana by abdo last updated on 02/Jul/18
![let A_n = ∫_1 ^n (([(√(1+x^2 ))] −[x])/x^2 ) dx (n integr ≥1) 1) calculate A_n 2) find lim_(n→+∞) A_n](Q39120.png)
$${let}\:{A}_{{n}} =\:\int_{\mathrm{1}} ^{{n}} \:\frac{\left[\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right]\:−\left[{x}\right]}{{x}^{\mathrm{2}} }\:{dx}\:\:\left({n}\:{integr}\:\geqslant\mathrm{1}\right) \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{A}_{{n}} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} \: \\ $$
Commented by math khazana by abdo last updated on 04/Jul/18
![we have A_n = Σ_(k=1) ^n ∫_k ^(k+1) (([(√(1+x^2 ))]−k)/x^2 )dx but k≤x<k+1 ⇒ k^2 ≤x^2 <(k+1)^2 ⇒ k^2 +1 ≤1+x^2 ≤1+ (k+1)^2 ⇒(√(1+k^2 )) ≤(√(1+x^2 )) <(√(1+(k+1)^2 )) ⇒ (√(1+k^2 )) ≤(√(1+x^2 <)) (√(k^2 +2k+2))≤k+2 ⇒ k ≤ (√(1+x^2 <)) k+2 ⇒[(√(1+x^2 ))]=k or k+1 A_n =Σ_(k=1) ^n ∫_k ^(k+1) ((k+1−k)/x^2 )dx=Σ_(k=1) ^n ∫_k ^(k+1) (dx/x^2 ) =Σ_(k=1) ^n [−(1/x)]_k ^(k+1) = Σ_(k=1) ^n ( (1/k) −(1/(k+1))) =1−(1/2) +(1/2) −(1/3) +....(1/n) −(1/(n+1)) =1−(1/(n+1)) ⇒ A_n = (n/(n+1)) 2) its clear that lim_(n→+∞) A_n =1 .](Q39268.png)
$${we}\:{have}\:{A}_{{n}} =\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\int_{{k}} ^{{k}+\mathrm{1}} \:\:\:\frac{\left[\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right]−{k}}{{x}^{\mathrm{2}} }{dx}\:\:{but} \\ $$$${k}\leqslant{x}<{k}+\mathrm{1}\:\Rightarrow\:{k}^{\mathrm{2}} \leqslant{x}^{\mathrm{2}} <\left({k}+\mathrm{1}\right)^{\mathrm{2}} \:\Rightarrow \\ $$$${k}^{\mathrm{2}} \:+\mathrm{1}\:\leqslant\mathrm{1}+{x}^{\mathrm{2}} \leqslant\mathrm{1}+\:\left({k}+\mathrm{1}\right)^{\mathrm{2}} \:\Rightarrow\sqrt{\mathrm{1}+{k}^{\mathrm{2}} }\:\leqslant\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:<\sqrt{\mathrm{1}+\left({k}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\:\sqrt{\mathrm{1}+{k}^{\mathrm{2}} }\:\leqslant\sqrt{\mathrm{1}+{x}^{\mathrm{2}} <}\:\sqrt{{k}^{\mathrm{2}} \:+\mathrm{2}{k}+\mathrm{2}}\leqslant{k}+\mathrm{2}\:\Rightarrow \\ $$$${k}\:\leqslant\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} <}\:{k}+\mathrm{2}\:\:\Rightarrow\left[\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right]={k}\:{or}\:{k}+\mathrm{1}\: \\ $$$${A}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\int_{{k}} ^{{k}+\mathrm{1}} \:\frac{{k}+\mathrm{1}−{k}}{{x}^{\mathrm{2}} }{dx}=\sum_{{k}=\mathrm{1}} ^{{n}} \:\int_{{k}} ^{{k}+\mathrm{1}} \:\frac{{dx}}{{x}^{\mathrm{2}} } \\ $$$$=\sum_{{k}=\mathrm{1}} ^{{n}} \:\left[−\frac{\mathrm{1}}{{x}}\right]_{{k}} ^{{k}+\mathrm{1}} \:=\:\sum_{{k}=\mathrm{1}} ^{{n}} \left(\:\frac{\mathrm{1}}{{k}}\:−\frac{\mathrm{1}}{{k}+\mathrm{1}}\right) \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{3}}\:+....\frac{\mathrm{1}}{{n}}\:−\frac{\mathrm{1}}{{n}+\mathrm{1}}\:=\mathrm{1}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\:\Rightarrow \\ $$$${A}_{{n}} =\:\frac{{n}}{{n}+\mathrm{1}} \\ $$$$\left.\mathrm{2}\right)\:{its}\:{clear}\:{that}\:\:{lim}_{{n}\rightarrow+\infty} \:\:{A}_{{n}} =\mathrm{1}\:. \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 03/Jul/18
![x (√(1+x^2 )) [(√(1+x^2 )) ] [x_ ] [(√(1+x^2 )) ]−[x] 1 (√2) =1.41 1 1 0 1.5 (√(3.25)) =1.8 1 1 0 2 (√5) =2.23 2 2 0 2.5 (√(7.25))=2.69 2 2 0 3 (√(10)) =3.16 3 3 0 4 (√(17)) = 4.12 4 4 0 k (√(1+k^2 )) =k+△k k k 0 when 1 >△k>0 wait](Q39179.png)
$${x}\:\:\:\:\:\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\:\:\:\:\:\left[\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\right]\:\:\:\:\left[{x}_{} \right]\:\:\:\:\left[\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\right]−\left[{x}\right] \\ $$$$\mathrm{1}\:\:\:\:\:\:\sqrt{\mathrm{2}}\:=\mathrm{1}.\mathrm{41}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0} \\ $$$$\mathrm{1}.\mathrm{5}\:\:\sqrt{\mathrm{3}.\mathrm{25}}\:=\mathrm{1}.\mathrm{8}\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0} \\ $$$$\mathrm{2}\:\:\:\:\:\:\:\:\sqrt{\mathrm{5}}\:\:\:=\mathrm{2}.\mathrm{23}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0} \\ $$$$\mathrm{2}.\mathrm{5}\:\:\:\sqrt{\mathrm{7}.\mathrm{25}}=\mathrm{2}.\mathrm{69}\:\:\:\mathrm{2}\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0} \\ $$$$\mathrm{3}\:\:\:\:\:\:\sqrt{\mathrm{10}}\:=\mathrm{3}.\mathrm{16}\:\:\:\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0} \\ $$$$\mathrm{4}\:\:\:\:\:\:\:\:\sqrt{\mathrm{17}}\:=\:\mathrm{4}.\mathrm{12}\:\:\:\:\:\:\:\mathrm{4}\:\:\:\:\:\:\mathrm{4}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\: \\ $$$$ \\ $$$${k}\:\:\:\:\:\:\sqrt{\mathrm{1}+{k}^{\mathrm{2}} }\:\:={k}+\bigtriangleup{k}\:\:\:{k}\:\:\:\:\:{k}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0} \\ $$$${when}\:\:\mathrm{1}\:>\bigtriangleup{k}>\mathrm{0}\: \\ $$$${wait} \\ $$$$ \\ $$
Commented by abdo.msup.com last updated on 03/Jul/18
$${but}\:{you}\:{know}\:{that}\:{the}\:{train}\:{dont}\:{wait}... \\ $$
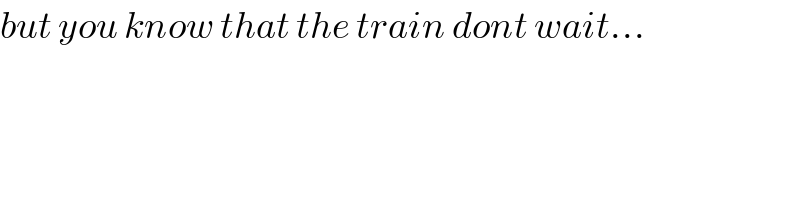
Commented by tanmay.chaudhury50@gmail.com last updated on 03/Jul/18
Commented by tanmay.chaudhury50@gmail.com last updated on 03/Jul/18
![f(x)=[(√(1+x^2 )) ]−[x] from graph it is clear that f(x)=[(√(1+x^2 )) ]−[x] is zero when n>x≥1 so the value of intregal is zero...pls check](Q39196.png)
$${f}\left({x}\right)=\left[\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\right]−\left[{x}\right] \\ $$$${from}\:{graph}\:{it}\:{is}\:{clear}\:{that}\:{f}\left({x}\right)=\left[\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\right]−\left[{x}\right] \\ $$$${is}\:{zero}\:{when}\:{n}>{x}\geqslant\mathrm{1} \\ $$$${so}\:{the}\:{value}\:{of}\:{intregal}\:\:{is}\:{zero}...{pls}\:{check} \\ $$
Commented by math khazana by abdo last updated on 03/Jul/18
$${miracylous}\:{graph}\:{for}\:{this}\:{function}\:{it}\:{s}\:{like} \\ $$$${a}\:{rail}\:{ways}... \\ $$