
Question and Answers Forum
Question Number 39222 by behi83417@gmail.com last updated on 04/Jul/18

Commented by math khazana by abdo last updated on 04/Jul/18
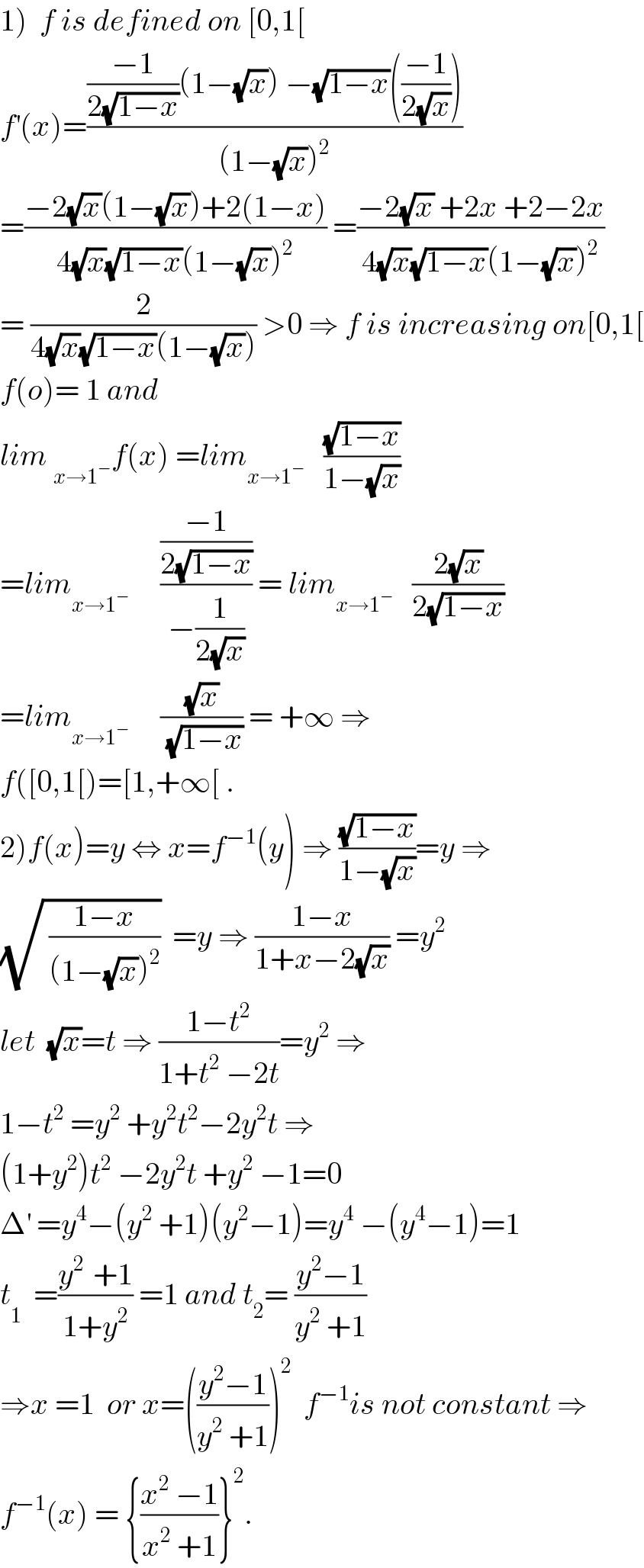
Commented by maxmathsup by imad last updated on 04/Jul/18
![3)let I = ∫_0 ^((√2)/2) ((√(1−x))/(1−(√x)))dx changement (√x)=t give I = ∫_0 ^(1/((^4 (√2)))) ((√(1−t^2 ))/(1−t)) 2t dt I =−2 ∫_0 ^2^(−(1/4)) ((1−t−1)/(1−t))(√(1−t^2 )) dt =−2 ∫_0 ^2^(−(1/4)) (√(1−t^2 )) + 2 ∫_0 ^2^(−(1/4)) ((√(1−t^2 ))/(1−t)) dt ∫_0 ^2^(−(1/4)) (√(1−t^2 ))dt =_(t=sinα) ∫_0 ^(arcsin(2^(−(1/4)) )) cosα cosα dα = (1/2) ∫_0 ^(arcsin(2^(−(1/4)) )) (1+cos(2α))dα=(1/2)arcsin(2^(−(1/4)) ) +(1/4) sin(2arcsin(2^(−(1/4)) )) ∫_0 ^(2^(−(1/4)) ) ((√(1−t^2 ))/(1−t)) =_(t=sinα) ∫_0 ^(arcsin(2^(−(1/4)) )) ((cosα)/(1−sinα)) cosα dα = ∫_0 ^(arcsin(2^(−(1/4)) )) ((1−sin^2 α)/(1−sinα)) dα =∫_0 ^(arcsin(2^(−(1/4)) )) (1+sinα)dα =arcsin(2^(−(1/4)) ) +[−cosα]_0 ^(arsin(2^(−(1/4)) )) =arcsin(2^(−(1/4)) ) +1−cos(arcsin(2^(−(1/4)) )) so the value of I is known.](Q39234.png)
Commented by behi83417@gmail.com last updated on 04/Jul/18
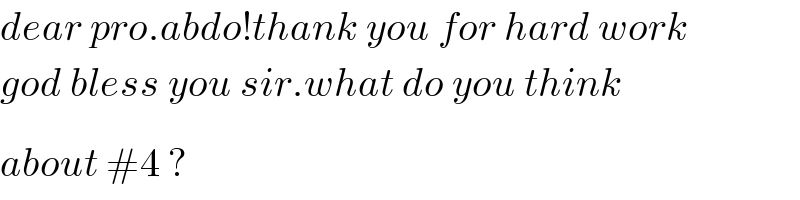
Commented by math khazana by abdo last updated on 04/Jul/18
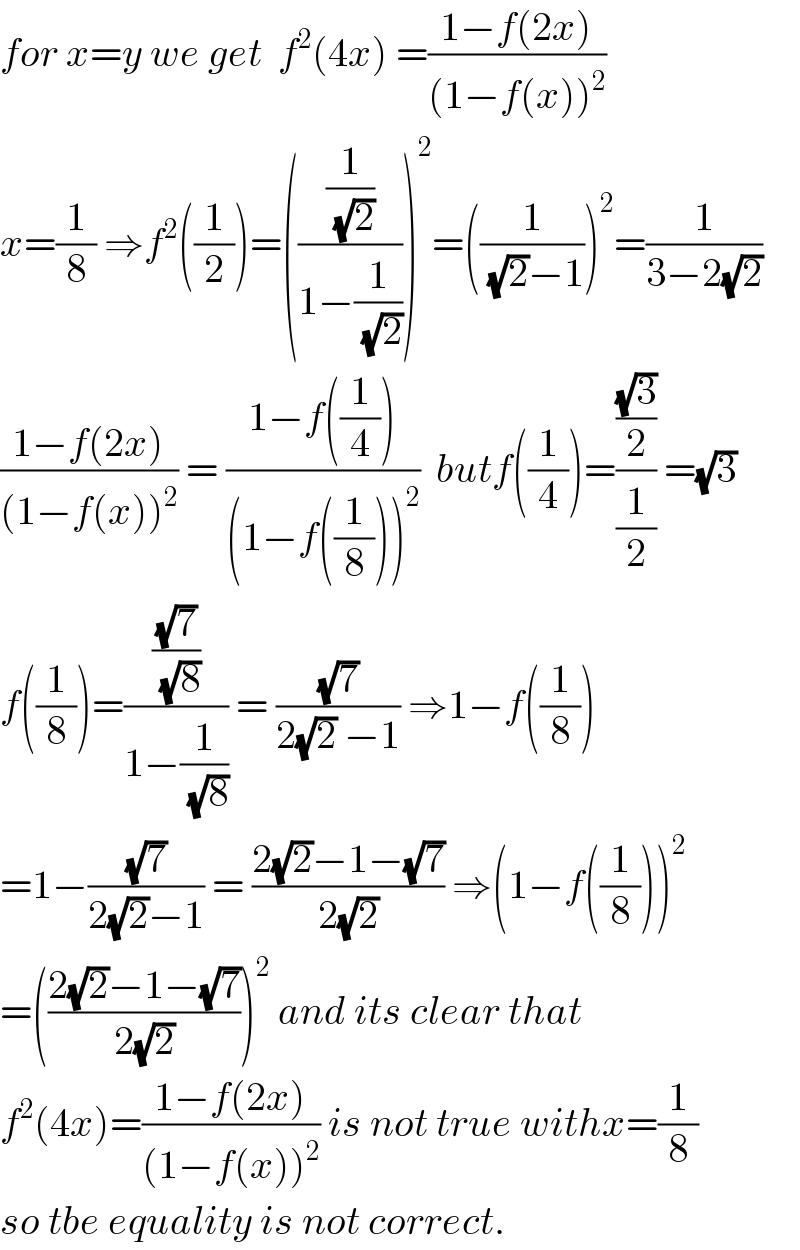
Commented by math khazana by abdo last updated on 04/Jul/18
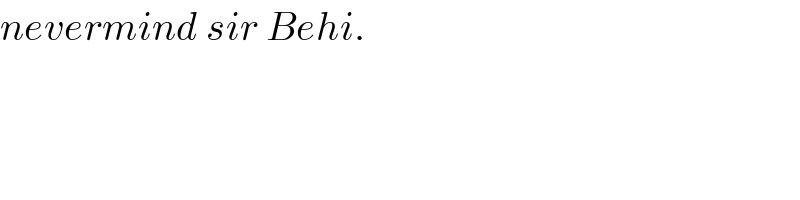
Answered by MJS last updated on 04/Jul/18
![y=((√(1−x))/(1−(√x))) ⇒ x∈[0; 1[ ∧ y∈[1; +∞[ f^(−1) (x)=(((x^2 −1)/(x^2 +1)))^2 with x∈[1; +∞[ ∧ y∈[0; 1[ ∫((√(1−x))/(1−(√x)))dx=∫(((1+(√x))(√(1−x)))/((1+(√x))(1−(√x))))dx= =∫(((√(1−x))+(√(x−x^2 )))/(1−x))dx=∫(dx/(√(1−x)))+∫(√(x/(1−x)))dx= [t=(√x) → dx=2(√x)dt] 2∫(t/(√(1−t^2 )))dt+2∫(t^2 /(√(1−t^2 )))dt= 2∫(t/(√(1−t^2 )))dt=−2(√(1−t^2 ))=−2(√(1−x)) 2∫(t^2 /(√(1−t^2 )))dt= [u=arcsin t → dt=(√(1−t^2 ))du] =2∫sin^2 u du=u−sin u cos u = =arcsin t −t(√(1−t^2 ))=arcsin (√(x ))−(√x)(√(1−x)) =arcsin (√(x ))−(2+(√x))(√(1−x))+C ∫_0 ^((√2)/2) ((√(1−x))/(1−(√x)))dx≈1.46146 but ∫_0 ^1 ((√(1−x))/(1−(√x)))dx=2+(π/2) (4) is not true for the given function](Q39228.png)
Commented by behi83417@gmail.com last updated on 04/Jul/18

