
Question Number 3928 by Filup last updated on 24/Dec/15

$$\mathrm{Is}\:\mathrm{this}\:\mathrm{solvable}: \\ $$$$ \\ $$$${y}=\lfloor{f}\left({x}\right)\rfloor\:\:\:\:\:\:\:\:\:\mathrm{floor}\:\mathrm{function} \\ $$$$\frac{{dy}}{{dx}}=??? \\ $$
Commented by Yozzii last updated on 25/Dec/15
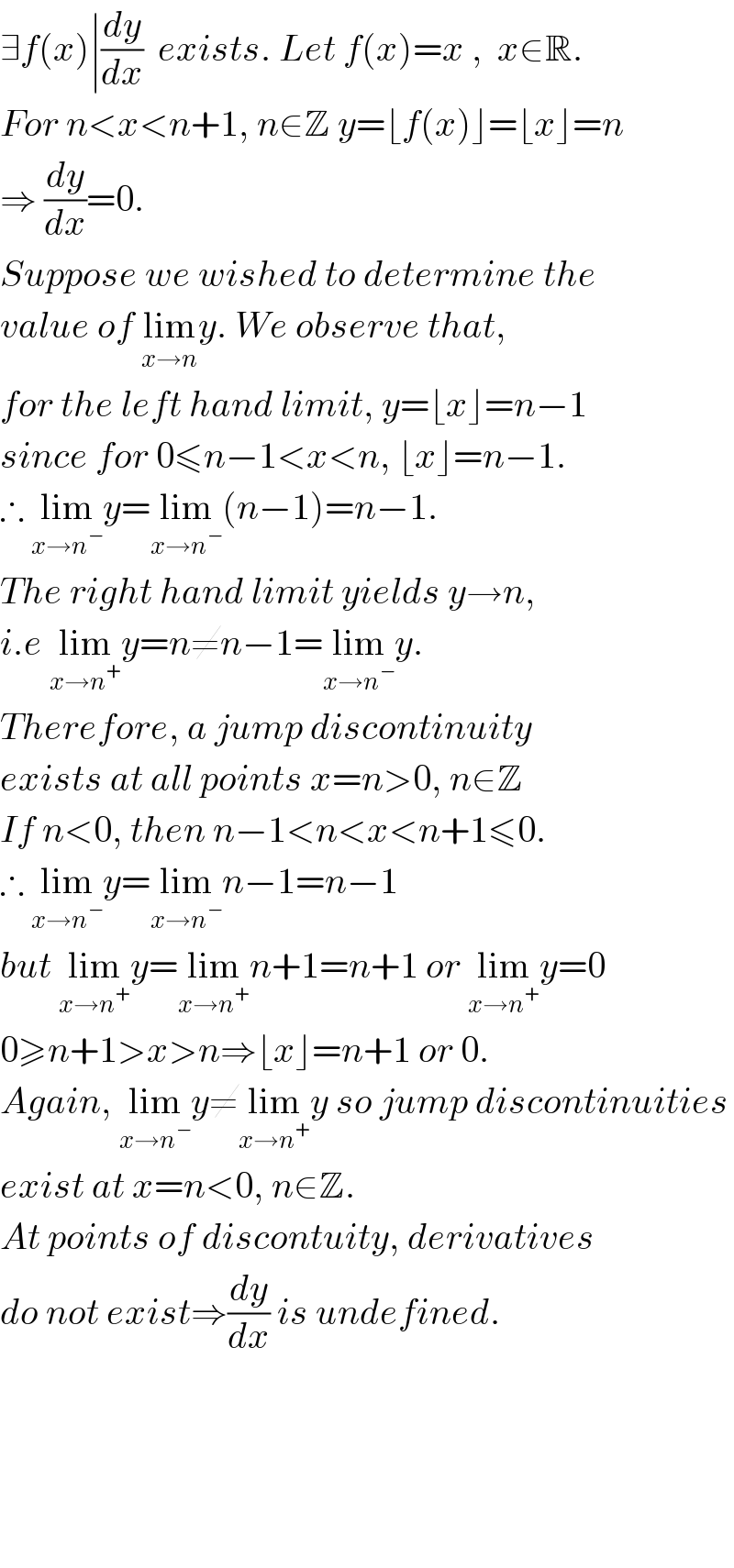
$$\exists{f}\left({x}\right)\mid\frac{{dy}}{{dx}}\:\:{exists}.\:{Let}\:{f}\left({x}\right)={x}\:,\:\:{x}\in\mathbb{R}. \\ $$$${For}\:{n}<{x}<{n}+\mathrm{1},\:{n}\in\mathbb{Z}\:{y}=\lfloor{f}\left({x}\right)\rfloor=\lfloor{x}\rfloor={n} \\ $$$$\Rightarrow\:\frac{{dy}}{{dx}}=\mathrm{0}.\: \\ $$$${Suppose}\:{we}\:{wished}\:{to}\:{determine}\:{the} \\ $$$${value}\:{of}\:\underset{{x}\rightarrow{n}} {\mathrm{lim}}{y}.\:{We}\:{observe}\:{that}, \\ $$$${for}\:{the}\:{left}\:{hand}\:{limit},\:{y}=\lfloor{x}\rfloor={n}−\mathrm{1} \\ $$$${since}\:{for}\:\mathrm{0}\leqslant{n}−\mathrm{1}<{x}<{n},\:\lfloor{x}\rfloor={n}−\mathrm{1}. \\ $$$$\therefore\:\underset{{x}\rightarrow{n}^{−} } {\mathrm{lim}}{y}=\underset{{x}\rightarrow{n}^{−} } {\mathrm{lim}}\left({n}−\mathrm{1}\right)={n}−\mathrm{1}. \\ $$$${The}\:{right}\:{hand}\:{limit}\:{yields}\:{y}\rightarrow{n}, \\ $$$${i}.{e}\:\underset{{x}\rightarrow{n}^{+} } {\mathrm{lim}}{y}={n}\neq{n}−\mathrm{1}=\underset{{x}\rightarrow{n}^{−} } {\mathrm{lim}}{y}. \\ $$$${Therefore},\:{a}\:{jump}\:{discontinuity}\: \\ $$$${exists}\:{at}\:{all}\:{points}\:{x}={n}>\mathrm{0},\:{n}\in\mathbb{Z} \\ $$$${If}\:{n}<\mathrm{0},\:{then}\:{n}−\mathrm{1}<{n}<{x}<{n}+\mathrm{1}\leqslant\mathrm{0}. \\ $$$$\therefore\:\underset{{x}\rightarrow{n}^{−} } {\mathrm{lim}}{y}=\underset{{x}\rightarrow{n}^{−} } {\mathrm{lim}}{n}−\mathrm{1}={n}−\mathrm{1} \\ $$$${but}\:\underset{{x}\rightarrow{n}^{+} } {\mathrm{lim}}{y}=\underset{{x}\rightarrow{n}^{+} } {\mathrm{lim}}{n}+\mathrm{1}={n}+\mathrm{1}\:{or}\:\underset{{x}\rightarrow{n}^{+} } {\mathrm{lim}}{y}=\mathrm{0} \\ $$$$\mathrm{0}\geqslant{n}+\mathrm{1}>{x}>{n}\Rightarrow\lfloor{x}\rfloor={n}+\mathrm{1}\:{or}\:\mathrm{0}. \\ $$$${Again},\:\underset{{x}\rightarrow{n}^{−} } {\mathrm{lim}}{y}\neq\underset{{x}\rightarrow{n}^{+} } {\mathrm{lim}}{y}\:{so}\:{jump}\:{discontinuities} \\ $$$${exist}\:{at}\:{x}={n}<\mathrm{0},\:{n}\in\mathbb{Z}. \\ $$$${At}\:{points}\:{of}\:{discontuity},\:{derivatives} \\ $$$${do}\:{not}\:{exist}\Rightarrow\frac{{dy}}{{dx}}\:{is}\:{undefined}. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by 123456 last updated on 26/Dec/15

