
Question Number 3929 by Filup last updated on 25/Dec/15
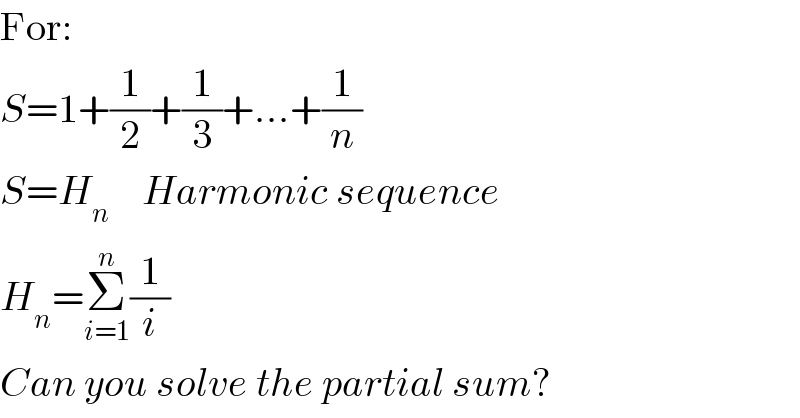
$$\mathrm{For}: \\ $$$${S}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+...+\frac{\mathrm{1}}{{n}} \\ $$$${S}={H}_{{n}} \:\:\:\:{Harmonic}\:{sequence} \\ $$$${H}_{{n}} =\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{i}} \\ $$$${Can}\:{you}\:{solve}\:{the}\:{partial}\:{sum}? \\ $$
Commented by Yozzii last updated on 25/Dec/15

$${Wolfram}\:{Alpha}\:{gives}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{H}_{{n}} =\psi_{\mathrm{0}} \left({n}+\mathrm{1}\right)+\gamma \\ $$$${where}\:\gamma−{Euler}\:{Mascheroni}\:{constant} \\ $$$$\psi_{\mathrm{0}} \left({z}\right)\:{is}\:{the}\:{digamma}\:{function}\:{defined} \\ $$$${by}\:{the}\:{logarithmic}\:{derivative}\:{of}\:{the} \\ $$$${gamma}\:{function}\:\Gamma\left({z}\right). \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\psi_{\mathrm{0}} \left({z}\right)=\frac{{d}}{{dz}}\left\{{ln}\Gamma\left({z}\right)\right\}=\frac{\Gamma^{'} \left({z}\right)}{\Gamma\left({z}\right)} \\ $$$${The}\:{digamma}\:{function}\:{satisfies}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\psi_{\mathrm{0}} \left({z}\right)=\int_{\mathrm{0}} ^{\infty} \left(\frac{{e}^{−{t}} }{{t}}−\frac{{e}^{−{zt}} }{\mathrm{1}−{e}^{−{t}} }\right){dt}. \\ $$$${For}\:{z}\equiv{n}\:,\:{n}\in\mathbb{Z}^{+} , \\ $$$$\psi_{\mathrm{0}} \left({n}\right)=−\gamma+\underset{{i}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\frac{\mathrm{1}}{{i}}\Rightarrow{H}_{{n}−\mathrm{1}} =\psi_{\mathrm{0}} \left({n}\right)+\gamma. \\ $$$$ \\ $$
