
Question Number 39338 by rahul 19 last updated on 05/Jul/18
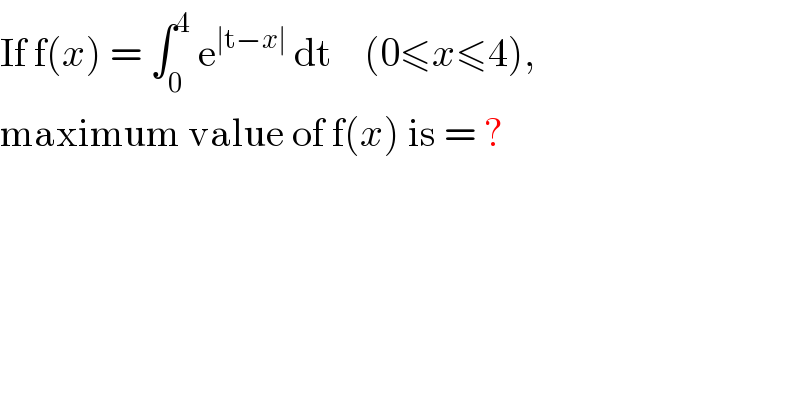
$$\mathrm{If}\:\mathrm{f}\left({x}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{4}} \:\mathrm{e}^{\mid\mathrm{t}−{x}\mid} \:\mathrm{dt}\:\:\:\:\left(\mathrm{0}\leqslant{x}\leqslant\mathrm{4}\right), \\ $$$$\mathrm{maximum}\:\mathrm{value}\:\mathrm{of}\:\mathrm{f}\left({x}\right)\:\mathrm{is}\:=\:? \\ $$
Commented by math khazana by abdo last updated on 06/Jul/18
![we have f(x)= ∫_0 ^x e^(x−t∣) dt +∫_x ^4 e^(t−x) dt =e^x [ −e^(−t) ]_0 ^x +e^(−x) [ e^t ]_x ^4 =e^x (1−e^(−x) ) +e^(−x) ( e^4 −e^x ) =e^x −1 +e^4 e^(−x) −1 =e^x +e^4 e^(−x) −2 f^′ (x)= e^x −e^4 e^(−x) =e^x (1−e^4 e^(−2x) )so f^′ (x)=0 ⇔ 1−e^4 e^(−2x) =0⇔e^(−2x) = e^(−4) ⇔x=2 f^′ (x)≥0 ⇔ 1−e^4 e^(−2x) ≥0 ⇔e^4 e^(−2x) ≤1 ⇔ e^(−2x) ≤ e^(−4) ⇔ −2x≤−4 ⇔ x≥2 so f is increazing on [2,4] decreasing on [0,2]⇒ max f(x)=f(0) or f(4) but f(0)=e^4 −1 and f(4) =e^4 −1 =f(0) ⇒ max f(x)=f(0)=e^4 −1](Q39481.png)
$${we}\:{have}\:{f}\left({x}\right)=\:\int_{\mathrm{0}} ^{{x}} \:{e}^{{x}−{t}\mid} {dt}\:+\int_{{x}} ^{\mathrm{4}} \:{e}^{{t}−{x}} \:{dt} \\ $$$$={e}^{{x}} \:\:\left[\:−{e}^{−{t}} \right]_{\mathrm{0}} ^{{x}} \:\:+{e}^{−{x}} \:\left[\:{e}^{{t}} \right]_{{x}} ^{\mathrm{4}} \\ $$$$={e}^{{x}} \left(\mathrm{1}−{e}^{−{x}} \right)\:+{e}^{−{x}} \left(\:{e}^{\mathrm{4}} \:−{e}^{{x}} \right) \\ $$$$={e}^{{x}} \:−\mathrm{1}\:+{e}^{\mathrm{4}} \:{e}^{−{x}} \:−\mathrm{1}\:={e}^{{x}} \:+{e}^{\mathrm{4}} \:{e}^{−{x}} \:−\mathrm{2} \\ $$$${f}^{'} \left({x}\right)=\:{e}^{{x}} \:−{e}^{\mathrm{4}} \:{e}^{−{x}} \:={e}^{{x}} \left(\mathrm{1}−{e}^{\mathrm{4}} \:{e}^{−\mathrm{2}{x}} \right){so} \\ $$$${f}^{'} \left({x}\right)=\mathrm{0}\:\Leftrightarrow\:\mathrm{1}−{e}^{\mathrm{4}} \:{e}^{−\mathrm{2}{x}} =\mathrm{0}\Leftrightarrow{e}^{−\mathrm{2}{x}} \:=\:{e}^{−\mathrm{4}} \:\Leftrightarrow{x}=\mathrm{2} \\ $$$${f}^{'} \left({x}\right)\geqslant\mathrm{0}\:\Leftrightarrow\:\mathrm{1}−{e}^{\mathrm{4}} \:{e}^{−\mathrm{2}{x}} \geqslant\mathrm{0}\:\Leftrightarrow{e}^{\mathrm{4}} \:{e}^{−\mathrm{2}{x}} \:\leqslant\mathrm{1}\:\Leftrightarrow \\ $$$${e}^{−\mathrm{2}{x}} \leqslant\:{e}^{−\mathrm{4}} \:\:\Leftrightarrow\:−\mathrm{2}{x}\leqslant−\mathrm{4}\:\Leftrightarrow\:{x}\geqslant\mathrm{2}\:\:{so}\:{f}\:{is} \\ $$$${increazing}\:{on}\:\left[\mathrm{2},\mathrm{4}\right]\:{decreasing}\:{on}\:\left[\mathrm{0},\mathrm{2}\right]\Rightarrow \\ $$$${max}\:{f}\left({x}\right)={f}\left(\mathrm{0}\right)\:{or}\:{f}\left(\mathrm{4}\right)\:{but} \\ $$$${f}\left(\mathrm{0}\right)={e}^{\mathrm{4}} \:−\mathrm{1}\:\:{and}\:{f}\left(\mathrm{4}\right)\:={e}^{\mathrm{4}} \:−\mathrm{1}\:={f}\left(\mathrm{0}\right)\:\Rightarrow \\ $$$${max}\:{f}\left({x}\right)={f}\left(\mathrm{0}\right)={e}^{\mathrm{4}} \:−\mathrm{1} \\ $$
Commented by rahul 19 last updated on 05/Jul/18
prof ans is (e⁴ - 1 )
Answered by ajfour last updated on 05/Jul/18
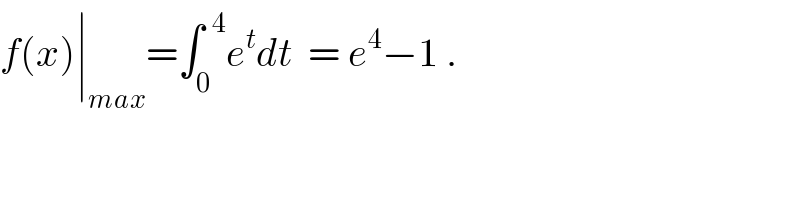
$${f}\left({x}\right)\mid_{{max}} =\int_{\mathrm{0}} ^{\:\:\mathrm{4}} {e}^{{t}} {dt}\:\:=\:{e}^{\mathrm{4}} −\mathrm{1}\:. \\ $$
Commented by rahul 19 last updated on 05/Jul/18
Thank you sir .
Answered by MJS last updated on 06/Jul/18
![(d/dx)[∫e^(∣t−x∣) dt]=−e^(∣t−x∣) ⇒ ⇒ (d/dx)[∫_0 ^4 e^(∣t−x∣) dt]=−e^(∣4−x∣) +e^(∣x∣) =f′(x) f′′(x)=sign(4−x)e^(∣4−x∣) +sign(x)e^(∣x∣) f′(x)=0 ⇒ ∣x∣=∣4−x∣ ⇒ x=2 f′′(2)=2e^2 >0 ⇒ f(x) has an absolute minimum at x=2 ⇒ maximum is at the borders of given interval ⇒ max(f(x))=f(0)=f(4)=e^4 −1](Q39428.png)
$$\frac{{d}}{{dx}}\left[\int\mathrm{e}^{\mid{t}−{x}\mid} {dt}\right]=−\mathrm{e}^{\mid{t}−{x}\mid} \:\Rightarrow \\ $$$$\Rightarrow\:\frac{{d}}{{dx}}\left[\underset{\mathrm{0}} {\overset{\mathrm{4}} {\int}}\mathrm{e}^{\mid{t}−{x}\mid} {dt}\right]=−\mathrm{e}^{\mid\mathrm{4}−{x}\mid} +\mathrm{e}^{\mid{x}\mid} ={f}'\left({x}\right) \\ $$$${f}''\left({x}\right)=\mathrm{sign}\left(\mathrm{4}−{x}\right)\mathrm{e}^{\mid\mathrm{4}−{x}\mid} +\mathrm{sign}\left({x}\right)\mathrm{e}^{\mid{x}\mid} \\ $$$${f}'\left({x}\right)=\mathrm{0}\:\Rightarrow\:\mid{x}\mid=\mid\mathrm{4}−{x}\mid\:\Rightarrow\:{x}=\mathrm{2} \\ $$$${f}''\left(\mathrm{2}\right)=\mathrm{2e}^{\mathrm{2}} >\mathrm{0}\:\Rightarrow\:{f}\left({x}\right)\:\mathrm{has}\:\mathrm{an}\:\mathrm{absolute}\:\mathrm{minimum} \\ $$$$\:\:\:\:\:\mathrm{at}\:{x}=\mathrm{2}\:\Rightarrow\:\mathrm{maximum}\:\mathrm{is}\:\mathrm{at}\:\mathrm{the}\:\mathrm{borders}\:\mathrm{of} \\ $$$$\:\:\:\:\:\mathrm{given}\:\mathrm{interval}\:\Rightarrow\:\mathrm{max}\left({f}\left({x}\right)\right)={f}\left(\mathrm{0}\right)={f}\left(\mathrm{4}\right)=\mathrm{e}^{\mathrm{4}} −\mathrm{1}\: \\ $$$$ \\ $$
