Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 39374 by maxmathsup by imad last updated on 05/Jul/18

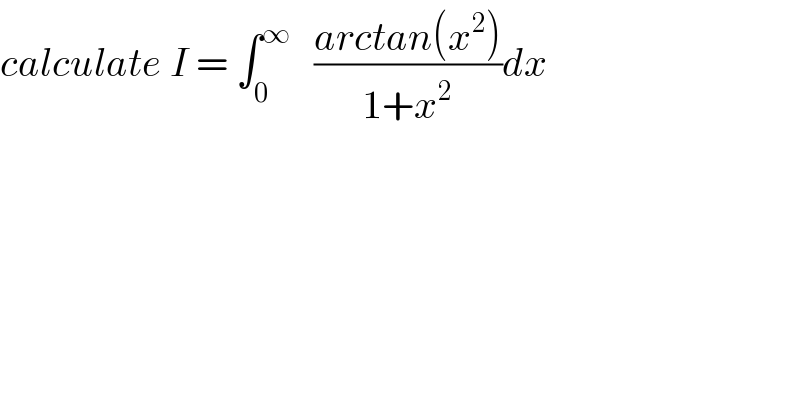
calculate I = ∫_0 ^∞ ((arctan(x^2 ))/(1+x^2 ))dx

$${calculate}\:{I}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{arctan}\left({x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$

Commented by math khazana by abdo last updated on 07/Jul/18

let f(t) = ∫_0 ^∞ ((arctan(tx^2 ))/(1+x^2 ))dx with t≥0 f^′ (t) = ∫_0 ^∞ (x^2 /((1+x^2 )(1+t^2 x^4 )))dx ⇒ 2f^′ (x)= ∫_(−∞) ^(+∞) (x^2 /((1+x^2 )(1+t^2 x^4 )))dx let ϕ(z) = (z^2 /((1+z^2 )(1+t^2 z^4 ))) ϕ(z) = (z^2 /((1+z^2 )t^2 (z^4 +(1/t^2 )))) = (z^2 /(t^2 (z−i)(z+i)(z^2 −(i/t))(z^2 +(i/t)))) = (z^2 /(t^2 (z−i)(z+i)(z −(e^(i(π/4)) /(√t)))(z +(e^((iπ)/4) /(√t)))(z−(e^(−((iπ)/4)) /(√t)))(z+(e^(−((iπ)/4)) /(√t))))) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ Res(ϕ,i) +Res(ϕ,(e^((iπ)/4) /(√t))) +Res(ϕ,−(e^(−((iπ)/4)) /(√t)))} Res(ϕ,i) = ((−1)/(t^2 (2i)(1+(1/t^2 )))) =((−1)/(2i(t^2 +1))) Res(ϕ, (e^((iπ)/4) /(√t))) = ((i/t)/(t^2 (1+(i/t))(2 (e^((iπ)/4) /(√t)))(2(i/t)))) = (i/(4t^3 ( ((t+i)/t)) ((e^((iπ)/4) /(√t))) (i/t))) =((i e^(−((iπ)/4)) (√t))/(4t(t+i)i)) =(((√t) e^(−((iπ)/4)) )/(4t(t+i))) Res(ϕ,−(e^(−((iπ)/4)) /(√t))) = ((−(i/t))/(t^2 (−(i/t) +1)(−2 (e^(−((iπ)/4)) /(√t)))(((−2i)/t)))) = ((−1)/(4t^3 ( ((−i+t)/t)) (e^(−((iπ)/4)) /(√t)) (1/t))) = −(((√t) e^((iπ)/4) )/(4t(t−i))) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ ((−1)/(2i(t^2 +1))) +((√t)/(4t))( − (e^((iπ)/4) /(t−i)) + (e^(−((iπ)/4)) /(t+i)))} = ((−π)/(t^2 +1)) −((iπ(√t))/(2t)) 2iIm( (e^((iπ)/4) /(t−i))) but (e^((iπ)/4) /(t−i)) = (((t+i) ( ((√2)/2) +i((√2)/2)))/(t^2 +1)) = (1/(t^2 +1)){ ((√2)/2)t +i((√2)/2)t +i((√2)/2) −((√2)/2)) ⇒ Im(...) = (1/(√2)) ((t+1)/(t^2 +1)) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz =−(π/(t^2 +1)) + (π/((√2)(√t))) ((t+1)/(t^2 +1)) = 2f^′ (t) ⇒ f^′ (t) = −(π/(2(t^2 +1))) + (π/(2(√2))) ((t+1)/(t^2 +1)) ⇒ f(t) = −(π/2) ∫_0 ^t (dx/(1+x^2 )) +(π/(2(√2))) ∫_0 ^t ((x+1)/(x^2 +1))dx +c

$${let}\:{f}\left({t}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{arctan}\left({tx}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:{with}\:{t}\geqslant\mathrm{0} \\ $$$${f}^{'} \left({t}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{t}^{\mathrm{2}} \:{x}^{\mathrm{4}} \right)}{dx}\:\Rightarrow \\ $$$$\mathrm{2}{f}^{'} \left({x}\right)=\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{t}^{\mathrm{2}} {x}^{\mathrm{4}} \right)}{dx} \\ $$$${let}\:\varphi\left({z}\right)\:=\:\frac{{z}^{\mathrm{2}} }{\left(\mathrm{1}+{z}^{\mathrm{2}} \right)\left(\mathrm{1}+{t}^{\mathrm{2}} {z}^{\mathrm{4}} \right)} \\ $$$$\varphi\left({z}\right)\:=\:\frac{{z}^{\mathrm{2}} }{\left(\mathrm{1}+{z}^{\mathrm{2}} \right){t}^{\mathrm{2}} \left({z}^{\mathrm{4}} \:+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right)} \\ $$$$=\:\frac{{z}^{\mathrm{2}} }{{t}^{\mathrm{2}} \left({z}−{i}\right)\left({z}+{i}\right)\left({z}^{\mathrm{2}} \:−\frac{{i}}{{t}}\right)\left({z}^{\mathrm{2}} \:+\frac{{i}}{{t}}\right)} \\ $$$$=\:\frac{{z}^{\mathrm{2}} }{{t}^{\mathrm{2}} \left({z}−{i}\right)\left({z}+{i}\right)\left({z}\:−\frac{{e}^{{i}\frac{\pi}{\mathrm{4}}} }{\sqrt{{t}}}\right)\left({z}\:+\frac{{e}^{\frac{{i}\pi}{\mathrm{4}}} }{\sqrt{{t}}}\right)\left({z}−\frac{{e}^{−\frac{{i}\pi}{\mathrm{4}}} }{\sqrt{{t}}}\right)\left({z}+\frac{{e}^{−\frac{{i}\pi}{\mathrm{4}}} }{\sqrt{{t}}}\right)} \\ $$$$\int_{−\infty} ^{+\infty} \:\:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:{Res}\left(\varphi,{i}\right)\:+{Res}\left(\varphi,\frac{{e}^{\frac{{i}\pi}{\mathrm{4}}} }{\sqrt{{t}}}\right)\:+{Res}\left(\varphi,−\frac{{e}^{−\frac{{i}\pi}{\mathrm{4}}} }{\sqrt{{t}}}\right)\right\} \\ $$$${Res}\left(\varphi,{i}\right)\:=\:\:\frac{−\mathrm{1}}{{t}^{\mathrm{2}} \left(\mathrm{2}{i}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right)}\:=\frac{−\mathrm{1}}{\mathrm{2}{i}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$${Res}\left(\varphi,\:\frac{{e}^{\frac{{i}\pi}{\mathrm{4}}} }{\sqrt{{t}}}\right)\:=\:\:\frac{\frac{{i}}{{t}}}{{t}^{\mathrm{2}} \left(\mathrm{1}+\frac{{i}}{{t}}\right)\left(\mathrm{2}\:\frac{{e}^{\frac{{i}\pi}{\mathrm{4}}} }{\sqrt{{t}}}\right)\left(\mathrm{2}\frac{{i}}{{t}}\right)} \\ $$$$=\:\:\frac{{i}}{\mathrm{4}{t}^{\mathrm{3}} \left(\:\frac{{t}+{i}}{{t}}\right)\:\left(\frac{{e}^{\frac{{i}\pi}{\mathrm{4}}} }{\sqrt{{t}}}\right)\:\frac{{i}}{{t}}}\:=\frac{{i}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \sqrt{{t}}}{\mathrm{4}{t}\left({t}+{i}\right){i}}\:\:=\frac{\sqrt{{t}}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} }{\mathrm{4}{t}\left({t}+{i}\right)} \\ $$$${Res}\left(\varphi,−\frac{{e}^{−\frac{{i}\pi}{\mathrm{4}}} }{\sqrt{{t}}}\right)\:=\:\frac{−\frac{{i}}{{t}}}{{t}^{\mathrm{2}} \left(−\frac{{i}}{{t}}\:+\mathrm{1}\right)\left(−\mathrm{2}\:\frac{{e}^{−\frac{{i}\pi}{\mathrm{4}}} }{\sqrt{{t}}}\right)\left(\frac{−\mathrm{2}{i}}{{t}}\right)} \\ $$$$=\:\:\:\frac{−\mathrm{1}}{\mathrm{4}{t}^{\mathrm{3}} \left(\:\frac{−{i}+{t}}{{t}}\right)\:\frac{{e}^{−\frac{{i}\pi}{\mathrm{4}}} }{\sqrt{{t}}}\:\frac{\mathrm{1}}{{t}}}\:\:=\:−\frac{\sqrt{{t}}\:{e}^{\frac{{i}\pi}{\mathrm{4}}} }{\mathrm{4}{t}\left({t}−{i}\right)}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:\:\frac{−\mathrm{1}}{\mathrm{2}{i}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}\:+\frac{\sqrt{{t}}}{\mathrm{4}{t}}\left(\:−\:\frac{{e}^{\frac{{i}\pi}{\mathrm{4}}} }{{t}−{i}}\:+\:\frac{{e}^{−\frac{{i}\pi}{\mathrm{4}}} }{{t}+{i}}\right)\right\} \\ $$$$=\:\frac{−\pi}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\:−\frac{{i}\pi\sqrt{{t}}}{\mathrm{2}{t}}\:\mathrm{2}{iIm}\left(\:\frac{{e}^{\frac{{i}\pi}{\mathrm{4}}} }{{t}−{i}}\right)\:{but} \\ $$$$\:\frac{{e}^{\frac{{i}\pi}{\mathrm{4}}} }{{t}−{i}}\:=\:\frac{\left({t}+{i}\right)\:\left(\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:+{i}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$=\:\frac{\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\left\{\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}{t}\:+{i}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}{t}\:+{i}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)\:\Rightarrow\:{Im}\left(...\right) \\ $$$$=\:\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:\frac{{t}+\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\:\varphi\left({z}\right){dz}\:=−\frac{\pi}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:+\:\frac{\pi}{\sqrt{\mathrm{2}}\sqrt{{t}}}\:\frac{{t}+\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:=\:\mathrm{2}{f}^{'} \left({t}\right)\:\Rightarrow \\ $$$${f}^{'} \left({t}\right)\:=\:−\frac{\pi}{\mathrm{2}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\:+\:\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}\:\frac{{t}+\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$${f}\left({t}\right)\:\:=\:−\frac{\pi}{\mathrm{2}}\:\int_{\mathrm{0}} ^{{t}} \:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }\:+\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}\:\int_{\mathrm{0}} ^{{t}} \:\:\frac{{x}+\mathrm{1}}{{x}^{\mathrm{2}} \:+\mathrm{1}}{dx}\:+{c} \\ $$

Commented by math khazana by abdo last updated on 07/Jul/18

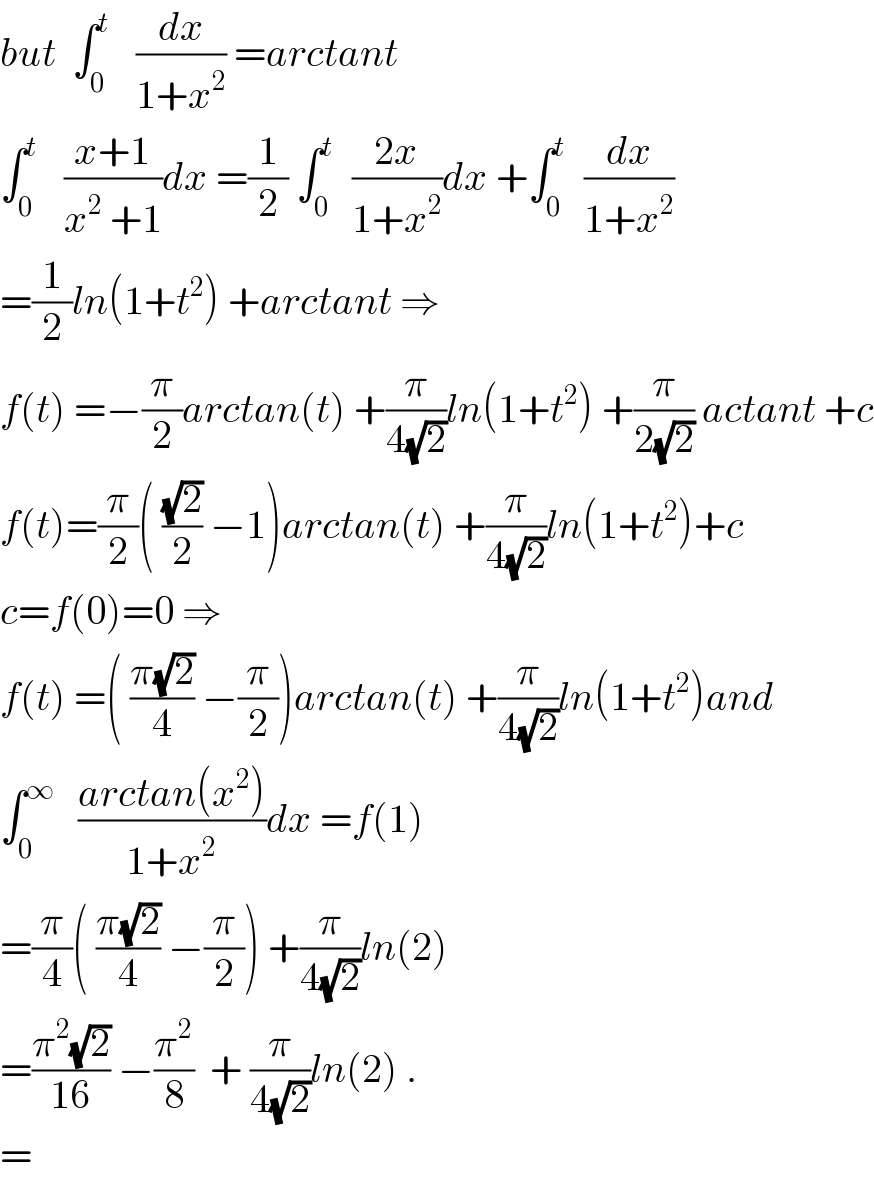
but ∫_0 ^t (dx/(1+x^2 )) =arctant ∫_0 ^t ((x+1)/(x^2 +1))dx =(1/2) ∫_0 ^t ((2x)/(1+x^2 ))dx +∫_0 ^t (dx/(1+x^2 )) =(1/2)ln(1+t^2 ) +arctant ⇒ f(t) =−(π/2)arctan(t) +(π/(4(√2)))ln(1+t^2 ) +(π/(2(√2))) actant +c f(t)=(π/2)( ((√2)/2) −1)arctan(t) +(π/(4(√2)))ln(1+t^2 )+c c=f(0)=0 ⇒ f(t) =( ((π(√2))/4) −(π/2))arctan(t) +(π/(4(√2)))ln(1+t^2 )and ∫_0 ^∞ ((arctan(x^2 ))/(1+x^2 ))dx =f(1) =(π/4)( ((π(√2))/4) −(π/2)) +(π/(4(√2)))ln(2) =((π^2 (√2))/(16)) −(π^2 /8) + (π/(4(√2)))ln(2) . =

$${but}\:\:\int_{\mathrm{0}} ^{{t}} \:\:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }\:={arctant} \\ $$$$\int_{\mathrm{0}} ^{{t}} \:\:\:\frac{{x}+\mathrm{1}}{{x}^{\mathrm{2}} \:+\mathrm{1}}{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{{t}} \:\:\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:+\int_{\mathrm{0}} ^{{t}} \:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\:+{arctant}\:\Rightarrow \\ $$$${f}\left({t}\right)\:=−\frac{\pi}{\mathrm{2}}{arctan}\left({t}\right)\:+\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\:+\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}\:{actant}\:+{c} \\ $$$${f}\left({t}\right)=\frac{\pi}{\mathrm{2}}\left(\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:−\mathrm{1}\right){arctan}\left({t}\right)\:+\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)+{c} \\ $$$${c}={f}\left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow \\ $$$${f}\left({t}\right)\:=\left(\:\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{4}}\:−\frac{\pi}{\mathrm{2}}\right){arctan}\left({t}\right)\:+\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right){and} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{arctan}\left({x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:={f}\left(\mathrm{1}\right) \\ $$$$=\frac{\pi}{\mathrm{4}}\left(\:\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{4}}\:−\frac{\pi}{\mathrm{2}}\right)\:+\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}{ln}\left(\mathrm{2}\right) \\ $$$$=\frac{\pi^{\mathrm{2}} \sqrt{\mathrm{2}}}{\mathrm{16}}\:−\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:\:+\:\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}{ln}\left(\mathrm{2}\right)\:. \\ $$$$= \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com