
Question Number 39402 by ajfour last updated on 06/Jul/18

Commented by ajfour last updated on 06/Jul/18

$${If}\:{the}\:{two}\:{marked}\:{angles}\:{are} \\ $$$${equal},\:\:{find}\:\frac{{r}}{{R}}\:. \\ $$
Answered by MrW3 last updated on 07/Jul/18

Commented by ajfour last updated on 07/Jul/18

$${Thank}\:{you}\:{sir},\:{it}\:{is}\:{with}\:{your} \\ $$$${encouragement}\:{that}\:{i}\:{have} \\ $$$${devised}\:{some}\:{geometry}\:{questions}! \\ $$
Commented by MrW3 last updated on 07/Jul/18
![let λ=(r/R) OC=(√((R−r)^2 −r^2 )) AC=AO+OC=R+(√((R−r)^2 −r^2 )) tan (α/2)=((MC)/(AC))=(r/(R+(√((R−r)^2 −r^2 ))))=(r/(R+(√(R(R−2r))))) ⇒tan (α/2)=(λ/(1+(√(1−2λ)))) ⇒α=2 tan^(−1) (λ/(1+(√(1−2λ)))) BC^2 =AC×(2R−AC)=[R+(√((R−r)^2 −r^2 ))][2R−R−(√((R−r)^2 −r^2 ))] =[R+(√((R−r)^2 −r^2 ))][R−(√((R−r)^2 −r^2 ))] =R^2 −(R−r)^2 +r^2 =2Rr ⇒BC=(√(2Rr)) BM=BC+CM=(√(2Rr))+r sin β=((ME)/(BM))=(r/(r+(√(2Rr)))) ⇒sin β=(λ/(λ+(√(2λ)))) ⇒β=sin^(−1) (λ/(λ+(√(2λ)))) so that α=β: 2 tan^(−1) (λ/(1+(√(1−2λ))))=sin^(−1) (λ/(λ+(√(2λ)))) ⇒λ=(r/R)≈0.2215](Q39528.png)
$${let}\:\lambda=\frac{{r}}{{R}} \\ $$$${OC}=\sqrt{\left({R}−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} } \\ $$$${AC}={AO}+{OC}={R}+\sqrt{\left({R}−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} } \\ $$$$\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}=\frac{{MC}}{{AC}}=\frac{{r}}{{R}+\sqrt{\left({R}−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }}=\frac{{r}}{{R}+\sqrt{{R}\left({R}−\mathrm{2}{r}\right)}} \\ $$$$\Rightarrow\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}=\frac{\lambda}{\mathrm{1}+\sqrt{\mathrm{1}−\mathrm{2}\lambda}} \\ $$$$\Rightarrow\alpha=\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \frac{\lambda}{\mathrm{1}+\sqrt{\mathrm{1}−\mathrm{2}\lambda}} \\ $$$$ \\ $$$${BC}^{\mathrm{2}} ={AC}×\left(\mathrm{2}{R}−{AC}\right)=\left[{R}+\sqrt{\left({R}−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }\right]\left[\mathrm{2}{R}−{R}−\sqrt{\left({R}−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }\right] \\ $$$$=\left[{R}+\sqrt{\left({R}−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }\right]\left[{R}−\sqrt{\left({R}−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }\right] \\ $$$$={R}^{\mathrm{2}} −\left({R}−{r}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} \\ $$$$=\mathrm{2}{Rr} \\ $$$$\Rightarrow{BC}=\sqrt{\mathrm{2}{Rr}} \\ $$$${BM}={BC}+{CM}=\sqrt{\mathrm{2}{Rr}}+{r} \\ $$$$\mathrm{sin}\:\beta=\frac{{ME}}{{BM}}=\frac{{r}}{{r}+\sqrt{\mathrm{2}{Rr}}} \\ $$$$\Rightarrow\mathrm{sin}\:\beta=\frac{\lambda}{\lambda+\sqrt{\mathrm{2}\lambda}} \\ $$$$\Rightarrow\beta=\mathrm{sin}^{−\mathrm{1}} \frac{\lambda}{\lambda+\sqrt{\mathrm{2}\lambda}} \\ $$$$ \\ $$$${so}\:{that}\:\alpha=\beta: \\ $$$$\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \frac{\lambda}{\mathrm{1}+\sqrt{\mathrm{1}−\mathrm{2}\lambda}}=\mathrm{sin}^{−\mathrm{1}} \frac{\lambda}{\lambda+\sqrt{\mathrm{2}\lambda}} \\ $$$$\Rightarrow\lambda=\frac{{r}}{{R}}\approx\mathrm{0}.\mathrm{2215} \\ $$
Commented by ajfour last updated on 07/Jul/18
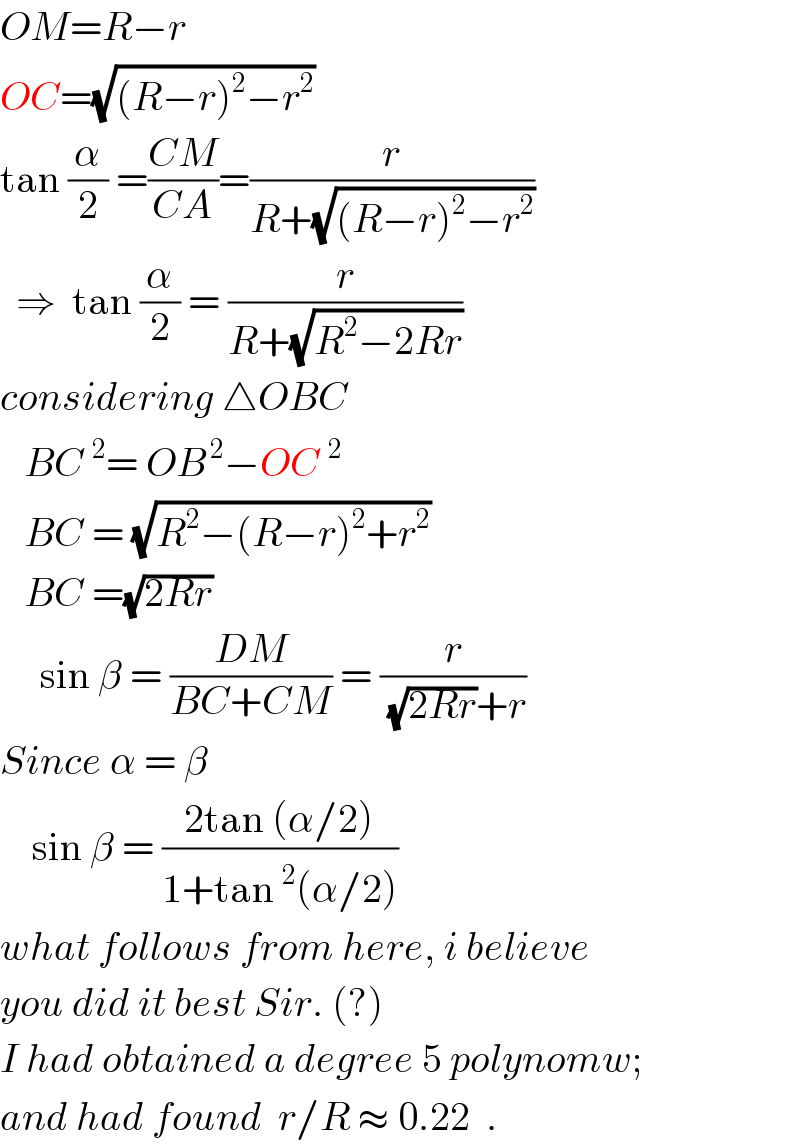
$${OM}={R}−{r} \\ $$$${OC}=\sqrt{\left({R}−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} } \\ $$$$\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}\:=\frac{{CM}}{{CA}}=\frac{{r}}{{R}+\sqrt{\left({R}−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }} \\ $$$$\:\:\Rightarrow\:\:\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}\:=\:\frac{{r}}{{R}+\sqrt{{R}^{\mathrm{2}} −\mathrm{2}{Rr}}} \\ $$$${considering}\:\bigtriangleup{OBC} \\ $$$$\:\:\:{BC}^{\:\:\mathrm{2}} =\:{OB}^{\:\mathrm{2}} −{OC}\:^{\mathrm{2}} \\ $$$$\:\:\:{BC}\:=\:\sqrt{{R}^{\mathrm{2}} −\left({R}−{r}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} } \\ $$$$\:\:\:{BC}\:=\sqrt{\mathrm{2}{Rr}} \\ $$$$\:\:\:\:\:\mathrm{sin}\:\beta\:=\:\frac{{DM}}{{BC}+{CM}}\:=\:\frac{{r}}{\sqrt{\mathrm{2}{Rr}}+{r}} \\ $$$${Since}\:\alpha\:=\:\beta \\ $$$$\:\:\:\:\mathrm{sin}\:\beta\:=\:\frac{\mathrm{2tan}\:\left(\alpha/\mathrm{2}\right)}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \left(\alpha/\mathrm{2}\right)} \\ $$$${what}\:{follows}\:{from}\:{here},\:{i}\:{believe} \\ $$$${you}\:{did}\:{it}\:{best}\:{Sir}.\:\left(?\right) \\ $$$${I}\:{had}\:{obtained}\:{a}\:{degree}\:\mathrm{5}\:{polynomw}; \\ $$$${and}\:{had}\:{found}\:\:{r}/{R}\:\approx\:\mathrm{0}.\mathrm{22}\:\:. \\ $$
Commented by MrW3 last updated on 07/Jul/18

$${Developing}\:{such}\:{interesting}\:{geometry} \\ $$$${questions}\:{requires}\:{deep}\:{understanding} \\ $$$${and}\:{above}\:{all}\:{a}\:{lot}\:{of}\:{phantasy}\:{which} \\ $$$${not}\:{everybody}\:{has}.\:{So}\:{my}\:{respect}! \\ $$
