Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 39404 by ajfour last updated on 06/Jul/18

Commented by ajfour last updated on 06/Jul/18

Q.39365 solution..

$${Q}.\mathrm{39365}\:\:\:{solution}.. \\ $$

Commented by MrW3 last updated on 06/Jul/18

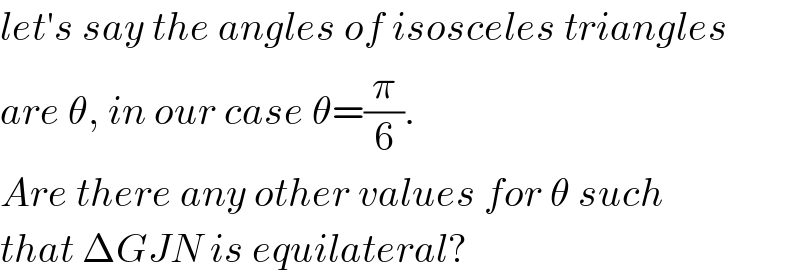
let′s say the angles of isosceles triangles are θ, in our case θ=(π/6). Are there any other values for θ such that ΔGJN is equilateral?

$${let}'{s}\:{say}\:{the}\:{angles}\:{of}\:{isosceles}\:{triangles} \\ $$$${are}\:\theta,\:{in}\:{our}\:{case}\:\theta=\frac{\pi}{\mathrm{6}}. \\ $$$${Are}\:{there}\:{any}\:{other}\:{values}\:{for}\:\theta\:{such} \\ $$$${that}\:\Delta{GJN}\:{is}\:{equilateral}? \\ $$

Commented by behi83417@gmail.com last updated on 06/Jul/18

AG=(b/2)secθ,AN=(c/2)secθ NG^2 =(b^2 /4)sec^2 θ+(c^2 /4)sec^2 θ−((bc)/2)sec^2 θ.cos(60+2θ)= =(1/4)sec^2 θ[b^2 +c^2 −2bc.cos(60+2θ)] NJ^2 =(1/4)sec^2 θ[a^2 +c^2 −2ac.cos(60+2θ)] ⇒a^2 +c^2 −2ac.cos(60+2θ)=b^2 +c^2 −2bc.cos(60+2θ) ⇒a^2 −b^2 =2c(a−b)cos(60+2θ) ⇒^(a≠b) cos(60+2θ)=((a+b)/(2c)) ⇒θ=(1/2)cos^(−1) [((a+b)/(2c))]−30 .

$${AG}=\frac{{b}}{\mathrm{2}}{sec}\theta,{AN}=\frac{{c}}{\mathrm{2}}{sec}\theta \\ $$$${NG}^{\mathrm{2}} =\frac{{b}^{\mathrm{2}} }{\mathrm{4}}{sec}^{\mathrm{2}} \theta+\frac{{c}^{\mathrm{2}} }{\mathrm{4}}{sec}^{\mathrm{2}} \theta−\frac{{bc}}{\mathrm{2}}{sec}^{\mathrm{2}} \theta.{cos}\left(\mathrm{60}+\mathrm{2}\theta\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{sec}^{\mathrm{2}} \theta\left[{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{bc}.{cos}\left(\mathrm{60}+\mathrm{2}\theta\right)\right] \\ $$$${NJ}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}{sec}^{\mathrm{2}} \theta\left[{a}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{ac}.{cos}\left(\mathrm{60}+\mathrm{2}\theta\right)\right] \\ $$$$\Rightarrow{a}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{ac}.{cos}\left(\mathrm{60}+\mathrm{2}\theta\right)={b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{bc}.{cos}\left(\mathrm{60}+\mathrm{2}\theta\right) \\ $$$$\Rightarrow{a}^{\mathrm{2}} −{b}^{\mathrm{2}} =\mathrm{2}{c}\left({a}−{b}\right){cos}\left(\mathrm{60}+\mathrm{2}\theta\right) \\ $$$$\overset{{a}\neq{b}} {\Rightarrow}{cos}\left(\mathrm{60}+\mathrm{2}\theta\right)=\frac{{a}+{b}}{\mathrm{2}{c}} \\ $$$$\Rightarrow\theta=\frac{\mathrm{1}}{\mathrm{2}}{cos}^{−\mathrm{1}} \left[\frac{{a}+{b}}{\mathrm{2}{c}}\right]−\mathrm{30}\:. \\ $$

Commented by MrW3 last updated on 06/Jul/18

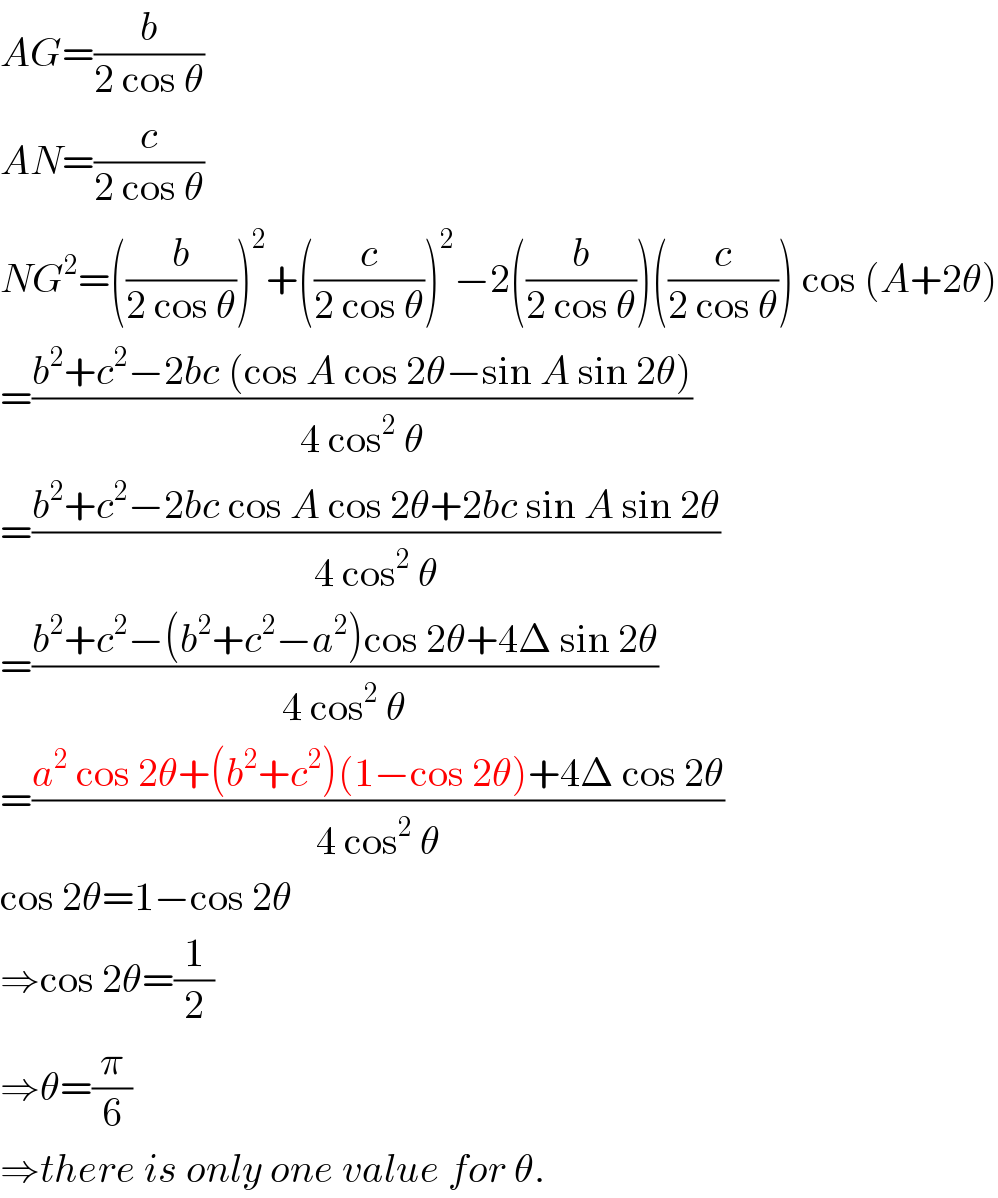
AG=(b/(2 cos θ)) AN=(c/(2 cos θ)) NG^2 =((b/(2 cos θ)))^2 +((c/(2 cos θ)))^2 −2((b/(2 cos θ)))((c/(2 cos θ))) cos (A+2θ) =((b^2 +c^2 −2bc (cos A cos 2θ−sin A sin 2θ))/(4 cos^2 θ)) =((b^2 +c^2 −2bc cos A cos 2θ+2bc sin A sin 2θ)/(4 cos^2 θ)) =((b^2 +c^2 −(b^2 +c^2 −a^2 )cos 2θ+4Δ sin 2θ)/(4 cos^2 θ)) =((a^2 cos 2θ+(b^2 +c^2 )(1−cos 2θ)+4Δ cos 2θ)/(4 cos^2 θ)) cos 2θ=1−cos 2θ ⇒cos 2θ=(1/2) ⇒θ=(π/6) ⇒there is only one value for θ.

$${AG}=\frac{{b}}{\mathrm{2}\:\mathrm{cos}\:\theta} \\ $$$${AN}=\frac{{c}}{\mathrm{2}\:\mathrm{cos}\:\theta} \\ $$$${NG}^{\mathrm{2}} =\left(\frac{{b}}{\mathrm{2}\:\mathrm{cos}\:\theta}\right)^{\mathrm{2}} +\left(\frac{{c}}{\mathrm{2}\:\mathrm{cos}\:\theta}\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{{b}}{\mathrm{2}\:\mathrm{cos}\:\theta}\right)\left(\frac{{c}}{\mathrm{2}\:\mathrm{cos}\:\theta}\right)\:\mathrm{cos}\:\left({A}+\mathrm{2}\theta\right) \\ $$$$=\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{bc}\:\left(\mathrm{cos}\:{A}\:\mathrm{cos}\:\mathrm{2}\theta−\mathrm{sin}\:{A}\:\mathrm{sin}\:\mathrm{2}\theta\right)}{\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$=\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{bc}\:\mathrm{cos}\:{A}\:\mathrm{cos}\:\mathrm{2}\theta+\mathrm{2}{bc}\:\mathrm{sin}\:{A}\:\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$=\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\mathrm{cos}\:\mathrm{2}\theta+\mathrm{4}\Delta\:\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$=\frac{{a}^{\mathrm{2}} \:\mathrm{cos}\:\mathrm{2}\theta+\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta\right)+\mathrm{4}\Delta\:\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$\mathrm{cos}\:\mathrm{2}\theta=\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta \\ $$$$\Rightarrow\mathrm{cos}\:\mathrm{2}\theta=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\theta=\frac{\pi}{\mathrm{6}} \\ $$$$\Rightarrow{there}\:{is}\:{only}\:{one}\:{value}\:{for}\:\theta. \\ $$

Commented by ajfour last updated on 06/Jul/18

marvelous Sir!

$${marvelous}\:{Sir}! \\ $$

Commented by behi83417@gmail.com last updated on 06/Jul/18

dear master!for what? cos2θ=1−cos2θ

$${dear}\:{master}!{for}\:{what}? \\ $$$${cos}\mathrm{2}\theta=\mathrm{1}−{cos}\mathrm{2}\theta \\ $$

Commented by MrW3 last updated on 06/Jul/18

the term a^2 cos 2θ+(b^2 +c^2 )(1−cos 2θ) must be the same for all three sides including b^2 cos 2θ+(c^2 +a^2 )(1−cos 2θ) c^2 cos 2θ+(a^2 +b^2 )(1−cos 2θ) but this is true only when cos 2θ=1−cos 2θ then a^2 cos 2θ+(b^2 +c^2 )(1−cos 2θ) =b^2 cos 2θ+(c^2 +a^2 )(1−cos 2θ) =c^2 cos 2θ+(a^2 +b^2 )(1−cos 2θ) =(a^2 +b^2 +c^2 )cos 2θ and it′s the same for all three sides.

$${the}\:{term}\:{a}^{\mathrm{2}} \:\mathrm{cos}\:\mathrm{2}\theta+\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta\right) \\ $$$${must}\:{be}\:{the}\:{same}\:{for}\:{all}\:{three}\:{sides} \\ $$$${including} \\ $$$${b}^{\mathrm{2}} \:\mathrm{cos}\:\mathrm{2}\theta+\left({c}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta\right) \\ $$$${c}^{\mathrm{2}} \:\mathrm{cos}\:\mathrm{2}\theta+\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta\right) \\ $$$${but}\:{this}\:{is}\:{true}\:{only}\:{when} \\ $$$$\mathrm{cos}\:\mathrm{2}\theta=\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta \\ $$$${then}\: \\ $$$${a}^{\mathrm{2}} \:\mathrm{cos}\:\mathrm{2}\theta+\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta\right) \\ $$$$={b}^{\mathrm{2}} \:\mathrm{cos}\:\mathrm{2}\theta+\left({c}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta\right) \\ $$$$={c}^{\mathrm{2}} \:\mathrm{cos}\:\mathrm{2}\theta+\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta\right) \\ $$$$=\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\mathrm{cos}\:\mathrm{2}\theta \\ $$$${and}\:{it}'{s}\:{the}\:{same}\:{for}\:{all}\:{three}\:{sides}. \\ $$

Answered by ajfour last updated on 06/Jul/18

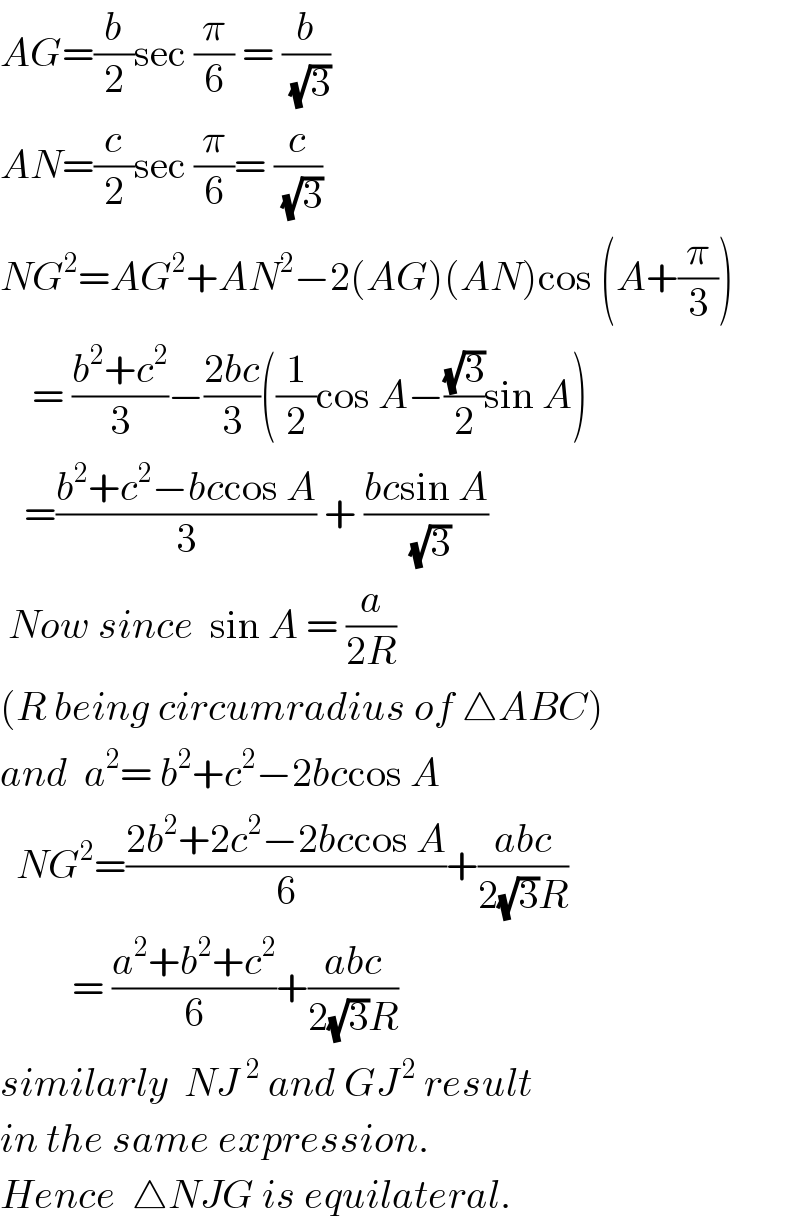
AG=(b/2)sec (π/6) = (b/(√3)) AN=(c/2)sec (π/6)= (c/(√3)) NG^2 =AG^2 +AN^2 −2(AG)(AN)cos (A+(π/3)) = ((b^2 +c^2 )/3)−((2bc)/3)((1/2)cos A−((√3)/2)sin A) =((b^2 +c^2 −bccos A)/3) + ((bcsin A)/(√3)) Now since sin A = (a/(2R)) (R being circumradius of △ABC) and a^2 = b^2 +c^2 −2bccos A NG^2 =((2b^2 +2c^2 −2bccos A)/6)+((abc)/(2(√3)R)) = ((a^2 +b^2 +c^2 )/6)+((abc)/(2(√3)R)) similarly NJ^2 and GJ^( 2) result in the same expression. Hence △NJG is equilateral.

$${AG}=\frac{{b}}{\mathrm{2}}\mathrm{sec}\:\frac{\pi}{\mathrm{6}}\:=\:\frac{{b}}{\sqrt{\mathrm{3}}} \\ $$$${AN}=\frac{{c}}{\mathrm{2}}\mathrm{sec}\:\frac{\pi}{\mathrm{6}}=\:\frac{{c}}{\sqrt{\mathrm{3}}} \\ $$$${NG}^{\mathrm{2}} ={AG}^{\mathrm{2}} +{AN}^{\mathrm{2}} −\mathrm{2}\left({AG}\right)\left({AN}\right)\mathrm{cos}\:\left({A}+\frac{\pi}{\mathrm{3}}\right) \\ $$$$\:\:\:\:=\:\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{3}}−\frac{\mathrm{2}{bc}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:{A}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{sin}\:{A}\right) \\ $$$$\:\:\:=\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{bc}\mathrm{cos}\:{A}}{\mathrm{3}}\:+\:\frac{{bc}\mathrm{sin}\:{A}}{\sqrt{\mathrm{3}}} \\ $$$$\:{Now}\:{since}\:\:\mathrm{sin}\:{A}\:=\:\frac{{a}}{\mathrm{2}{R}} \\ $$$$\left({R}\:{being}\:{circumradius}\:{of}\:\bigtriangleup{ABC}\right) \\ $$$${and}\:\:{a}^{\mathrm{2}} =\:{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{bc}\mathrm{cos}\:{A} \\ $$$$\:\:{NG}^{\mathrm{2}} =\frac{\mathrm{2}{b}^{\mathrm{2}} +\mathrm{2}{c}^{\mathrm{2}} −\mathrm{2}{bc}\mathrm{cos}\:{A}}{\mathrm{6}}+\frac{{abc}}{\mathrm{2}\sqrt{\mathrm{3}}{R}} \\ $$$$\:\:\:\:\:\:\:\:\:=\:\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{6}}+\frac{{abc}}{\mathrm{2}\sqrt{\mathrm{3}}{R}} \\ $$$${similarly}\:\:{NJ}\:^{\mathrm{2}} \:{and}\:{GJ}^{\:\mathrm{2}} \:{result} \\ $$$${in}\:{the}\:{same}\:{expression}. \\ $$$${Hence}\:\:\bigtriangleup{NJG}\:{is}\:{equilateral}. \\ $$

Commented by behi83417@gmail.com last updated on 06/Jul/18

nice proof sir Ajfour.thanks for drawing the perfect figure.

$${nice}\:{proof}\:{sir}\:{Ajfour}.{thanks}\:{for}\: \\ $$$${drawing}\:{the}\:{perfect}\:{figure}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com