
Question and Answers Forum
Question Number 39416 by Rio Mike last updated on 06/Jul/18
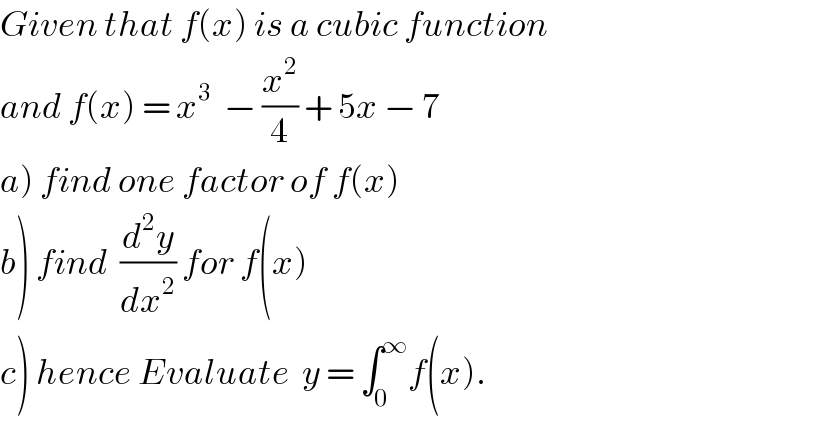
Answered by MJS last updated on 06/Jul/18
![(b) (d^2 y/dx^2 )[f(x)]=f′′(x)=6x−(1/2) (c) ∫f(x)dx=(1/4)x^4 −(1/(12))x^3 +(5/2)x^2 −7x+C ⇒ ∫_0 ^∞ f(x)dx=+∞ (a) what are we allowed to use? approximation procedure with a calculator gives x≈1.15710 Cardano: x^3 −(1/4)x^2 +5x−7=0 z=x+(1/(12)) z^3 +((239)/(48))z−((5689)/(864))=0 u=(1/(12))((5689+24(√(79890))))^(1/3) ; v=(1/(12))((5689−24(√(79890))))^(1/3) z_1 =u+v; x_1 =(1/(12))+u+v≈1.15710 z_2 =(−(1/2)+((√3)/2)i)u+(−(1/2)−((√3)/2)i)v z_2 =(−(1/2)−((√3)/2)i)u+(−(1/2)+((√3)/2)i)v](Q39423.png)
| ||
Question and Answers Forum | ||
Question Number 39416 by Rio Mike last updated on 06/Jul/18 | ||
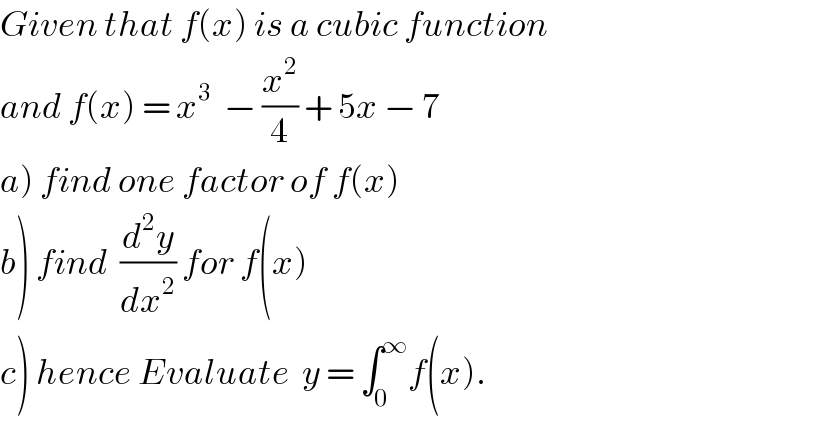 | ||
Answered by MJS last updated on 06/Jul/18 | ||
![(b) (d^2 y/dx^2 )[f(x)]=f′′(x)=6x−(1/2) (c) ∫f(x)dx=(1/4)x^4 −(1/(12))x^3 +(5/2)x^2 −7x+C ⇒ ∫_0 ^∞ f(x)dx=+∞ (a) what are we allowed to use? approximation procedure with a calculator gives x≈1.15710 Cardano: x^3 −(1/4)x^2 +5x−7=0 z=x+(1/(12)) z^3 +((239)/(48))z−((5689)/(864))=0 u=(1/(12))((5689+24(√(79890))))^(1/3) ; v=(1/(12))((5689−24(√(79890))))^(1/3) z_1 =u+v; x_1 =(1/(12))+u+v≈1.15710 z_2 =(−(1/2)+((√3)/2)i)u+(−(1/2)−((√3)/2)i)v z_2 =(−(1/2)−((√3)/2)i)u+(−(1/2)+((√3)/2)i)v](Q39423.png) | ||
| ||