
Question Number 3943 by Rasheed Soomro last updated on 25/Dec/15

$$\mathcal{W}{hat}\:{is}\:{the}\:{area}\:\:{of}\:\:{overlapping}\:{region} \\ $$ $${of}\:{three}\:{circles}\:{of}\:{radii}\:\boldsymbol{\mathrm{r}}_{\mathrm{1}} \:,\:\boldsymbol{\mathrm{r}}_{\mathrm{2}} \:,\:\boldsymbol{\mathrm{r}}_{\mathrm{3}} \:{with}\:{their} \\ $$ $${respective}\:{centres}\:\boldsymbol{\mathrm{C}}_{\mathrm{1}} \:,\:\boldsymbol{\mathrm{C}}_{\mathrm{2}} \:{and}\:\boldsymbol{\mathrm{C}}_{\mathrm{3}} \:{when} \\ $$ $$\boldsymbol{\mathrm{r}}_{\mathrm{1}} +\boldsymbol{\mathrm{r}}_{\mathrm{2}} >\:\boldsymbol{\mathrm{C}}_{\mathrm{1}} \boldsymbol{\mathrm{C}}_{\mathrm{2}} \:\:,\:\:\:\boldsymbol{\mathrm{r}}_{\mathrm{2}} +\boldsymbol{\mathrm{r}}_{\mathrm{3}} >\:\boldsymbol{\mathrm{C}}_{\mathrm{2}} \boldsymbol{\mathrm{C}}_{\mathrm{3}} \:\:{and} \\ $$ $$\boldsymbol{\mathrm{r}}_{\mathrm{3}} +\boldsymbol{\mathrm{r}}_{\mathrm{1}} >\:\boldsymbol{\mathrm{C}}_{\mathrm{3}} \boldsymbol{\mathrm{C}}_{\mathrm{1}} . \\ $$ $${Note}\:{that}\:\boldsymbol{\mathrm{C}}_{\boldsymbol{\mathrm{i}}} \boldsymbol{\mathrm{C}}_{\boldsymbol{\mathrm{j}}} \:{is}\:{the}\:{distance}\:{between}\:{centres} \\ $$ $$\boldsymbol{\mathrm{C}}_{\boldsymbol{\mathrm{i}}\:} {and}\:\:\boldsymbol{\mathrm{C}}_{\boldsymbol{\mathrm{j}}} \:. \\ $$
Commented byYozzii last updated on 26/Dec/15

Commented byYozzii last updated on 26/Dec/15

$${Yes}.\:{I}\:{agree}.\:{Look}\:{at}\:{my}\:{image} \\ $$ $${for}\:{a}\:{better}\:{idea}\:{on}\:{finding}\:{the}\:{full} \\ $$ $${area}. \\ $$
Commented byRasheed Soomro last updated on 26/Dec/15
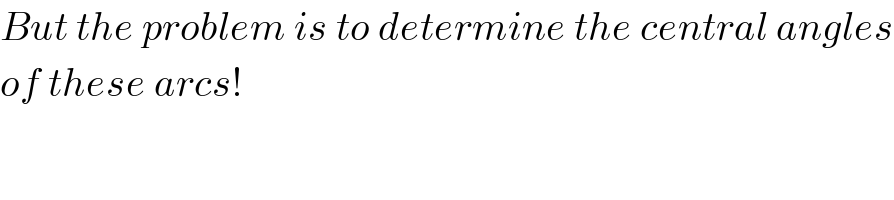
$${But}\:{the}\:{problem}\:{is}\:{to}\:{determine}\:{the}\:{central}\:{angles} \\ $$ $${of}\:{these}\:{arcs}! \\ $$
Commented byYozzii last updated on 25/Dec/15

$${It}\:{is}\:{possible}\:{that}\:{one}\:{circle}\:{completely} \\ $$ $${contains}\:{the}\:{other}\:{two}\:{overlapping} \\ $$ $${circles}.\:{The}\:{problem}\:{then}\:{requires} \\ $$ $${finding}\:{only}\:{the}\:{area}\:{in}\:{which}\:{the} \\ $$ $${two}\:{inner}\:{circles}\:{overlap}\:{since}\:{this} \\ $$ $${same}\:{area}\:{lies}\:{within}\:{the}\:{larger}\: \\ $$ $${circle}.\:{The}\:{conditions}\:{on}\:{r}_{{i}} \:{and}\:{C}_{{i}} {C}_{{j}} \\ $$ $${are}\:{still}\:{satisfied}.\: \\ $$ $$ \\ $$
Commented byYozzii last updated on 25/Dec/15

$${I}\:{think}\:{I}\:{have}\:{a}\:{means}\:{of}\:{finding}\:{the}\:{required} \\ $$ $${area}\:{if}\:{no}\:{two}\:{circles}\:{fully}\:{contain}\:{each}\: \\ $$ $${other}.\:{It}\:{requires}\:{forming}\:{three}\:{new} \\ $$ $${circles}\:{and}\:{a}\:{triangle}.\:{A}\:{diagram}\: \\ $$ $${would}\:{truly}\:{help}\:{my}\:{explanation}.\: \\ $$ $$ \\ $$ $${Suppose}\:{no}\:{two}\:{circles}\:{fully}\:{contain} \\ $$ $${each}\:{other}\:{and}\:{that}\:{they}\:{appear}\:{to}\:{form} \\ $$ $${eight}\:{distinct}\:{regions}\:{in}\:{the}\:{plane}, \\ $$ $${with}\:{the}\:{common}\:{region}\:{of}\:{overlap}\:{having}\:{three} \\ $$ $${vertices}\:{A},{B},{C}.\:{Construct}\:{the}\:{triangle} \\ $$ $${A},{B},{C}.\:{Call}\:{the}\:{area}\:{of}\:\bigtriangleup{ABC}\:\boldsymbol{{A}}_{\mathrm{1}} . \\ $$ $${We}\:{have}\:{AB},{BC}\:{and}\:{CA}\:{as}\:{arcs}, \\ $$ $${because}\:{of}\:{the}\:{manner}\:{in}\:{which}\:{the} \\ $$ $${three}\:{cirvles}\:{overlap},\:{and} \\ $$ $$\:{we}\:{can}\:{form}\:{circles}\:{to}\:{adhere}\:{to} \\ $$ $${each}\:{of}\:{these}\:{arcs}.\:{Thus},\:{if}\:{this}\:{is}\:{done} \\ $$ $${we}\:{can}\:{find}\:{the}\:{respective}\:{areas}\:\boldsymbol{{A}}_{\mathrm{2}} , \\ $$ $$\boldsymbol{{A}}_{\mathrm{3}} \:{and}\:\boldsymbol{{A}}_{\mathrm{4}} ,\:{that}\:{lie}\:{between}\:{each}\:{side} \\ $$ $${of}\:{the}\:{triangle}\:{and}\:{the}\:{arc}\:{opposite}\: \\ $$ $${each}\:{side}.\:{For}\:{a}\:{given}\:{side}\:{with}\:{an}\:{arc}, \\ $$ $${the}\:{area}\:{difference}\:{between}\:{the}\:{sector} \\ $$ $${of}\:{the}\:{circle}\:{with}\:{arc}\:{AB},\:{for}\:{e}.{g},\: \\ $$ $${and}\:{the}\:{isosceles}\:{triangle}\:{ABO}_{\mathrm{1}} , \\ $$ $${where}\:{O}_{\mathrm{1}} \:{is}\:{the}\:{centre}\:{of}\:{this}\:{new}\: \\ $$ $${circle},\:{is}\:\boldsymbol{{A}}_{\mathrm{2}} ,\:{for}\:{example}.\:{The}\:{area}\:{of} \\ $$ $${the}\:{region}\:{of}\:{overlap}\:{is}\:{then}\: \\ $$ $$\boldsymbol{{A}}_{\mathrm{1}} +\boldsymbol{{A}}_{\mathrm{2}} +\boldsymbol{{A}}_{\mathrm{3}} +\boldsymbol{{A}}_{\mathrm{4}} .\: \\ $$ $$ \\ $$
Commented byRasheed Soomro last updated on 25/Dec/15
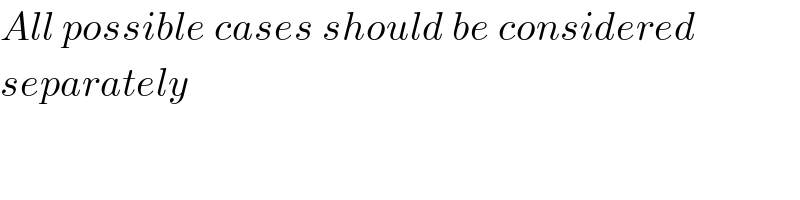
$${All}\:{possible}\:{cases}\:{should}\:{be}\:{considered} \\ $$ $${separately} \\ $$
Commented byYozzii last updated on 25/Dec/15

$${I}\:{just}\:{realized}\:{that}\:{you}\:{only}\:{need}\:{the} \\ $$ $${three}\:{initial}\:{circles}\:{to}\:{do}\:{the} \\ $$ $${calculation}.\:{The}\:{new}\:{circles}\:{I}\:{speak}\:{of} \\ $$ $${only}\:{need}\:{to}\:{be}\:{the}\:{initial}\:{circles}\:{we}\: \\ $$ $${started}\:{with}!\:\left({Waste}\:{of}\:{energy}...\right) \\ $$
Commented byRasheed Soomro last updated on 25/Dec/15
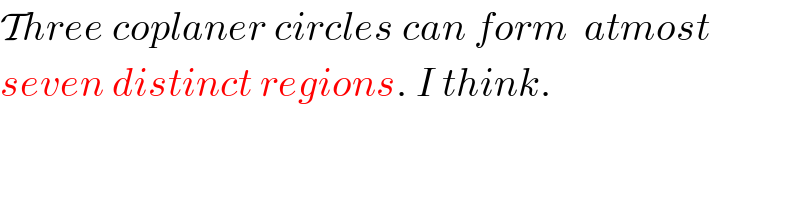
$$\mathcal{T}{hree}\:{coplaner}\:{circles}\:{can}\:{form}\:\:{atmost} \\ $$ $${seven}\:{distinct}\:{regions}.\:{I}\:{think}. \\ $$
Commented byYozzii last updated on 25/Dec/15
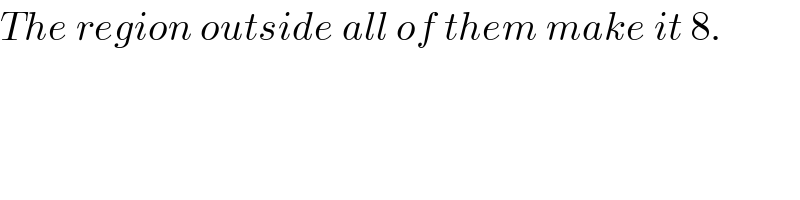
$${The}\:{region}\:{outside}\:{all}\:{of}\:{them}\:{make}\:{it}\:\mathrm{8}. \\ $$
Commented byRasheed Soomro last updated on 26/Dec/15

$${You}\:\:{should}\:{start}\:{with}\:\mathrm{7}−{region}\: \\ $$ $${case}\:,\:{I}\:{think}. \\ $$ $${I}\:{also}\:\:{think}\:{that}\:{the}\:{area}\:{of}\:{overlapping}\:{region}\:{is}\:{closely}/{direcly} \\ $$ $${related}\:{to}\:{the}\:{quantities}:\: \\ $$ $$\boldsymbol{\mathrm{r}}_{\mathrm{1}} +\boldsymbol{\mathrm{r}}_{\mathrm{2}} −\boldsymbol{\mathrm{C}}_{\mathrm{1}} \boldsymbol{\mathrm{C}}_{\mathrm{2}} \:,\:\boldsymbol{\mathrm{r}}_{\mathrm{2}} +\boldsymbol{\mathrm{r}}_{\mathrm{3}} −\boldsymbol{\mathrm{C}}_{\mathrm{2}} \boldsymbol{\mathrm{C}}_{\mathrm{3}} \:,\:\boldsymbol{\mathrm{r}}_{\mathrm{3}} +\boldsymbol{\mathrm{r}}_{\mathrm{1}} −\boldsymbol{\mathrm{C}}_{\mathrm{3}} \boldsymbol{\mathrm{C}}_{\mathrm{1}} \\ $$ $${More}\:{the}\:{circles}\:{are}\:{closed}\:{greater}\:{the}\:{area}\: \\ $$ $${of}\:{overlapping}\:{region}. \\ $$
Commented byYozzii last updated on 26/Dec/15

$${A},{C}\:\&{E}\:{are}\:{circle}\:{centres}.\:{To}\:{find} \\ $$ $${the}\:{area}\:{between}\:{the}\:{arc}\:{HI}\:{and}\:{the} \\ $$ $${chord}\:{HI},\:{find}\:{the}\:{area}\:{of}\:\bigtriangleup{CHI} \\ $$ $${and}\:{then}\:{the}\:{area}\:{of}\:{the}\:{sector} \\ $$ $${CHI}.\:{The}\:{positive}\:{difference}\:{between} \\ $$ $${the}\:{two}\:{areas}\:{gives}\:{what}\:{we}'{re}\: \\ $$ $${searching}\:{for}.\:{This}\:{is}\:{similarly} \\ $$ $${done}\:{for}\:{sector}\:{EGH}\:{and}\:{sector}\:{AGI}. \\ $$ $$ \\ $$
