Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 39436 by ajfour last updated on 06/Jul/18

Commented by ajfour last updated on 06/Jul/18

Commented by ajfour last updated on 06/Jul/18

3φ = 90° ⇒ φ=30° Rsin 30° = asin θ ⇒ sin θ = (R/(2a)) ⇒ cos θ = ((√(4a^2 −R^2 ))/(2a)) bsin (180°−2φ−θ)=(R/2) ⇒ bsin (60°+θ)=(R/2) b = (R/(2[((√3)/2)cos θ+((sin θ)/2)])) =(R/((√3)(((√(4a^2 −R^2 ))/(2a)))+(R/(2a)))) ⇒ b = ((2aR)/(R+(√(12a^2 −3R^2 )))) .

$$\mathrm{3}\phi\:=\:\mathrm{90}°\:\:\:\Rightarrow\:\:\phi=\mathrm{30}° \\ $$$${R}\mathrm{sin}\:\mathrm{30}°\:=\:{a}\mathrm{sin}\:\theta \\ $$$$\Rightarrow\:\:\:\mathrm{sin}\:\theta\:=\:\frac{{R}}{\mathrm{2}{a}}\:\:\Rightarrow\:\mathrm{cos}\:\theta\:=\:\frac{\sqrt{\mathrm{4}{a}^{\mathrm{2}} −{R}^{\mathrm{2}} }}{\mathrm{2}{a}} \\ $$$${b}\mathrm{sin}\:\left(\mathrm{180}°−\mathrm{2}\phi−\theta\right)=\frac{{R}}{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\:{b}\mathrm{sin}\:\left(\mathrm{60}°+\theta\right)=\frac{{R}}{\mathrm{2}} \\ $$$$\:\:\:\boldsymbol{{b}}\:=\:\frac{\boldsymbol{{R}}}{\mathrm{2}\left[\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{cos}\:\theta+\frac{\mathrm{sin}\:\theta}{\mathrm{2}}\right]} \\ $$$$\:\:\:\:\:\:=\frac{{R}}{\sqrt{\mathrm{3}}\left(\frac{\sqrt{\mathrm{4}{a}^{\mathrm{2}} −{R}^{\mathrm{2}} }}{\mathrm{2}{a}}\right)+\frac{{R}}{\mathrm{2}{a}}} \\ $$$$\Rightarrow\:\:{b}\:=\:\frac{\mathrm{2}{aR}}{{R}+\sqrt{\mathrm{12}{a}^{\mathrm{2}} −\mathrm{3}{R}^{\mathrm{2}} }}\:. \\ $$

Answered by MJS last updated on 06/Jul/18

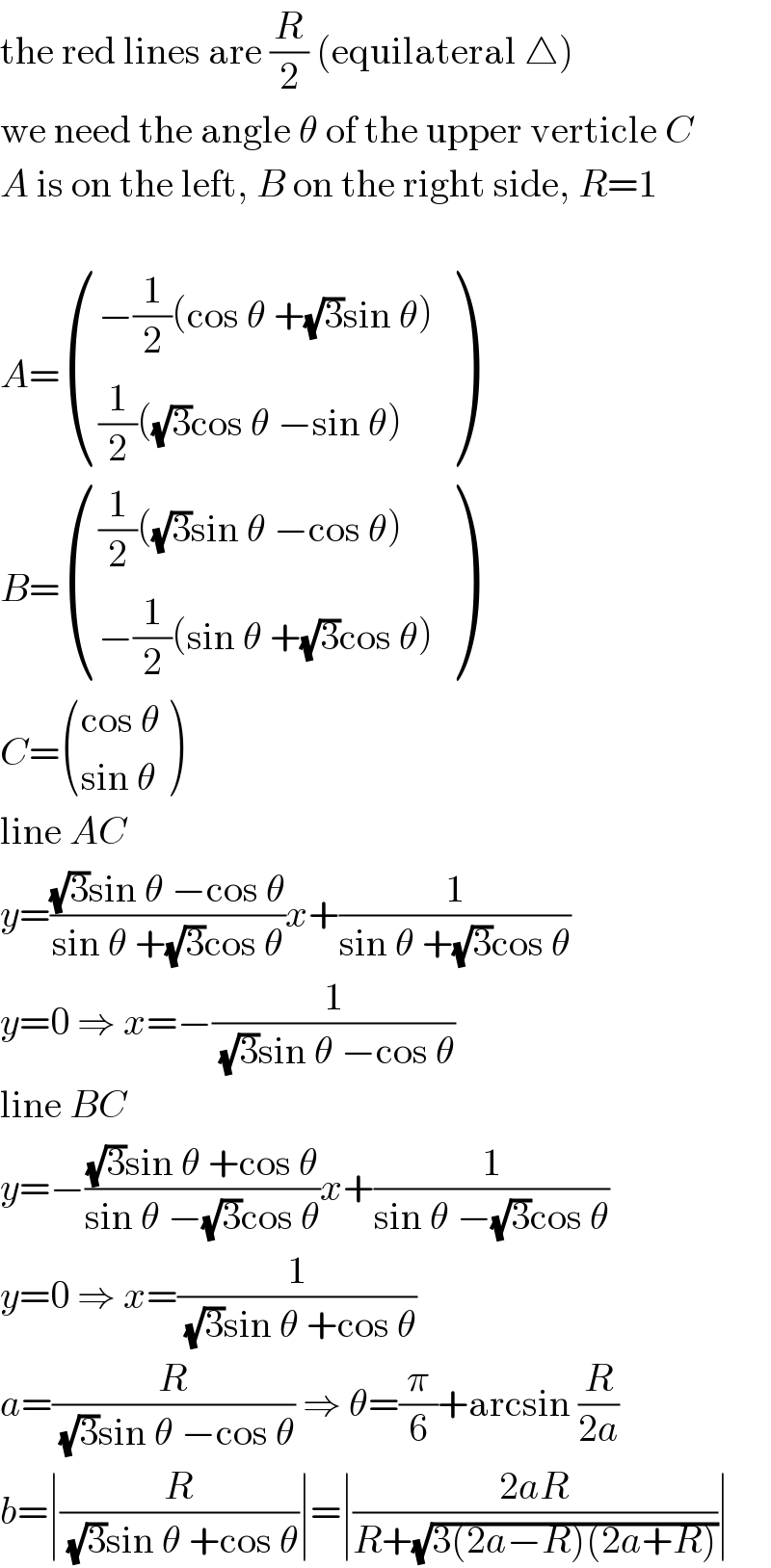
the red lines are (R/2) (equilateral △) we need the angle θ of the upper verticle C A is on the left, B on the right side, R=1 A= (((−(1/2)(cos θ +(√3)sin θ))),(((1/2)((√3)cos θ −sin θ))) ) B= ((((1/2)((√3)sin θ −cos θ))),((−(1/2)(sin θ +(√3)cos θ))) ) C= (((cos θ)),((sin θ)) ) line AC y=(((√3)sin θ −cos θ)/(sin θ +(√3)cos θ))x+(1/(sin θ +(√3)cos θ)) y=0 ⇒ x=−(1/((√3)sin θ −cos θ)) line BC y=−(((√3)sin θ +cos θ)/(sin θ −(√3)cos θ))x+(1/(sin θ −(√3)cos θ)) y=0 ⇒ x=(1/((√3)sin θ +cos θ)) a=(R/((√3)sin θ −cos θ)) ⇒ θ=(π/6)+arcsin (R/(2a)) b=∣(R/((√3)sin θ +cos θ))∣=∣((2aR)/(R+(√(3(2a−R)(2a+R)))))∣

$$\mathrm{the}\:\mathrm{red}\:\mathrm{lines}\:\mathrm{are}\:\frac{{R}}{\mathrm{2}}\:\left(\mathrm{equilateral}\:\bigtriangleup\right) \\ $$$$\mathrm{we}\:\mathrm{need}\:\mathrm{the}\:\mathrm{angle}\:\theta\:\mathrm{of}\:\mathrm{the}\:\mathrm{upper}\:\mathrm{verticle}\:{C} \\ $$$${A}\:\mathrm{is}\:\mathrm{on}\:\mathrm{the}\:\mathrm{left},\:{B}\:\mathrm{on}\:\mathrm{the}\:\mathrm{right}\:\mathrm{side},\:{R}=\mathrm{1} \\ $$$$ \\ $$$${A}=\begin{pmatrix}{−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}\:\theta\:+\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\right)}\\{\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\mathrm{3}}\mathrm{cos}\:\theta\:−\mathrm{sin}\:\theta\right)}\end{pmatrix} \\ $$$${B}=\begin{pmatrix}{\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\:−\mathrm{cos}\:\theta\right)}\\{−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{sin}\:\theta\:+\sqrt{\mathrm{3}}\mathrm{cos}\:\theta\right)}\end{pmatrix} \\ $$$${C}=\begin{pmatrix}{\mathrm{cos}\:\theta}\\{\mathrm{sin}\:\theta}\end{pmatrix} \\ $$$$\mathrm{line}\:{AC} \\ $$$${y}=\frac{\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\:−\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta\:+\sqrt{\mathrm{3}}\mathrm{cos}\:\theta}{x}+\frac{\mathrm{1}}{\mathrm{sin}\:\theta\:+\sqrt{\mathrm{3}}\mathrm{cos}\:\theta} \\ $$$${y}=\mathrm{0}\:\Rightarrow\:{x}=−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\:−\mathrm{cos}\:\theta} \\ $$$$\mathrm{line}\:{BC} \\ $$$${y}=−\frac{\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\:+\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta\:−\sqrt{\mathrm{3}}\mathrm{cos}\:\theta}{x}+\frac{\mathrm{1}}{\mathrm{sin}\:\theta\:−\sqrt{\mathrm{3}}\mathrm{cos}\:\theta} \\ $$$${y}=\mathrm{0}\:\Rightarrow\:{x}=\frac{\mathrm{1}}{\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\:+\mathrm{cos}\:\theta} \\ $$$${a}=\frac{{R}}{\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\:−\mathrm{cos}\:\theta}\:\Rightarrow\:\theta=\frac{\pi}{\mathrm{6}}+\mathrm{arcsin}\:\frac{{R}}{\mathrm{2}{a}} \\ $$$${b}=\mid\frac{{R}}{\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\:+\mathrm{cos}\:\theta}\mid=\mid\frac{\mathrm{2}{aR}}{{R}+\sqrt{\mathrm{3}\left(\mathrm{2}{a}−{R}\right)\left(\mathrm{2}{a}+{R}\right)}}\mid \\ $$

Commented by ajfour last updated on 06/Jul/18

Thank you Sir, i got the same.

$${Thank}\:{you}\:{Sir},\:{i}\:{got}\:{the}\:{same}. \\ $$

Commented by MJS last updated on 06/Jul/18

yes Sir. you′re an angler, I catch the fish in a net of coordinates ;−)

$$\mathrm{yes}\:\mathrm{Sir}.\:\mathrm{you}'\mathrm{re}\:\mathrm{an}\:\mathrm{angler},\:\mathrm{I}\:\mathrm{catch}\:\mathrm{the}\:\mathrm{fish}\:\mathrm{in} \\ $$$$\left.\mathrm{a}\:\mathrm{net}\:\mathrm{of}\:\mathrm{coordinates}\:;−\right) \\ $$

Commented by Rasheed.Sindhi last updated on 07/Jul/18

Good anology! Really coordinate system is a net and an angler doesn′t use net for fishing!

$$\mathcal{G}{ood}\:{anology}!\:\mathrm{Really}\:\mathrm{coordinate}\:\mathrm{system} \\ $$$$\mathrm{is}\:\mathrm{a}\:\mathrm{net}\:\mathrm{and}\:\mathrm{an}\:\mathrm{angler}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{use}\:\mathrm{net} \\ $$$$\mathrm{for}\:\mathrm{fishing}! \\ $$

Commented by behi83417@gmail.com last updated on 06/Jul/18

sir rasheed! Q#39298 whaits for you.

$${sir}\:{rasheed}!\:{Q}#\mathrm{39298}\:{whaits}\:{for}\:{you}. \\ $$

Commented by Rasheed.Sindhi last updated on 07/Jul/18

Too hard for me!

$$\mathrm{Too}\:\mathrm{hard}\:\mathrm{for}\:\mathrm{me}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com