Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 39443 by rahul 19 last updated on 06/Jul/18

lim_(n→∞) [ (1/(n^2 +1))+ (2/(n^2 +2))+ (3/(n^2 +3))+ ....+(1/(n+1))] = ?

$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\left[\:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} +\mathrm{1}}+\:\frac{\mathrm{2}}{\mathrm{n}^{\mathrm{2}} +\mathrm{2}}+\:\frac{\mathrm{3}}{\mathrm{n}^{\mathrm{2}} +\mathrm{3}}+\:....+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\right]\:=\:? \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 06/Jul/18

very good...this is the way to solve it...

$${very}\:{good}...{this}\:{is}\:{the}\:{way}\:{to}\:{solve}\:{it}... \\ $$

Commented by math khazana by abdo last updated on 06/Jul/18

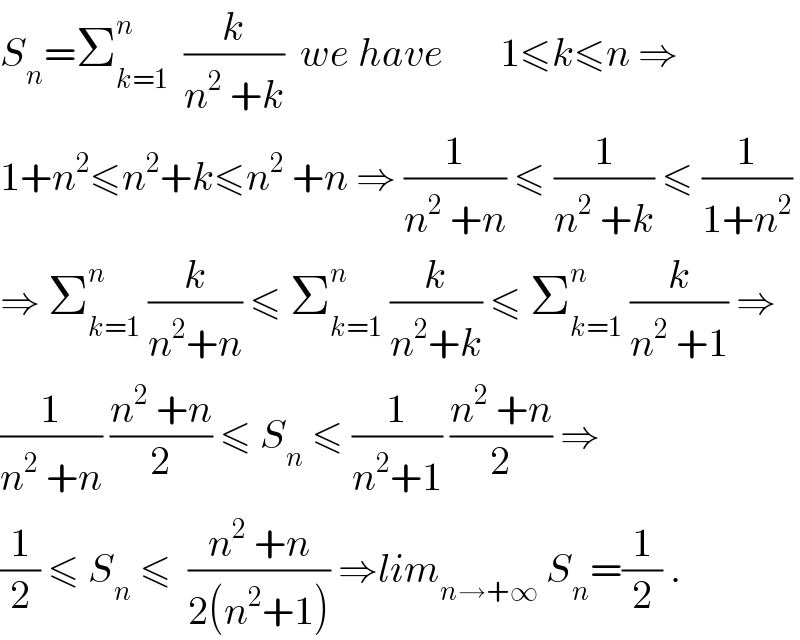
S_n =Σ_(k=1) ^n (k/(n^2 +k)) we have 1≤k≤n ⇒ 1+n^2 ≤n^2 +k≤n^2 +n ⇒ (1/(n^2 +n)) ≤ (1/(n^2 +k)) ≤ (1/(1+n^2 )) ⇒ Σ_(k=1) ^n (k/(n^2 +n)) ≤ Σ_(k=1) ^n (k/(n^2 +k)) ≤ Σ_(k=1) ^n (k/(n^2 +1)) ⇒ (1/(n^2 +n)) ((n^2 +n)/2) ≤ S_n ≤ (1/(n^2 +1)) ((n^2 +n)/2) ⇒ (1/2) ≤ S_n ≤ ((n^2 +n)/(2(n^2 +1))) ⇒lim_(n→+∞) S_n =(1/2) .

$${S}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{{k}}{{n}^{\mathrm{2}} \:+{k}}\:\:{we}\:{have}\:\:\:\:\:\:\:\mathrm{1}\leqslant{k}\leqslant{n}\:\Rightarrow \\ $$$$\mathrm{1}+{n}^{\mathrm{2}} \leqslant{n}^{\mathrm{2}} +{k}\leqslant{n}^{\mathrm{2}} \:+{n}\:\Rightarrow\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} \:+{n}}\:\leqslant\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} \:+{k}}\:\leqslant\:\frac{\mathrm{1}}{\mathrm{1}+{n}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{{k}}{{n}^{\mathrm{2}} +{n}}\:\leqslant\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{{k}}{{n}^{\mathrm{2}} +{k}}\:\leqslant\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{{k}}{{n}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{{n}^{\mathrm{2}} \:+{n}}\:\frac{{n}^{\mathrm{2}} \:+{n}}{\mathrm{2}}\:\leqslant\:{S}_{{n}} \:\leqslant\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} +\mathrm{1}}\:\frac{{n}^{\mathrm{2}} \:+{n}}{\mathrm{2}}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:\leqslant\:{S}_{{n}} \:\leqslant\:\:\frac{{n}^{\mathrm{2}} \:+{n}}{\mathrm{2}\left({n}^{\mathrm{2}} +\mathrm{1}\right)}\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\:. \\ $$

Commented by abdo mathsup 649 cc last updated on 07/Jul/18

thanks.

$${thanks}. \\ $$

Answered by ajfour last updated on 06/Jul/18

Let n^2 =N L=lim_(N→∞) NΣ_(r=1) ^(√N) (((r/N)((1/N)))/(1+(r/N))) =lim_(N→∞) N∫_0 ^( 1/(√N)) ((xdx)/(1+x)) =lim_(N→∞) N[(1/(√N))−ln (1+(1/(√N)))] =lim_(N→∞) N[(1/(√N))−(1/(√N))+(1/(2N))−....] ⇒ L = (1/2) .

$${Let}\:{n}^{\mathrm{2}} ={N} \\ $$$${L}=\underset{{N}\rightarrow\infty} {\mathrm{lim}}{N}\underset{{r}=\mathrm{1}} {\overset{\sqrt{{N}}} {\sum}}\:\frac{\left({r}/{N}\right)\left(\frac{\mathrm{1}}{{N}}\right)}{\mathrm{1}+\frac{{r}}{{N}}} \\ $$$$\:\:\:=\underset{{N}\rightarrow\infty} {\mathrm{lim}}{N}\int_{\mathrm{0}} ^{\:\:\mathrm{1}/\sqrt{{N}}} \:\frac{{xdx}}{\mathrm{1}+{x}} \\ $$$$\:\:=\underset{{N}\rightarrow\infty} {\mathrm{lim}}{N}\left[\frac{\mathrm{1}}{\sqrt{{N}}}−\mathrm{ln}\:\left(\mathrm{1}+\frac{\mathrm{1}}{\sqrt{{N}}}\right)\right] \\ $$$$\:\:=\underset{{N}\rightarrow\infty} {\mathrm{lim}}\:{N}\left[\frac{\mathrm{1}}{\sqrt{{N}}}−\frac{\mathrm{1}}{\sqrt{{N}}}+\frac{\mathrm{1}}{\mathrm{2}{N}}−....\right] \\ $$$$\Rightarrow\:\:\:\:\:{L}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:. \\ $$

Commented by rahul 19 last updated on 06/Jul/18

Ans. given is 1/2

Terms of Service

Privacy Policy

Contact: info@tinkutara.com