Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 39508 by behi83417@gmail.com last updated on 06/Jul/18

Commented by behi83417@gmail.com last updated on 06/Jul/18

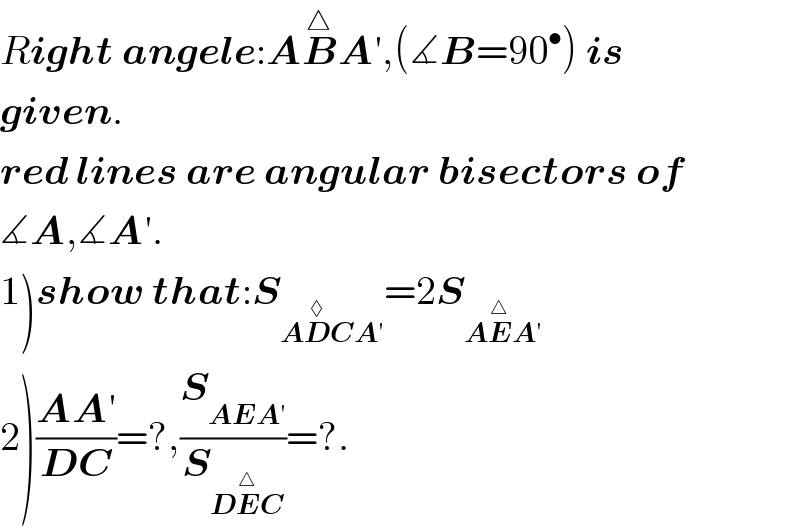
Right angele:AB^△ A′,(∡B=90^• ) is given. red lines are angular bisectors of ∡A,∡A′. 1)show that:S_(AD^◊ CA′) =2S_(AE^△ A′) 2)((AA′)/(DC))=?,(S_(AEA′) /S_(DE^△ C) )=?.

$${R}\boldsymbol{{ight}}\:\boldsymbol{{angele}}:\boldsymbol{{A}}\overset{\bigtriangleup} {\boldsymbol{{B}A}}',\left(\measuredangle\boldsymbol{{B}}=\mathrm{90}^{\bullet} \right)\:\boldsymbol{{is}} \\ $$$$\boldsymbol{{given}}. \\ $$$$\boldsymbol{{red}}\:\boldsymbol{{lines}}\:\boldsymbol{{are}}\:\boldsymbol{{angular}}\:\boldsymbol{{bisectors}}\:\boldsymbol{{of}} \\ $$$$\measuredangle\boldsymbol{{A}},\measuredangle\boldsymbol{{A}}'. \\ $$$$\left.\mathrm{1}\right)\boldsymbol{{show}}\:\boldsymbol{{that}}:\boldsymbol{{S}}_{\boldsymbol{{A}}\overset{\lozenge} {\boldsymbol{{D}CA}}'} =\mathrm{2}\boldsymbol{{S}}_{\boldsymbol{{A}}\overset{\bigtriangleup} {\boldsymbol{{E}A}}'} \\ $$$$\left.\mathrm{2}\right)\frac{\boldsymbol{{AA}}'}{\boldsymbol{{DC}}}=?,\frac{\boldsymbol{{S}}_{\boldsymbol{{AEA}}'} }{\boldsymbol{{S}}_{\boldsymbol{{D}}\overset{\bigtriangleup} {\boldsymbol{{E}C}}} }=?. \\ $$

Answered by MrW3 last updated on 07/Jul/18

Commented by MrW3 last updated on 07/Jul/18

∠A′+∠A=90° A′C′=A′C AD′=AD ⇒C′E=CE, D′E=DE ∠CED=∠A′EA=180°−((∠A′)/2)−((∠A)/2)=135° α=180°−135°=45° ∠C′ED′=135°−2α=45° A_(ΔCED) =(1/2)×CE×DE×sin ∠CED A_(ΔC′ED′) =(1/2)×C′E×D′E×sin ∠C′ED′ =(1/2)×CE×DE×sin 45° =(1/2)×CE×DE×sin 135° =(1/2)×CE×DE×sin ∠CED =A_(ΔCED) A_(ΔA′EA) =A_(ΔA′EC′) +A_(ΔC′ED′) +A_(ΔD′EA) =A_(ΔA′EC) +A_(ΔCED) +A_(ΔDEA) A_(A′CDA) =A_(ΔA′EA) +A_(ΔA′EC) +A_(ΔCED) +A_(ΔDEA) =2A_(ΔA′EA)

$$\angle{A}'+\angle{A}=\mathrm{90}° \\ $$$${A}'{C}'={A}'{C} \\ $$$${AD}'={AD} \\ $$$$\Rightarrow{C}'{E}={CE},\:{D}'{E}={DE} \\ $$$$\angle{CED}=\angle{A}'{EA}=\mathrm{180}°−\frac{\angle{A}'}{\mathrm{2}}−\frac{\angle{A}}{\mathrm{2}}=\mathrm{135}° \\ $$$$\alpha=\mathrm{180}°−\mathrm{135}°=\mathrm{45}° \\ $$$$\angle{C}'{ED}'=\mathrm{135}°−\mathrm{2}\alpha=\mathrm{45}° \\ $$$${A}_{\Delta{CED}} =\frac{\mathrm{1}}{\mathrm{2}}×{CE}×{DE}×\mathrm{sin}\:\angle{CED} \\ $$$${A}_{\Delta{C}'{ED}'} =\frac{\mathrm{1}}{\mathrm{2}}×{C}'{E}×{D}'{E}×\mathrm{sin}\:\angle{C}'{ED}' \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×{CE}×{DE}×\mathrm{sin}\:\mathrm{45}° \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×{CE}×{DE}×\mathrm{sin}\:\mathrm{135}° \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×{CE}×{DE}×\mathrm{sin}\:\angle{CED} \\ $$$$={A}_{\Delta{CED}} \\ $$$${A}_{\Delta{A}'{EA}} ={A}_{\Delta{A}'{EC}'} +{A}_{\Delta{C}'{ED}'} +{A}_{\Delta{D}'{EA}} \\ $$$$={A}_{\Delta{A}'{EC}} +{A}_{\Delta{CED}} +{A}_{\Delta{DEA}} \\ $$$${A}_{{A}'{CDA}} ={A}_{\Delta{A}'{EA}} +{A}_{\Delta{A}'{EC}} +{A}_{\Delta{CED}} +{A}_{\Delta{DEA}} \\ $$$$=\mathrm{2}{A}_{\Delta{A}'{EA}} \\ $$

Commented by behi83417@gmail.com last updated on 07/Jul/18

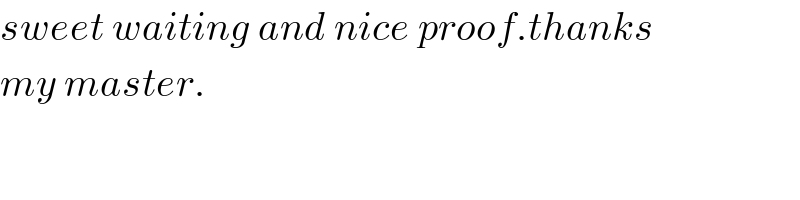
sweet waiting and nice proof.thanks my master.

$${sweet}\:{waiting}\:{and}\:{nice}\:{proof}.{thanks} \\ $$$${my}\:{master}. \\ $$

Commented by behi83417@gmail.com last updated on 07/Jul/18

perpendicular from :E to AA′,say:EH. S_(AEA′) =(1/2).EH.AA′=(1/2).r.b [r=radius of incircle of AB^△ A′.] ((sin(A/2))/(A′C))=((sinACA′)/b),((sin(A/2))/(BC))=((sinACB)/c) (b/(A′C))=(c/(BC))⇒((A′C)/(BC))=(b/c)⇒((A′C)/a)=(b/(b+c)) ⇒A′C=((ab)/(b+c)),BC=((ac)/(b+c)),BD=((ca)/(b+a)),AD=((cb)/(b+a)) S_(ADCA′) =S_(ABA′) −S_(DBC) =(1/2)ac−(1/2)BD.BC= =(1/2)ac−(1/2).((ac)/(a+b)).((ac)/(b+c))=((ac)/2)(1−((ac)/((a+b)(b+c))))= =((ac)/2)(((ab+ac+b^2 +bc−ac)/((a+b)(b+c))))=((ac)/2).((b^2 +ab+bc)/((a+b)(b+c)))= =((ac)/2).((a^2 +c^2 +b^2 +2ba+2bc)/(2(a+b)(b+c)))=((ac)/2).(((a+b+c)^2 −2ac)/(2ab+2ac+2b^2 +2bc))= =S.(((2p)^2 −4S)/((2p)^2 ))=S.((p^2 −S)/p^2 )=S−(S^2 /p^2 )=S−r^2 = =r.p−r^2 =r.(p−r)=r.b=2S_(AEA′) . ■ note:in right angle triangle:b=p−r because: p−r=p−(S/p)=((p^2 −S)/p)= =(((a+b+c)^2 −2ac)/(4p))=((a^2 +b^2 +c^2 +2ab+2bc)/(4p)) =((2b^2 +2ba+2bc)/(4p))=((2b(a+b+c))/(4p))=((2b.2p)/(4p))=b.

$${perpendicular}\:{from}\::{E}\:{to}\:{AA}',{say}:{EH}. \\ $$$${S}_{{AEA}'} =\frac{\mathrm{1}}{\mathrm{2}}.{EH}.{AA}'=\frac{\mathrm{1}}{\mathrm{2}}.{r}.{b} \\ $$$$\left[\boldsymbol{{r}}=\boldsymbol{{radius}}\:\boldsymbol{{of}}\:\boldsymbol{{incircle}}\:\boldsymbol{{of}}\:\boldsymbol{{A}}\overset{\bigtriangleup} {\boldsymbol{{B}A}}'.\right] \\ $$$$\frac{{sin}\frac{{A}}{\mathrm{2}}}{{A}'{C}}=\frac{{sinACA}'}{{b}},\frac{{sin}\frac{{A}}{\mathrm{2}}}{{BC}}=\frac{{sinACB}}{{c}} \\ $$$$\frac{{b}}{{A}'{C}}=\frac{{c}}{{BC}}\Rightarrow\frac{{A}'{C}}{{BC}}=\frac{{b}}{{c}}\Rightarrow\frac{{A}'{C}}{{a}}=\frac{{b}}{{b}+{c}} \\ $$$$\Rightarrow{A}'{C}=\frac{{ab}}{{b}+{c}},{BC}=\frac{{ac}}{{b}+{c}},{BD}=\frac{{ca}}{{b}+{a}},{AD}=\frac{{cb}}{{b}+{a}} \\ $$$${S}_{{ADCA}'} ={S}_{{ABA}'} −{S}_{{DBC}} =\frac{\mathrm{1}}{\mathrm{2}}{ac}−\frac{\mathrm{1}}{\mathrm{2}}{BD}.{BC}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ac}−\frac{\mathrm{1}}{\mathrm{2}}.\frac{{ac}}{{a}+{b}}.\frac{{ac}}{{b}+{c}}=\frac{{ac}}{\mathrm{2}}\left(\mathrm{1}−\frac{{ac}}{\left({a}+{b}\right)\left({b}+{c}\right)}\right)= \\ $$$$=\frac{{ac}}{\mathrm{2}}\left(\frac{{ab}+{ac}+{b}^{\mathrm{2}} +{bc}−{ac}}{\left({a}+{b}\right)\left({b}+{c}\right)}\right)=\frac{{ac}}{\mathrm{2}}.\frac{{b}^{\mathrm{2}} +{ab}+{bc}}{\left({a}+{b}\right)\left({b}+{c}\right)}= \\ $$$$=\frac{{ac}}{\mathrm{2}}.\frac{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{ba}+\mathrm{2}{bc}}{\mathrm{2}\left({a}+{b}\right)\left({b}+{c}\right)}=\frac{{ac}}{\mathrm{2}}.\frac{\left({a}+{b}+{c}\right)^{\mathrm{2}} −\mathrm{2}{ac}}{\mathrm{2}{ab}+\mathrm{2}{ac}+\mathrm{2}{b}^{\mathrm{2}} +\mathrm{2}{bc}}= \\ $$$$={S}.\frac{\left(\mathrm{2}{p}\right)^{\mathrm{2}} −\mathrm{4}{S}}{\left(\mathrm{2}{p}\right)^{\mathrm{2}} }={S}.\frac{{p}^{\mathrm{2}} −{S}}{{p}^{\mathrm{2}} }={S}−\frac{{S}^{\mathrm{2}} }{{p}^{\mathrm{2}} }={S}−{r}^{\mathrm{2}} = \\ $$$$={r}.{p}−{r}^{\mathrm{2}} ={r}.\left({p}−{r}\right)={r}.{b}=\mathrm{2}{S}_{{AEA}'} .\:\:\blacksquare \\ $$$${note}:{in}\:{right}\:{angle}\:{triangle}:\boldsymbol{{b}}=\boldsymbol{{p}}−\boldsymbol{{r}} \\ $$$$\:{because}:\:\:{p}−{r}={p}−\frac{{S}}{{p}}=\frac{{p}^{\mathrm{2}} −{S}}{{p}}= \\ $$$$=\frac{\left({a}+{b}+{c}\right)^{\mathrm{2}} −\mathrm{2}{ac}}{\mathrm{4}{p}}=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{2}{ab}+\mathrm{2}{bc}}{\mathrm{4}{p}} \\ $$$$=\frac{\mathrm{2}{b}^{\mathrm{2}} +\mathrm{2}{ba}+\mathrm{2}{bc}}{\mathrm{4}{p}}=\frac{\mathrm{2}{b}\left({a}+{b}+{c}\right)}{\mathrm{4}{p}}=\frac{\mathrm{2}{b}.\mathrm{2}{p}}{\mathrm{4}{p}}=\boldsymbol{{b}}. \\ $$

Commented by behi83417@gmail.com last updated on 07/Jul/18

DC^2 =DB^2 +CB^2 =(((ac)/(a+b)))^2 +(((ac)/(c+b)))^2 = a^2 c^2 .(((b+c)^2 +(b+a)^2 )/((a+b)^2 (c+b)^2 ))=((4S^2 b(b+p))/(4p^4 ))= =(S^2 /p^2 ).b.((b+p)/p^2 )=b.r^2 .((2p−r)/p^2 )=b.(r^2 /p^2 )(2p−r) ⇒((DC)/(AA′))=(r^2 /p^2 )(2p−r). note: (b+c)^2 +(b+a)^2 =3b^2 +2bc+2ab= b(3b+a+c)=b(2b+2p)=2b(b+p) (a+b)(c+b)=ac+ab+bc+b^2 = =((a^2 +b^2 +c^2 +2ac+2bc+2ab)/2)=(((2p)^2 )/2)=2p^2

$${DC}^{\mathrm{2}} ={DB}^{\mathrm{2}} +{CB}^{\mathrm{2}} =\left(\frac{{ac}}{{a}+{b}}\right)^{\mathrm{2}} +\left(\frac{{ac}}{{c}+{b}}\right)^{\mathrm{2}} = \\ $$$${a}^{\mathrm{2}} {c}^{\mathrm{2}} .\frac{\left({b}+{c}\right)^{\mathrm{2}} +\left({b}+{a}\right)^{\mathrm{2}} }{\left({a}+{b}\right)^{\mathrm{2}} \left({c}+{b}\right)^{\mathrm{2}} }=\frac{\mathrm{4}{S}^{\mathrm{2}} {b}\left({b}+{p}\right)}{\mathrm{4}{p}^{\mathrm{4}} }= \\ $$$$=\frac{{S}^{\mathrm{2}} }{{p}^{\mathrm{2}} }.{b}.\frac{{b}+{p}}{{p}^{\mathrm{2}} }={b}.{r}^{\mathrm{2}} .\frac{\mathrm{2}{p}−{r}}{{p}^{\mathrm{2}} }={b}.\frac{{r}^{\mathrm{2}} }{{p}^{\mathrm{2}} }\left(\mathrm{2}{p}−{r}\right) \\ $$$$\Rightarrow\frac{{DC}}{{AA}'}=\frac{{r}^{\mathrm{2}} }{{p}^{\mathrm{2}} }\left(\mathrm{2}{p}−{r}\right). \\ $$$${note}: \\ $$$$\left({b}+{c}\right)^{\mathrm{2}} +\left({b}+{a}\right)^{\mathrm{2}} =\mathrm{3}{b}^{\mathrm{2}} +\mathrm{2}{bc}+\mathrm{2}{ab}= \\ $$$${b}\left(\mathrm{3}{b}+{a}+{c}\right)={b}\left(\mathrm{2}{b}+\mathrm{2}{p}\right)=\mathrm{2}{b}\left({b}+{p}\right) \\ $$$$\left({a}+{b}\right)\left({c}+{b}\right)={ac}+{ab}+{bc}+{b}^{\mathrm{2}} = \\ $$$$=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{2}{ac}+\mathrm{2}{bc}+\mathrm{2}{ab}}{\mathrm{2}}=\frac{\left(\mathrm{2}{p}\right)^{\mathrm{2}} }{\mathrm{2}}=\mathrm{2}{p}^{\mathrm{2}} \\ $$

Commented by behi83417@gmail.com last updated on 08/Jul/18

S_(ACE) =(1/2).r.A′C=(1/2).r.((ab)/(b+c)) S_(ADE) =(1/2).r.AD=(1/2).r.((c.b)/(a+b)) S_(DEC) =2S_(AEA′) −S_(AEA′) −((b.r)/2)((a/(b+c))+(c/(a+b)))= =((b.r)/2)(1−(a/(b+c))−(c/(a+b)))=((br(ab+ac+bc+b^2 −a^2 −ab−c^2 −cb))/(2(b+c)(b+a)))= =((br.ac)/(4p^2 ))=((br.2S)/(4p^2 ))=(b/(2p)) ⇒(S_(AEA′) /S_(DRC) )=(((br)/2)/(b/(2p)))=r.p (????????????→∞)

$${S}_{{ACE}} =\frac{\mathrm{1}}{\mathrm{2}}.{r}.{A}'{C}=\frac{\mathrm{1}}{\mathrm{2}}.{r}.\frac{{ab}}{{b}+{c}} \\ $$$${S}_{{ADE}} =\frac{\mathrm{1}}{\mathrm{2}}.{r}.{AD}=\frac{\mathrm{1}}{\mathrm{2}}.{r}.\frac{{c}.{b}}{{a}+{b}} \\ $$$${S}_{{DEC}} =\mathrm{2}{S}_{{AEA}'} −{S}_{{AEA}'} −\frac{{b}.{r}}{\mathrm{2}}\left(\frac{{a}}{{b}+{c}}+\frac{{c}}{{a}+{b}}\right)= \\ $$$$=\frac{{b}.{r}}{\mathrm{2}}\left(\mathrm{1}−\frac{{a}}{{b}+{c}}−\frac{{c}}{{a}+{b}}\right)=\frac{{br}\left({ab}+{ac}+{bc}+{b}^{\mathrm{2}} −{a}^{\mathrm{2}} −{ab}−{c}^{\mathrm{2}} −{cb}\right)}{\mathrm{2}\left({b}+{c}\right)\left({b}+{a}\right)}= \\ $$$$=\frac{{br}.{ac}}{\mathrm{4}{p}^{\mathrm{2}} }=\frac{{br}.\mathrm{2}{S}}{\mathrm{4}{p}^{\mathrm{2}} }=\frac{{b}}{\mathrm{2}{p}} \\ $$$$\Rightarrow\frac{{S}_{{AEA}'} }{{S}_{{DRC}} }=\frac{\frac{{br}}{\mathrm{2}}}{\frac{{b}}{\mathrm{2}{p}}}={r}.{p}\:\:\:\left(????????????\rightarrow\infty\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com