Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 39699 by maxmathsup by imad last updated on 09/Jul/18

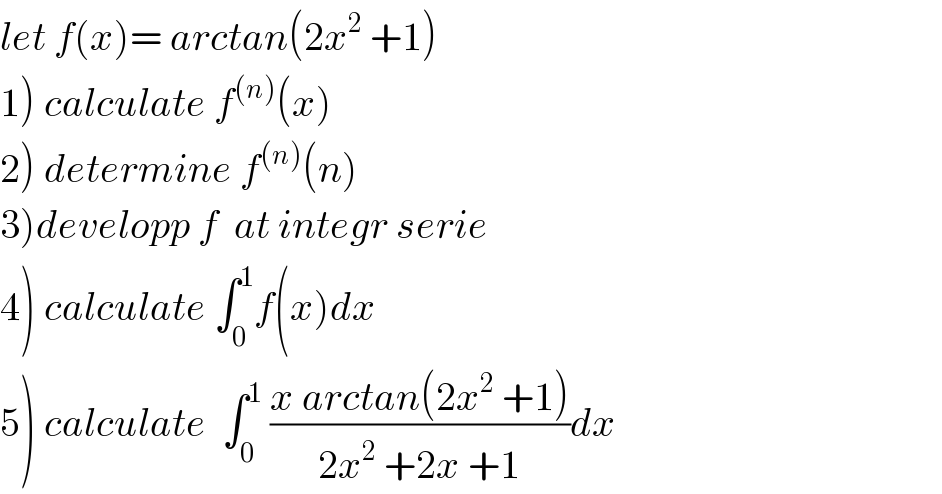
let f(x)= arctan(2x^2 +1) 1) calculate f^((n)) (x) 2) determine f^((n)) (n) 3)developp f at integr serie 4) calculate ∫_0 ^1 f(x)dx 5) calculate ∫_0 ^1 ((x arctan(2x^2 +1))/(2x^2 +2x +1))dx

$${let}\:{f}\left({x}\right)=\:{arctan}\left(\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}\right) \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{f}^{\left({n}\right)} \left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{determine}\:{f}^{\left({n}\right)} \left({n}\right) \\ $$$$\left.\mathrm{3}\right){developp}\:{f}\:\:{at}\:{integr}\:{serie} \\ $$$$\left.\mathrm{4}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx} \\ $$$$\left.\mathrm{5}\right)\:{calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}\:{arctan}\left(\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}\right)}{\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{2}{x}\:+\mathrm{1}}{dx} \\ $$

Commented by math khazana by abdo last updated on 10/Jul/18

2) determine f^((n)) (0)

$$\left.\mathrm{2}\right)\:{determine}\:{f}^{\left({n}\right)} \left(\mathrm{0}\right) \\ $$

Commented by maxmathsup by imad last updated on 13/Jul/18

4) let integrate by parts u^′ =1 and v =arctan(2x^2 +1) ∫_0 ^1 f(x)dx = [x arctan(2x^2 +1)]_0 ^1 −∫_0 ^1 x ((4x)/(1+(2x^2 +1)^2 ))dx =arctan(3)−4 ∫_0 ^1 (x^2 /(1+(2x^2 +1)^2 ))dx changement x =(1/(√2)) tanθ give ∫_0 ^1 (x^2 /(1+(2x^2 +1)^2 ))dx = ∫_0 ^(arctan((√2))) (1/2) ((tan^2 θ)/(1+(1+tan^2 θ)^2 )) (1/(√2))(1+tan^2 θ)dθ = (1/(2(√2))) ∫_0 ^(arctan((√2))) ((tan^2 θ(1+tan^2 θ))/(1+(1+tan^2 θ)^2 ))dθ =(1/(2(√2))) ∫_0 ^(arctan((√2))) ((((1/(cos^2 θ))−1)((1/(cos^2 θ))))/(1+ (1/(cos^4 θ))))dθ = (1/(2(√2))) ∫_0 ^(arctan((√2))) ((1−cos^2 θ)/(1+cos^4 θ)) dθ = (1/(2(√2))) ∫_0 ^(arctan((√2))) ((1−((1+cos(2θ))/2))/(1+(((1+cos(2θ))/2))^2 ))dθ = (1/(2(√2))) ∫_0 ^(arctan((√2))) ((1−cos(2θ))/(4+(1+cos(2θ))^2 )) 2dθ = (1/(√2)) ∫_0 ^(arctan((√2))) ((1−cos(2θ))/(4 +1 +2cos(2θ) +((1+cos(4θ))/4))) dθ =(4/(√2)) ∫_0 ^(arctan((√2))) ((1−cos(2θ))/(21 +8cos(2θ) +cos(4θ)))dθ ...be continued...

$$\left.\mathrm{4}\right)\:{let}\:{integrate}\:{by}\:{parts}\:{u}^{'} =\mathrm{1}\:{and}\:{v}\:={arctan}\left(\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}\:=\:\left[{x}\:{arctan}\left(\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}\:\:\frac{\mathrm{4}{x}}{\mathrm{1}+\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$={arctan}\left(\mathrm{3}\right)−\mathrm{4}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{x}^{\mathrm{2}} }{\mathrm{1}+\left(\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }{dx}\:\:{changement}\:{x}\:=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:{tan}\theta\:\:{give} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{x}^{\mathrm{2}} }{\mathrm{1}+\left(\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }{dx}\:=\:\int_{\mathrm{0}} ^{{arctan}\left(\sqrt{\mathrm{2}}\right)} \:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\:\frac{{tan}^{\mathrm{2}} \theta}{\mathrm{1}+\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)^{\mathrm{2}} }\:\:\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){d}\theta \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\int_{\mathrm{0}} ^{{arctan}\left(\sqrt{\mathrm{2}}\right)} \:\:\frac{{tan}^{\mathrm{2}} \theta\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)}{\mathrm{1}+\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)^{\mathrm{2}} }{d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\int_{\mathrm{0}} ^{{arctan}\left(\sqrt{\mathrm{2}}\right)} \:\frac{\left(\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \theta}−\mathrm{1}\right)\left(\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \theta}\right)}{\mathrm{1}+\:\frac{\mathrm{1}}{{cos}^{\mathrm{4}} \theta}}{d}\theta \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\int_{\mathrm{0}} ^{{arctan}\left(\sqrt{\mathrm{2}}\right)} \:\:\frac{\mathrm{1}−{cos}^{\mathrm{2}} \theta}{\mathrm{1}+{cos}^{\mathrm{4}} \theta}\:{d}\theta\:\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\int_{\mathrm{0}} ^{{arctan}\left(\sqrt{\mathrm{2}}\right)} \:\:\:\:\frac{\mathrm{1}−\frac{\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}}}{\mathrm{1}+\left(\frac{\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}}\right)^{\mathrm{2}} }{d}\theta \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\int_{\mathrm{0}} ^{{arctan}\left(\sqrt{\mathrm{2}}\right)} \:\:\:\:\frac{\mathrm{1}−{cos}\left(\mathrm{2}\theta\right)}{\mathrm{4}+\left(\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)\right)^{\mathrm{2}} }\:\mathrm{2}{d}\theta \\ $$$$=\:\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:\int_{\mathrm{0}} ^{{arctan}\left(\sqrt{\mathrm{2}}\right)} \:\:\:\frac{\mathrm{1}−{cos}\left(\mathrm{2}\theta\right)}{\mathrm{4}\:+\mathrm{1}\:+\mathrm{2}{cos}\left(\mathrm{2}\theta\right)\:\:+\frac{\mathrm{1}+{cos}\left(\mathrm{4}\theta\right)}{\mathrm{4}}}\:{d}\theta \\ $$$$=\frac{\mathrm{4}}{\sqrt{\mathrm{2}}}\:\:\int_{\mathrm{0}} ^{{arctan}\left(\sqrt{\mathrm{2}}\right)} \:\:\:\:\:\:\frac{\mathrm{1}−{cos}\left(\mathrm{2}\theta\right)}{\mathrm{21}\:+\mathrm{8}{cos}\left(\mathrm{2}\theta\right)\:+{cos}\left(\mathrm{4}\theta\right)}{d}\theta\:\:...{be}\:{continued}... \\ $$

Commented by maxmathsup by imad last updated on 13/Jul/18

1) we have f^′ (x)= ((4x)/(1+(2x^2 +1)^2 )) ⇒f^((n)) (x)=4{ (x/(1+(2x^2 +1)^2 ))}^((n−1)) let w(x)= (x/(1+(2x^2 +1)^2 )) let decompose w(x) w(x) = (x/((2x^2 +1)^2 −i^2 )) = (x/((2x^2 +1−i)(2x^2 +1+i))) = (x/(4( x^2 +((1−i)/2))(x^2 +((1+i)/2)))) = (x/(4( x^2 +(1/(√2))e^(−((iπ)/4)) )(x^2 +(1/(√2))e^((iπ)/4) ))) = (x/(4(x−(i/((√(√2)) ))e^(−((iπ)/8)) )(x+ (i/(√(√2))) e^(−((iπ)/8)) )(x−(i/(√(√2))) e^((iπ)/8) )(x+(1/(√(√2))) e^((iπ)/8) ))) let z_0 =(i/(√(√2))) e^((iπ)/8) , z_1 =−(i/(√(√2))) e^((iπ)/8) , z_2 = (i/(√(√2))) e^(−((iπ)/8)) , z_3 = −(i/(√(√2))) e^(−((iπ)/8)) ⇒ f^′ (x) =4w(x) = (a/(x−z_0 )) +(b/(x−z_1 )) +(c/(x−z_2 )) +(d/(x−z_3 )) =(x/((x−z_0 )(x−z_1 )(x−z_2 )(x−z_3 ))) we have a = (z_0 /((z_0 −z_1 )(z_0 ^2 + (1/(√2))e^(−((iπ)/4)) ))) b = (z_1 /((z_1 −z_0 )(z_1 ^2 +(1/(√2))e^(−((iπ)/4)) ))) c = (z_2 /((z_2 −z_3 )(z_2 ^2 +(1/(√2))e^((iπ)/4) ))) d = (z_3 /((z_3 −z_2 )(z_3 ^2 +(1/(√2))e^((iπ)/4) ))) and f^((n)) (x) = a (((−1)^(n−1) (n−1)!)/((x−z_0 )^n )) +b (((−1)^(n−1) (n−1)!)/((x−z_1 )^n )) + c (((−1)^(n−1) (n−1)!)/((x−z_2 )^n )) +d (((−1)^(n−1) (n−1)!)/((x−z_3 )^n )) 2) f^((n)) (0) = (−1)^(n−1) (n−1)!{ (a/((−z_0 )^n )) + (b/((−z_1 )^n )) + (c/((−z_2 )^n )) +(d/((−z_3 )^n ))} =−(n−1)!{ (a/z_0 ^n ) +(b/z_1 ^n ) + (c/z_2 ^n ) +(d/z_3 ^n )} 3) we have f(x) =Σ_(n=0) ^∞ ((f^((n)) (0))/(n!)) x^n =(π/4) −Σ_(n=1) ^∞ (1/n){ (a/z_0 ^n ) +(b/z_1 ^n ) + (c/z_2 ^n ) +(d/z_3 ^n )}x^n

$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}^{'} \left({x}\right)=\:\frac{\mathrm{4}{x}}{\mathrm{1}+\left(\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow{f}^{\left({n}\right)} \left({x}\right)=\mathrm{4}\left\{\:\frac{{x}}{\mathrm{1}+\left(\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\right\}^{\left({n}−\mathrm{1}\right)} \\ $$$${let}\:{w}\left({x}\right)=\:\frac{{x}}{\mathrm{1}+\left(\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:{let}\:\:{decompose}\:{w}\left({x}\right) \\ $$$${w}\left({x}\right)\:=\:\:\frac{{x}}{\left(\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} \:−{i}^{\mathrm{2}} }\:=\:\frac{{x}}{\left(\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}−{i}\right)\left(\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}+{i}\right)} \\ $$$$=\:\frac{{x}}{\mathrm{4}\left(\:{x}^{\mathrm{2}} \:+\frac{\mathrm{1}−{i}}{\mathrm{2}}\right)\left({x}^{\mathrm{2}} \:+\frac{\mathrm{1}+{i}}{\mathrm{2}}\right)}\:\:=\:\frac{{x}}{\mathrm{4}\left(\:{x}^{\mathrm{2}} \:+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\left({x}^{\mathrm{2}} \:+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)} \\ $$$$=\:\frac{{x}}{\mathrm{4}\left({x}−\frac{{i}}{\sqrt{\sqrt{\mathrm{2}}}\:}{e}^{−\frac{{i}\pi}{\mathrm{8}}} \right)\left({x}+\:\frac{{i}}{\sqrt{\sqrt{\mathrm{2}}}}\:{e}^{−\frac{{i}\pi}{\mathrm{8}}} \right)\left({x}−\frac{{i}}{\sqrt{\sqrt{\mathrm{2}}}}\:{e}^{\frac{{i}\pi}{\mathrm{8}}} \right)\left({x}+\frac{\mathrm{1}}{\sqrt{\sqrt{\mathrm{2}}}}\:{e}^{\frac{{i}\pi}{\mathrm{8}}} \right)}\:\:{let} \\ $$$${z}_{\mathrm{0}} =\frac{{i}}{\sqrt{\sqrt{\mathrm{2}}}}\:{e}^{\frac{{i}\pi}{\mathrm{8}}} \:\:,\:\:{z}_{\mathrm{1}} \:=−\frac{{i}}{\sqrt{\sqrt{\mathrm{2}}}}\:{e}^{\frac{{i}\pi}{\mathrm{8}}} \:\:\:,\:{z}_{\mathrm{2}} =\:\frac{{i}}{\sqrt{\sqrt{\mathrm{2}}}}\:{e}^{−\frac{{i}\pi}{\mathrm{8}}} \:\:,\:\:{z}_{\mathrm{3}} \:=\:−\frac{{i}}{\sqrt{\sqrt{\mathrm{2}}}}\:{e}^{−\frac{{i}\pi}{\mathrm{8}}} \:\Rightarrow \\ $$$${f}^{'} \left({x}\right)\:=\mathrm{4}{w}\left({x}\right)\:=\:\:\frac{{a}}{{x}−{z}_{\mathrm{0}} }\:+\frac{{b}}{{x}−{z}_{\mathrm{1}} }\:+\frac{{c}}{{x}−{z}_{\mathrm{2}} }\:+\frac{{d}}{{x}−{z}_{\mathrm{3}} }\:=\frac{{x}}{\left({x}−{z}_{\mathrm{0}} \right)\left({x}−{z}_{\mathrm{1}} \right)\left({x}−{z}_{\mathrm{2}} \right)\left({x}−{z}_{\mathrm{3}} \right)} \\ $$$${we}\:{have}\:\:\:{a}\:=\:\:\frac{{z}_{\mathrm{0}} }{\left({z}_{\mathrm{0}} −{z}_{\mathrm{1}} \right)\left({z}_{\mathrm{0}} ^{\mathrm{2}} \:+\:\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)} \\ $$$${b}\:=\:\frac{{z}_{\mathrm{1}} }{\left({z}_{\mathrm{1}} −{z}_{\mathrm{0}} \right)\left({z}_{\mathrm{1}} ^{\mathrm{2}} \:+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)} \\ $$$${c}\:=\:\:\frac{{z}_{\mathrm{2}} }{\left({z}_{\mathrm{2}} −{z}_{\mathrm{3}} \right)\left({z}_{\mathrm{2}} ^{\mathrm{2}} \:+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)} \\ $$$${d}\:=\:\:\frac{{z}_{\mathrm{3}} }{\left({z}_{\mathrm{3}} −{z}_{\mathrm{2}} \right)\left({z}_{\mathrm{3}} ^{\mathrm{2}} \:\:+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)}\:\:{and}\:\: \\ $$$${f}^{\left({n}\right)} \left({x}\right)\:=\:{a}\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\left({x}−{z}_{\mathrm{0}} \right)^{{n}} }\:\:+{b}\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\left({x}−{z}_{\mathrm{1}} \right)^{{n}} }\:+\:{c}\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\left({x}−{z}_{\mathrm{2}} \right)^{{n}} } \\ $$$$+{d}\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\left({x}−{z}_{\mathrm{3}} \right)^{{n}} } \\ $$$$\left.\mathrm{2}\right)\:{f}^{\left({n}\right)} \left(\mathrm{0}\right)\:=\:\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!\left\{\:\:\:\:\frac{{a}}{\left(−{z}_{\mathrm{0}} \right)^{{n}} }\:+\:\frac{{b}}{\left(−{z}_{\mathrm{1}} \right)^{{n}} }\:+\:\frac{{c}}{\left(−{z}_{\mathrm{2}} \right)^{{n}} }\:+\frac{{d}}{\left(−{z}_{\mathrm{3}} \right)^{{n}} }\right\} \\ $$$$=−\left({n}−\mathrm{1}\right)!\left\{\:\:\:\frac{{a}}{{z}_{\mathrm{0}} ^{{n}} }\:\:+\frac{{b}}{{z}_{\mathrm{1}} ^{{n}} }\:+\:\frac{{c}}{{z}_{\mathrm{2}} ^{{n}} }\:+\frac{{d}}{{z}_{\mathrm{3}} ^{{n}} }\right\} \\ $$$$\left.\mathrm{3}\right)\:{we}\:{have}\:{f}\left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{{f}^{\left({n}\right)} \left(\mathrm{0}\right)}{{n}!}\:{x}^{{n}} \\ $$$$=\frac{\pi}{\mathrm{4}}\:−\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\mathrm{1}}{{n}}\left\{\:\frac{{a}}{{z}_{\mathrm{0}} ^{{n}} }\:+\frac{{b}}{{z}_{\mathrm{1}} ^{{n}} }\:+\:\frac{{c}}{{z}_{\mathrm{2}} ^{{n}} }\:+\frac{{d}}{{z}_{\mathrm{3}} ^{{n}} }\right\}{x}^{{n}} \\ $$

Commented by maxmathsup by imad last updated on 13/Jul/18

5) we have f^′ (x)= ((4x)/(1+(2x^2 +1)^2 )) = ((4x)/(1+4x^4 +4x^2 +1)) = ((4x)/(4x^4 +4x^2 +2)) = ((2x)/(2x^4 +2x^2 +1)) ⇒(x/(2x^4 +2x^2 +1)) =(1/2)f^′ (x) ⇒let integrate by parts ∫_0 ^1 ((x arctan(2x^2 +1))/(2x^4 +2x^2 +1)) dx =(1/2) ∫_0 ^1 f.f^′ dx=[(1/4) f^2 (x)]_0 ^1 =(1/4){ f^2 (1) −f^((2)) (0)} =(1/4){ arctan^2 (3) −(π^2 /(16))} .

$$\left.\mathrm{5}\right)\:{we}\:{have}\:{f}^{'} \left({x}\right)=\:\frac{\mathrm{4}{x}}{\mathrm{1}+\left(\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:=\:\frac{\mathrm{4}{x}}{\mathrm{1}+\mathrm{4}{x}^{\mathrm{4}} \:+\mathrm{4}{x}^{\mathrm{2}} \:+\mathrm{1}}\:=\:\frac{\mathrm{4}{x}}{\mathrm{4}{x}^{\mathrm{4}} \:+\mathrm{4}{x}^{\mathrm{2}} \:+\mathrm{2}} \\ $$$$=\:\frac{\mathrm{2}{x}}{\mathrm{2}{x}^{\mathrm{4}} \:+\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\frac{{x}}{\mathrm{2}{x}^{\mathrm{4}} \:+\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{2}}{f}^{'} \left({x}\right)\:\Rightarrow{let}\:{integrate}\:{by}\:{parts} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{x}\:{arctan}\left(\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}\right)}{\mathrm{2}{x}^{\mathrm{4}} \:+\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}}\:{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{f}.{f}^{'} {dx}=\left[\frac{\mathrm{1}}{\mathrm{4}}\:{f}^{\mathrm{2}} \left({x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left\{\:{f}^{\mathrm{2}} \left(\mathrm{1}\right)\:−{f}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)\right\}\:=\frac{\mathrm{1}}{\mathrm{4}}\left\{\:{arctan}^{\mathrm{2}} \left(\mathrm{3}\right)\:−\frac{\pi^{\mathrm{2}} }{\mathrm{16}}\right\}\:. \\ $$$$ \\ $$

Commented by maxmathsup by imad last updated on 13/Jul/18

5) the Q is[find ∫_0 ^1 ((x arctan(2x^2 +1))/(2x^4 +2x^2 +1)) dx .

$$\left.\mathrm{5}\right)\:{the}\:{Q}\:{is}\left[{find}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{x}\:{arctan}\left(\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}\right)}{\mathrm{2}{x}^{\mathrm{4}} \:+\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}}\:{dx}\:.\right. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com