if f(x) = 3x^3 + px^2 + 4x − 8 and (x − 1) is a factor of f(x). a) find the value of p. with these value of p b) solve the equation f(x) = 0. if α and β are roots of f(x), c) find α + β and αβ d) Evaluate α^2 + β^2 hence α − β


Question and Answers Forum

All Questions Topic List
Others Questions
Previous in All Question Next in All Question
Previous in Others Next in Others
Question Number 39827 by Rio Mike last updated on 11/Jul/18

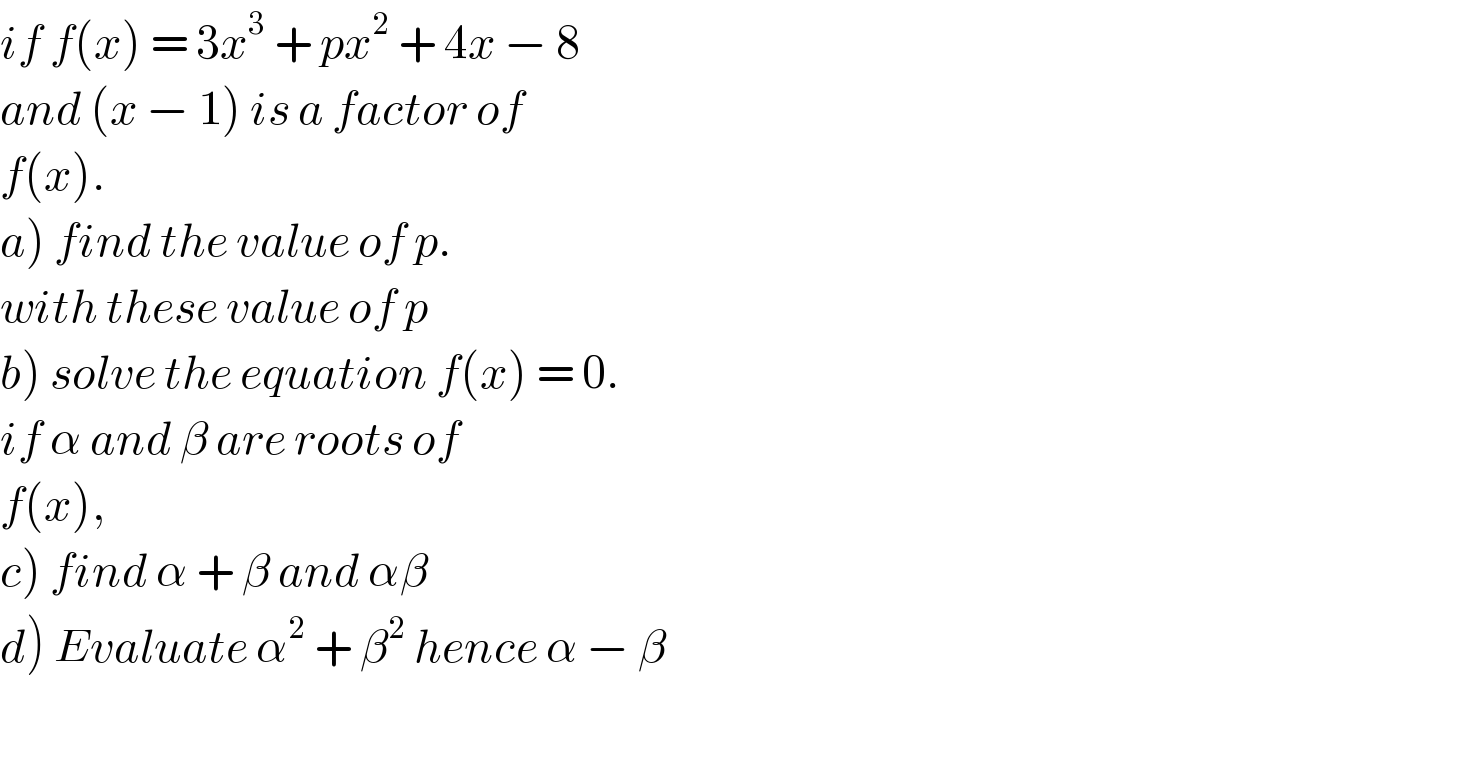
$i f f (x) = 3 x^{3} + {p x}^{2} + 4 x - 8$ $a n d (x - 1) i s a f a c t o r o f$ $f (x) .$ $a) f i n d t h e v a l u e o f p .$ $w i t h t h e s e v a l u e o f p$ $b) s o l v e t h e e q u a t i o n f (x) = 0 .$ $i f α a n d β a r e r o o t s o f$ $f (x),$ $c) f i n d α + β a n d α β$ $d) E v a l u a t e α^{2} + β^{2} h e n c e α - β$
	Answered by MJS last updated on 11/Jul/18

	$3 (x - 1) (x - α) (x - β) = 3 x^{3} + {p x}^{2} + 4 x - 8$ $3 x^{3} - 3 (α + β + 1) x^{2} + 3 (α + α β + β) x - 3 α β =$ $= 3 x^{3} + {p x}^{2} + 4 x - 8$ $\Rightarrow$ $p = - 3 (α + β + 1)$ $3 (α + α β + β) = 4$ $3 α β = 8 \Rightarrow α = \frac{8}{3 β}$ $3 (\frac{8}{3 β} + \frac{8}{3 β} β + β) = 4 \Rightarrow β^{2} + \frac{4}{3} β + \frac{8}{3} = 0 \Rightarrow$ $\Rightarrow β = - \frac{2}{3} \pm \frac{2 \sqrt{5}}{3} i$ $\Rightarrow α = - \frac{2}{3} \mp \frac{2 \sqrt{5}}{3} i$ $\Rightarrow p = 1$ $α + β = - \frac{4}{3}$ $α β = \frac{8}{3}$ $α^{2} + β^{2} = - \frac{32}{9}$ $α - β = \pm \frac{4 \sqrt{5}}{3} i$
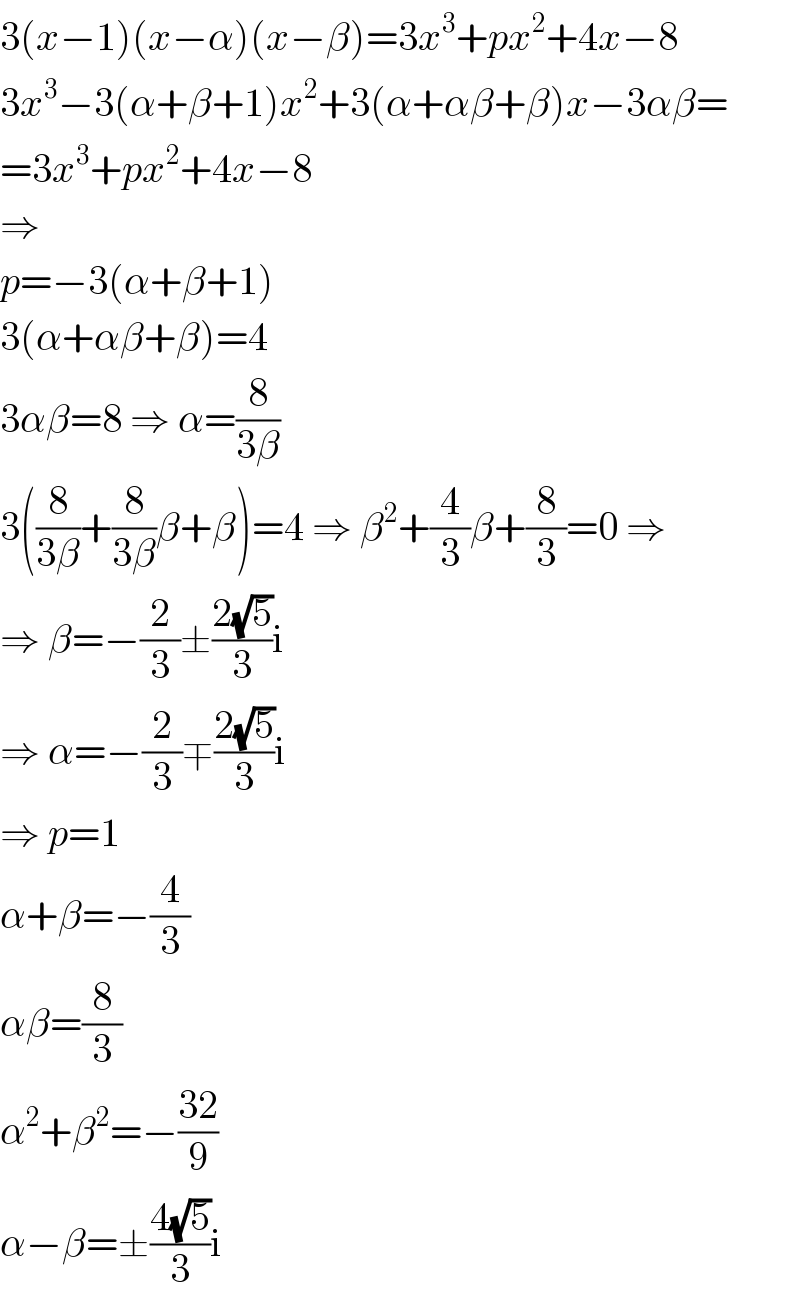
	Commented by Rio Mike last updated on 12/Jul/18

	$t h e c u b i c e x p r e s s i o n i s o f$ $t h e f o r m$ $y = {a x}^{3} + {b x}^{2} + c x + d$ $s o w h a t i s α + \overset{}{β} = ?$ $a n d α β = ?$
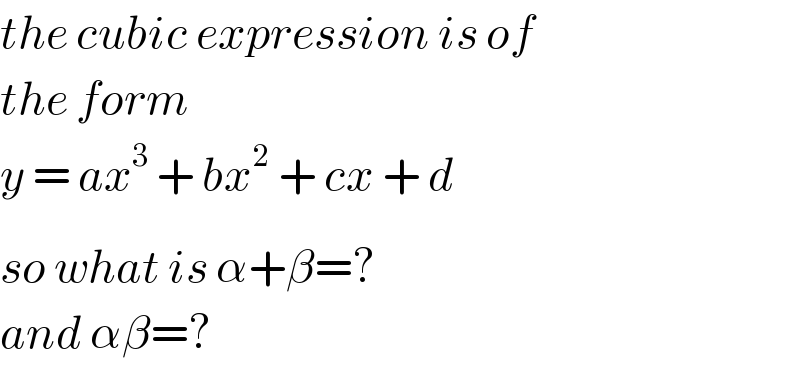
	Commented by MJS last updated on 12/Jul/18

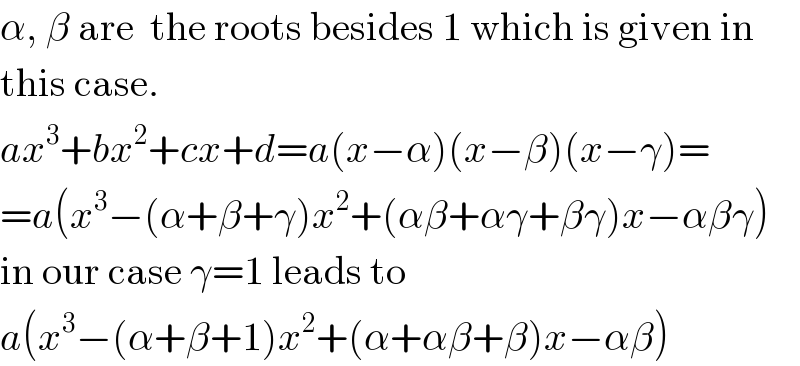
	$α, β are the roots besides 1 which is given in$ $this case .$ ${a x}^{3} + {b x}^{2} + c x + d = a (x - α) (x - β) (x - γ) =$ $= a (x^{3} - (α + β + γ) x^{2} + (α β + α γ + β γ) x - α β γ)$ $in our case γ = 1 leads to$ $a (x^{3} - (α + β + 1) x^{2} + (α + α β + β) x - α β)$
	Answered by Rasheed.Sindhi last updated on 13/Jul/18

	$AnOther approach$ $If f (x) is divided by x - 1 then the$ $quotient Q (x) and remainder R can$ $be determined by synthetic division :$ $(\begin{matrix} 1) 3 & p & 4 & - 8 \\ 3 & p + 3 & p + 7 \\ 3 & p + 3 & p + 7 & ∣ \overset{―}{p - 1} \end{matrix})$ $∵ x - 1 is factor of f (x)$ $∴ R = p - 1 = 0 \Rightarrow p = 1 (a)$ $Q (x) = {3 x}^{2} + (p + 3) x + (p + 7)$ $= {3 x}^{2} + (1 + 3) x + (1 + 7)$ $= {3 x}^{2} + 4 x + 8$ $f (x) = (x - 1) . Q (x) + R$ $[Relation between divedend, divisor & remainder]$ $= (x - 1) . Q (x) + 0$ $= (x - 1) ({3 x}^{2} + 4 x + 8)$ $(b) f (x) = 0 \Rightarrow x - 1 = 0 ∣ {3 x}^{2} + 4 x + 8 = 0$ $x = 1 ∣ x = \frac{- 4 \pm \sqrt{16 - 96}}{6}$ $∣ x = \frac{- 2 \pm 2 i \sqrt{5}}{3}$ $Let α & β are the roots of {3 x}^{2} + 4 x + 8 = 0$ $α + β = - \frac{4}{3} & α β = \frac{8}{3}$ $α - β = \frac{- 2 + 2 i \sqrt{5}}{3} - \frac{- 2 - 2 i \sqrt{5}}{3}$ $= \frac{4 \sqrt{5}}{3} i$ $α^{2} + β^{2} = {(α + β)}^{2} - 2 α β = {(- \frac{4}{3})}^{2} - 2 (\frac{8}{3})$ $= \frac{16}{9} - \frac{16}{3} = \frac{16 - 48}{9} = - \frac{32}{9}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum