
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 39839 by math khazana by abdo last updated on 12/Jul/18
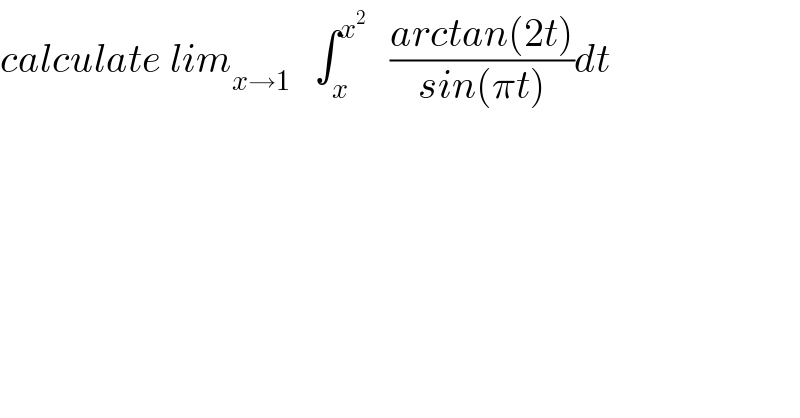
Commented by math khazana by abdo last updated on 30/Jul/18
![let f(x)= ∫_x ^x^2 ((arctan(2t))/(sin(πt))) dt changement t=u+1 give f(x)= ∫_(x−1) ^(x^2 −1) ((arctan(2u+2))/(sin(πu +π)))du =− ∫_(x−1) ^(x^2 −1) ((arctan(2u+2))/(sin(πu))) du but ∃c ∈]x−1,x^2 −1[/ f(x)=−arctan(2c+2) ∫_(x−1) ^(x^2 −1) (du/(sin(πu))) we have ∫_(x−1) ^(x^2 −1) (du/(sin(πu))) =_(πu =t) ∫_(π(x−1)) ^(π(x^2 −1)) (dt/(πsint)) =_(tan((t/2)) =α) (1/π) ∫_(tan((π/2)(x−1))) ^(tan((π/2)(x^2 −1))) (1/((2α)/(1+α^2 ))) ((2dα)/(1+α^2 )) =(1/π)[ln∣α∣]_(tan((π/2)(x−1))) ^(tan((π/2)(x^2 −1))) =(1/π)ln∣((tan((π/2)(x^2 −1)))/(tan((π/2)(x−1))))∣ for x∈v(1) tan((π/2)(x^2 −1))∼(π/2)(x^2 −1) and tan((π/2)(x−1))∼ (π/2)(x−1) ⇒∣((tan(...))/(tan(..)))∣∼∣x+1∣⇒ lim_(x→1) ∫_(x−1) ^(x^2 −1) (du/(sin(πu))) =((ln(2))/π) ⇒ lim_(x→1) f(x)=−arctan(2)((ln(2))/π) .](Q40947.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 39839 by math khazana by abdo last updated on 12/Jul/18 | ||
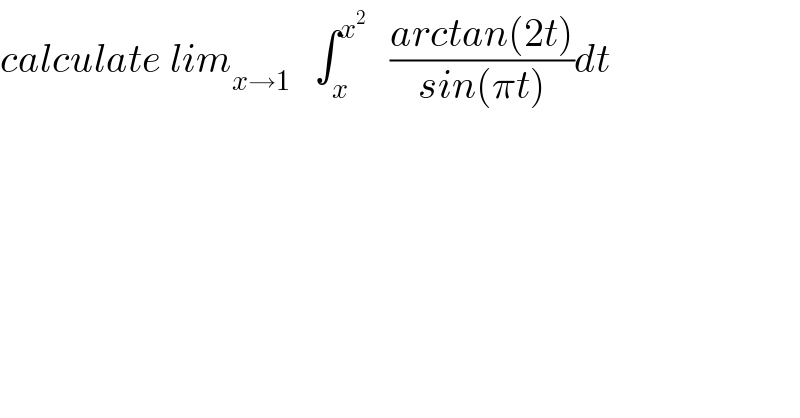 | ||
Commented by math khazana by abdo last updated on 30/Jul/18 | ||
![let f(x)= ∫_x ^x^2 ((arctan(2t))/(sin(πt))) dt changement t=u+1 give f(x)= ∫_(x−1) ^(x^2 −1) ((arctan(2u+2))/(sin(πu +π)))du =− ∫_(x−1) ^(x^2 −1) ((arctan(2u+2))/(sin(πu))) du but ∃c ∈]x−1,x^2 −1[/ f(x)=−arctan(2c+2) ∫_(x−1) ^(x^2 −1) (du/(sin(πu))) we have ∫_(x−1) ^(x^2 −1) (du/(sin(πu))) =_(πu =t) ∫_(π(x−1)) ^(π(x^2 −1)) (dt/(πsint)) =_(tan((t/2)) =α) (1/π) ∫_(tan((π/2)(x−1))) ^(tan((π/2)(x^2 −1))) (1/((2α)/(1+α^2 ))) ((2dα)/(1+α^2 )) =(1/π)[ln∣α∣]_(tan((π/2)(x−1))) ^(tan((π/2)(x^2 −1))) =(1/π)ln∣((tan((π/2)(x^2 −1)))/(tan((π/2)(x−1))))∣ for x∈v(1) tan((π/2)(x^2 −1))∼(π/2)(x^2 −1) and tan((π/2)(x−1))∼ (π/2)(x−1) ⇒∣((tan(...))/(tan(..)))∣∼∣x+1∣⇒ lim_(x→1) ∫_(x−1) ^(x^2 −1) (du/(sin(πu))) =((ln(2))/π) ⇒ lim_(x→1) f(x)=−arctan(2)((ln(2))/π) .](Q40947.png) | ||