Question Number 39860 by ajfour last updated on 12/Jul/18
Commented by ajfour last updated on 12/Jul/18
$${OA}\:=\:{BP}\:\:\:,\:{OT}\:=\mathrm{1},\:\:\:\&\: \\ $$$$\angle{OTB}\:=\:\angle{BTP}\:\:\:\left({given}\:{conditions}\right). \\ $$
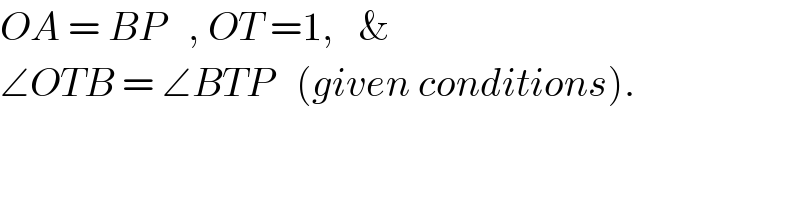
Answered by ajfour last updated on 13/Jul/18
![((xx_T )/a^2 )+((yy_T )/b^2 )=1 (eq. of tangent at T) (0, b+a) lies on this tangent ⇒ y_T = (b^2 /(a+b)) .....(i) And since (x_T ^2 /a^2 )+(y_T ^2 /b^2 )=1 , hence x_T ^2 = a^2 −((a^2 b^2 )/((a+b)^2 )) ...(ii) As OT=1 so x_T ^2 +y_T ^2 = 1 ⇒ a^2 −((a^2 b^2 )/((a+b)^2 ))+(b^4 /((a+b)^2 )) =1 ...(iii) (a^2 −1)=((b^2 (a^2 −b^2 ))/((a+b)^2 )) one solution of this eq. is a=b=1 , otherwise a^2 −1 = ((b^2 (a−b))/(a+b)) if a=br then b^2 r^2 −1=b^2 (((r−1)/(r+1))) b^2 (r^2 −((r−1)/(r+1)))=1 ...(iv) And as ( ((PT)/(OT)) = ((BP)/(OB)) )^2 ⇒ ((x_T ^2 +[(a+b)−y_T ]^2 )/1) = (a^2 /b^2 ) ⇒ a^2 −((a^2 b^2 )/((a+b)^2 ))+(a+b)^2 +y_T ^2 −2(a+b)y_T = (a^2 /b^2 ) ⇒ a^2 −((a^2 b^2 )/((a+b)^2 ))+(a+b)^2 +(b^4 /((a+b)^2 )) −2b^2 = (a^2 /b^2 ) ...(v) using (iii) in above eq. (v) 1+(a+b)^2 −2b^2 = (a^2 /b^2 ) again with a=br 1+b^2 (r+1)^2 −2b^2 =r^2 ⇒ b^2 (r^2 +2r−1)=r^2 −1 ...(vi) comparing (iv) and (vi) ⇒ ((r^2 +2r−1)/(r^2 −((r−1)/(r+1)))) = ((r^2 −1)/1) ⇒ ((2r)/(r^2 −1−((r−1)/(r+1)))) = r^2 −1 2r(r+1)=(r^2 −1)[(r^2 −1)(r+1)−(r−1)] ⇒ 2r=(r−1)^2 [(r+1)^2 −1] ⇒ 2r = (r^2 −1)^2 −(r−1)^2 or r^4 −3r^2 =0 ⇒ r= (√3) (valid answer) Now from (vi) we have b^2 = ((r^2 −1)/(r^2 +2r−1)) = (2/(2+2(√3))) = (1/(1+(√3))) = (((√3)−1)/2) While a^2 = b^2 r^2 = ((3((√3)−1))/2) Ellipse eq. is thus ((2x^2 )/(3((√3)−1)))+((2y^2 )/((√3)−1)) =1 or _(______________________) 2x^2 +6y^2 = 3(√3)−3 ^( _______________________ .)](Q39890.png)
$$\frac{{xx}_{{T}} }{{a}^{\mathrm{2}} }+\frac{{yy}_{{T}} }{{b}^{\mathrm{2}} }=\mathrm{1}\:\:\:\left({eq}.\:{of}\:{tangent}\:{at}\:{T}\right) \\ $$$$\left(\mathrm{0},\:{b}+{a}\right)\:{lies}\:{on}\:{this}\:{tangent} \\ $$$$\Rightarrow\:\:\boldsymbol{{y}}_{\boldsymbol{{T}}} =\:\frac{\boldsymbol{{b}}^{\mathrm{2}} }{\boldsymbol{{a}}+\boldsymbol{{b}}}\:\:\:\:\:\:\:\:.....\left(\boldsymbol{{i}}\right) \\ $$$${And}\:{since}\:\frac{{x}_{{T}} ^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}_{{T}} ^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}\:\:\:,\:{hence} \\ $$$$\:\:\:\:\:\:\:\boldsymbol{{x}}_{\boldsymbol{{T}}} ^{\mathrm{2}} \:=\:\boldsymbol{{a}}^{\mathrm{2}} −\frac{\boldsymbol{{a}}^{\mathrm{2}} \boldsymbol{{b}}^{\mathrm{2}} }{\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right)^{\mathrm{2}} }\:\:\:\:\:...\left(\boldsymbol{{ii}}\right) \\ $$$${As}\:\:\:\:{OT}=\mathrm{1}\:\:{so}\:\:\:\boldsymbol{{x}}_{\boldsymbol{{T}}} ^{\mathrm{2}} +\boldsymbol{{y}}_{\boldsymbol{{T}}} ^{\mathrm{2}} \:=\:\mathrm{1}\:\:\: \\ $$$$\Rightarrow\:\:{a}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{\left({a}+{b}\right)^{\mathrm{2}} }+\frac{{b}^{\mathrm{4}} }{\left({a}+{b}\right)^{\mathrm{2}} }\:=\mathrm{1}\:\:...\left({iii}\right) \\ $$$$\:\:\:\:\:\:\left({a}^{\mathrm{2}} −\mathrm{1}\right)=\frac{{b}^{\mathrm{2}} \left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}{\left({a}+{b}\right)^{\mathrm{2}} } \\ $$$${one}\:{solution}\:{of}\:{this}\:{eq}.\:{is} \\ $$$${a}={b}=\mathrm{1}\:\:\:,\:{otherwise} \\ $$$$\:\:\:\:\:\:{a}^{\mathrm{2}} −\mathrm{1}\:=\:\frac{{b}^{\mathrm{2}} \left({a}−{b}\right)}{{a}+{b}}\:\:\:\:\: \\ $$$${if}\:{a}={br}\:\:{then} \\ $$$$\:\:{b}^{\mathrm{2}} {r}^{\mathrm{2}} −\mathrm{1}={b}^{\mathrm{2}} \left(\frac{{r}−\mathrm{1}}{{r}+\mathrm{1}}\right) \\ $$$$\:\:\:\:{b}^{\mathrm{2}} \left({r}^{\mathrm{2}} −\frac{{r}−\mathrm{1}}{{r}+\mathrm{1}}\right)=\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:...\left({iv}\right) \\ $$$${And}\:{as}\:\left(\:\:\frac{{PT}}{{OT}}\:=\:\frac{{BP}}{{OB}}\:\:\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\frac{{x}_{{T}} ^{\mathrm{2}} +\left[\left({a}+{b}\right)−{y}_{{T}} \right]^{\mathrm{2}} }{\mathrm{1}}\:=\:\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:{a}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{\left({a}+{b}\right)^{\mathrm{2}} }+\left({a}+{b}\right)^{\mathrm{2}} +{y}_{{T}} ^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{2}\left({a}+{b}\right){y}_{{T}} \:=\:\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} } \\ $$$$\Rightarrow\:{a}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{\left({a}+{b}\right)^{\mathrm{2}} }+\left({a}+{b}\right)^{\mathrm{2}} +\frac{{b}^{\mathrm{4}} }{\left({a}+{b}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{2}{b}^{\mathrm{2}} \:=\:\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\:\:\:\:\:\:...\left({v}\right) \\ $$$${using}\:\left({iii}\right)\:\:{in}\:{above}\:{eq}.\:\left({v}\right) \\ $$$$\:\:\:\:\:\mathrm{1}+\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right)^{\mathrm{2}} −\mathrm{2}\boldsymbol{{b}}^{\mathrm{2}} \:=\:\frac{\boldsymbol{{a}}^{\mathrm{2}} }{\boldsymbol{{b}}^{\mathrm{2}} } \\ $$$${again}\:{with}\:{a}={br} \\ $$$$\:\:\:\:\:\mathrm{1}+{b}^{\mathrm{2}} \left({r}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:{b}^{\mathrm{2}} \left({r}^{\mathrm{2}} +\mathrm{2}{r}−\mathrm{1}\right)={r}^{\mathrm{2}} −\mathrm{1}\:\:\:\:...\left({vi}\right) \\ $$$${comparing}\:\left({iv}\right)\:{and}\:\left({vi}\right) \\ $$$$\Rightarrow\:\:\:\frac{{r}^{\mathrm{2}} +\mathrm{2}{r}−\mathrm{1}}{{r}^{\mathrm{2}} −\frac{{r}−\mathrm{1}}{{r}+\mathrm{1}}}\:=\:\frac{{r}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}} \\ $$$$\Rightarrow\:\:\:\:\frac{\mathrm{2}{r}}{{r}^{\mathrm{2}} −\mathrm{1}−\frac{{r}−\mathrm{1}}{{r}+\mathrm{1}}}\:=\:{r}^{\mathrm{2}} −\mathrm{1} \\ $$$$\:\mathrm{2}{r}\left({r}+\mathrm{1}\right)=\left({r}^{\mathrm{2}} −\mathrm{1}\right)\left[\left({r}^{\mathrm{2}} −\mathrm{1}\right)\left({r}+\mathrm{1}\right)−\left({r}−\mathrm{1}\right)\right] \\ $$$$\Rightarrow\:\:\mathrm{2}{r}=\left({r}−\mathrm{1}\right)^{\mathrm{2}} \left[\left({r}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}\right] \\ $$$$\Rightarrow\:\:\:\mathrm{2}{r}\:=\:\left({r}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} −\left({r}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$${or}\:\:\:\boldsymbol{{r}}^{\mathrm{4}} −\mathrm{3}\boldsymbol{{r}}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\:\:\:\:{r}=\:\sqrt{\mathrm{3}}\:\:\:\:\:\:\left({valid}\:{answer}\right) \\ $$$$\:\:\:{Now}\:{from}\:\left({vi}\right)\:{we}\:{have} \\ $$$$\:\:\:\boldsymbol{{b}}^{\mathrm{2}} \:=\:\frac{\boldsymbol{{r}}^{\mathrm{2}} −\mathrm{1}}{\boldsymbol{{r}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{{r}}−\mathrm{1}}\:=\:\frac{\mathrm{2}}{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{3}}}\:=\:\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{3}}} \\ $$$$\:\:\:=\:\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:{While}\:\:\boldsymbol{{a}}^{\mathrm{2}} \:=\:\boldsymbol{{b}}^{\mathrm{2}} \boldsymbol{{r}}^{\mathrm{2}} \:=\:\frac{\mathrm{3}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)}{\mathrm{2}} \\ $$$${Ellipse}\:{eq}.\:{is}\:{thus} \\ $$$$\:\:\:\:\:\:\frac{\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{3}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)}+\frac{\mathrm{2}{y}^{\mathrm{2}} }{\sqrt{\mathrm{3}}−\mathrm{1}}\:=\mathrm{1} \\ $$$${or}\:\:\:\:\underset{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_} {\:} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}{x}^{\mathrm{2}} +\mathrm{6}{y}^{\mathrm{2}} \:=\:\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{3}\:\:\: \\ $$$$\:\:\:\:\:\:\overset{\:\:\:\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\:.} {\:} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 13/Jul/18
$${bah}...{very}\:{good}...{excellent}... \\ $$
Commented by ajfour last updated on 13/Jul/18
$${thanks}\:{sir}\:! \\ $$
Commented by MrW3 last updated on 13/Jul/18
$${awesome}! \\ $$