Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 39891 by math khazana by abdo last updated on 13/Jul/18

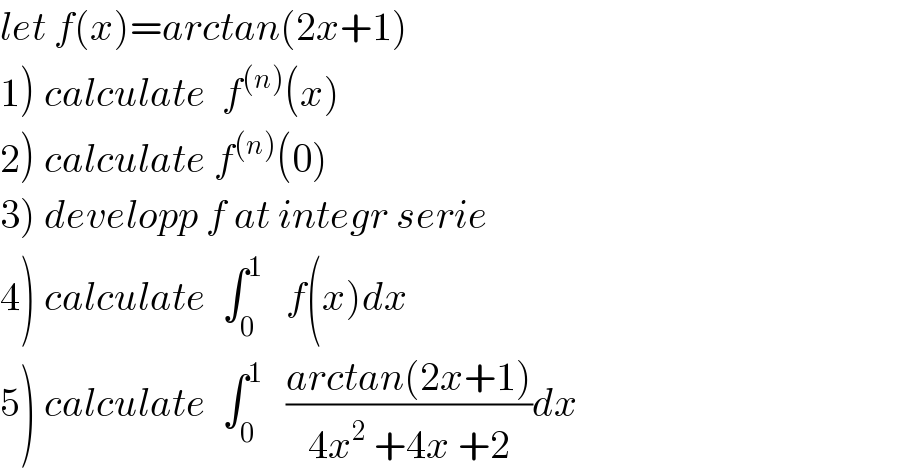
let f(x)=arctan(2x+1) 1) calculate f^((n)) (x) 2) calculate f^((n)) (0) 3) developp f at integr serie 4) calculate ∫_0 ^1 f(x)dx 5) calculate ∫_0 ^1 ((arctan(2x+1))/(4x^2 +4x +2))dx

$${let}\:{f}\left({x}\right)={arctan}\left(\mathrm{2}{x}+\mathrm{1}\right) \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:\:{f}^{\left({n}\right)} \left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:{f}^{\left({n}\right)} \left(\mathrm{0}\right) \\ $$$$\left.\mathrm{3}\right)\:{developp}\:{f}\:{at}\:{integr}\:{serie} \\ $$$$\left.\mathrm{4}\right)\:{calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:{f}\left({x}\right){dx} \\ $$$$\left.\mathrm{5}\right)\:{calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{arctan}\left(\mathrm{2}{x}+\mathrm{1}\right)}{\mathrm{4}{x}^{\mathrm{2}} \:+\mathrm{4}{x}\:+\mathrm{2}}{dx} \\ $$

Commented by maxmathsup by imad last updated on 13/Jul/18

1) we have f^′ (x)= (2/(1+(2x+1)^2 )) ⇒f^((n)) (x)=2 ((1/((2x+1)^2 +1)))^((n−1)) let w(x)= (1/((2x+1)^2 +1)) .let decompose w inside C(x) w(x)= (1/((2x+1−i)(2x+1 +i))) = (1/(4(x +((1−i)/2))(x +((1+i)/2)))) =(1/(4(x +(1/(√2))e^(−((iπ)/4)) )(x +(1/(√2))e^(i(π/4)) ))) = (a/(x+(1/(√2))e^(−((iπ)/4)) )) +(b/(x+(1/(√2))e^((iπ)/4) )) a =lim_(x→−(1/(√2))e^(−((iπ)/4)) ) (x +(1/(√2))e^(−((iπ)/4)) )w(x)= (1/(4(1/(√2))(e^((iπ)/4) −e^(−((iπ)/4)) ))) = ((√2)/(4(2i(1/(√2))))) = (1/(4i)) b =lim_(x→−(1/(√2)) e^(i(π/4)) ) (x+ (1/(√2)) e^((iπ)/4) )w(x)= (1/(4(1/((√2) ))(−e^((iπ)/4) +e^(−((iπ)/4)) ))) =((√2)/(−4(2i(1/(√2))))) = ((−2)/(8i)) = −(1/(4i)) ⇒w(x)= (1/(4i)){ (1/(x+(1/(√2))e^(−((iπ)/4)) )) −(1/(x +(1/(√2))e^((iπ)/4) ))} ⇒ w^((n−1)) = (1/(4i)){ (((−1)^(n−1) (n−1)!)/((x +(1/(√2))e^(−((iπ)/4)) )^n )) −(((−1)^(n−1) (n−1)!)/((x +(1/(√2))e^((iπ)/4) )^n ))} ⇒ f^((n)) (x) =2 w^((n−1)) (x) = (((−1)^(n−1) (n−1)!)/(2i)){ (1/((x +(1/(√2))e^(−((iπ)/4)) )^n )) −(1/((x +(1/(√2))e^((iπ)/4) )^n ))}.

$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}^{'} \left({x}\right)=\:\frac{\mathrm{2}}{\mathrm{1}+\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow{f}^{\left({n}\right)} \left({x}\right)=\mathrm{2}\:\:\left(\frac{\mathrm{1}}{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}\right)^{\left({n}−\mathrm{1}\right)} \\ $$$${let}\:{w}\left({x}\right)=\:\frac{\mathrm{1}}{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}}\:\:.{let}\:{decompose}\:{w}\:{inside}\:{C}\left({x}\right) \\ $$$${w}\left({x}\right)=\:\frac{\mathrm{1}}{\left(\mathrm{2}{x}+\mathrm{1}−{i}\right)\left(\mathrm{2}{x}+\mathrm{1}\:+{i}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{4}\left({x}\:+\frac{\mathrm{1}−{i}}{\mathrm{2}}\right)\left({x}\:+\frac{\mathrm{1}+{i}}{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\left({x}\:+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\left({x}\:\:+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{e}^{{i}\frac{\pi}{\mathrm{4}}} \right)}\:=\:\frac{{a}}{{x}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} }\:+\frac{{b}}{{x}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{e}^{\frac{{i}\pi}{\mathrm{4}}} } \\ $$$${a}\:={lim}_{{x}\rightarrow−\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} } \:\:\:\left({x}\:+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right){w}\left({x}\right)=\:\:\frac{\mathrm{1}}{\mathrm{4}\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\left({e}^{\frac{{i}\pi}{\mathrm{4}}} \:−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)}\:=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{4}\left(\mathrm{2}{i}\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{4}{i}} \\ $$$${b}\:={lim}_{{x}\rightarrow−\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:{e}^{{i}\frac{\pi}{\mathrm{4}}} } \:\:\:\left({x}+\:\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \right){w}\left({x}\right)=\:\:\frac{\mathrm{1}}{\mathrm{4}\frac{\mathrm{1}}{\sqrt{\mathrm{2}}\:}\left(−{e}^{\frac{{i}\pi}{\mathrm{4}}} \:+{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)}\:=\frac{\sqrt{\mathrm{2}}}{−\mathrm{4}\left(\mathrm{2}{i}\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\right)} \\ $$$$=\:\frac{−\mathrm{2}}{\mathrm{8}{i}}\:=\:−\frac{\mathrm{1}}{\mathrm{4}{i}}\:\Rightarrow{w}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{4}{i}}\left\{\:\:\:\:\frac{\mathrm{1}}{{x}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} }\:−\frac{\mathrm{1}}{{x}\:+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{e}^{\frac{{i}\pi}{\mathrm{4}}} }\right\}\:\Rightarrow \\ $$$${w}^{\left({n}−\mathrm{1}\right)} =\:\frac{\mathrm{1}}{\mathrm{4}{i}}\left\{\:\:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\left({x}\:+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)^{{n}} }\:−\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\left({x}\:+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)^{{n}} }\right\}\:\Rightarrow \\ $$$${f}^{\left({n}\right)} \left({x}\right)\:=\mathrm{2}\:{w}^{\left({n}−\mathrm{1}\right)} \left({x}\right)\:=\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\mathrm{2}{i}}\left\{\:\:\:\frac{\mathrm{1}}{\left({x}\:+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)^{{n}} }\:−\frac{\mathrm{1}}{\left({x}\:+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)^{{n}} }\right\}. \\ $$

Commented by maxmathsup by imad last updated on 13/Jul/18

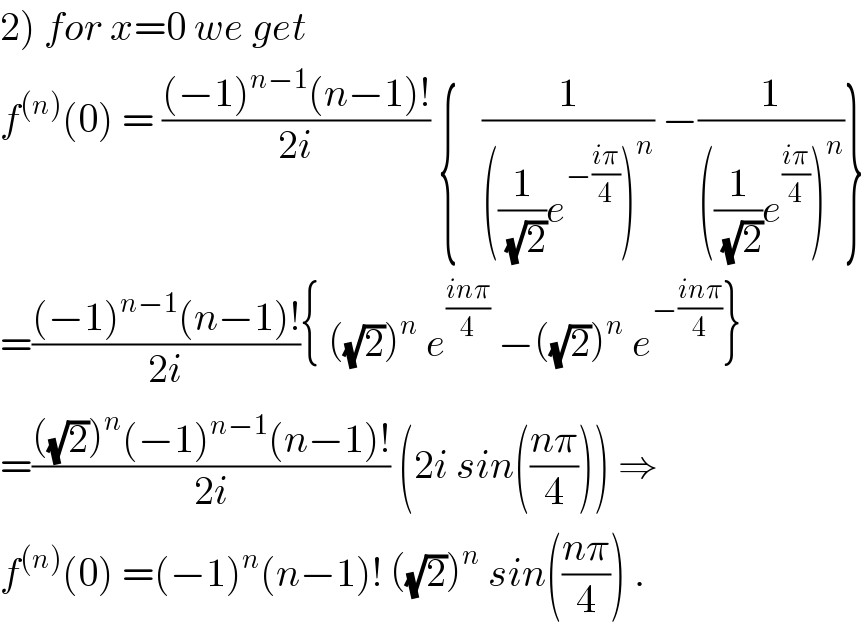
2) for x=0 we get f^((n)) (0) = (((−1)^(n−1) (n−1)!)/(2i)) { (1/(((1/(√2))e^(−((iπ)/4)) )^n )) −(1/(((1/(√2))e^((iπ)/4) )^n ))} =(((−1)^(n−1) (n−1)!)/(2i)){ ((√2))^n e^((inπ)/4) −((√2))^n e^(−((inπ)/4)) } =((((√2))^n (−1)^(n−1) (n−1)!)/(2i)) (2i sin(((nπ)/4))) ⇒ f^((n)) (0) =(−1)^n (n−1)! ((√2))^n sin(((nπ)/4)) .

$$\left.\mathrm{2}\right)\:{for}\:{x}=\mathrm{0}\:{we}\:{get}\: \\ $$$${f}^{\left({n}\right)} \left(\mathrm{0}\right)\:=\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\mathrm{2}{i}}\:\left\{\:\:\:\frac{\mathrm{1}}{\left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)^{{n}} }\:−\frac{\mathrm{1}}{\left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)^{{n}} }\right\} \\ $$$$=\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\mathrm{2}{i}}\left\{\:\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{e}^{\frac{{in}\pi}{\mathrm{4}}} \:−\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{e}^{−\frac{{in}\pi}{\mathrm{4}}} \right\} \\ $$$$=\frac{\left(\sqrt{\mathrm{2}}\right)^{{n}} \left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\mathrm{2}{i}}\:\left(\mathrm{2}{i}\:{sin}\left(\frac{{n}\pi}{\mathrm{4}}\right)\right)\:\Rightarrow \\ $$$${f}^{\left({n}\right)} \left(\mathrm{0}\right)\:=\left(−\mathrm{1}\right)^{{n}} \left({n}−\mathrm{1}\right)!\:\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{sin}\left(\frac{{n}\pi}{\mathrm{4}}\right)\:. \\ $$

Commented by maxmathsup by imad last updated on 14/Jul/18

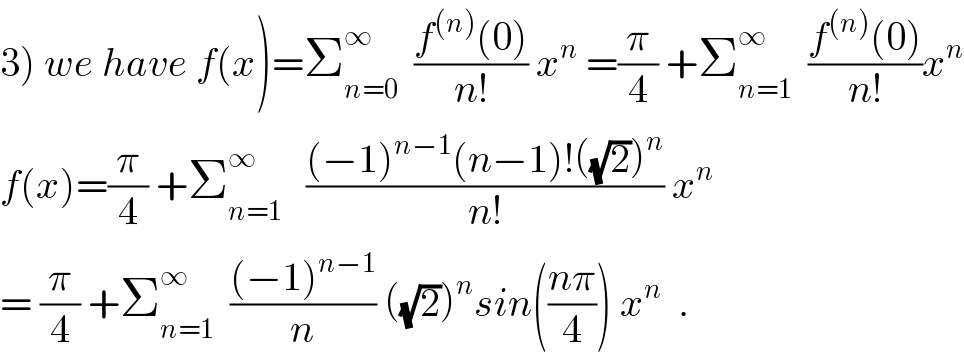
3) we have f(x)=Σ_(n=0) ^∞ ((f^((n)) (0))/(n!)) x^n =(π/4) +Σ_(n=1) ^∞ ((f^((n)) (0))/(n!))x^n f(x)=(π/4) +Σ_(n=1) ^∞ (((−1)^(n−1) (n−1)!((√2))^n )/(n!)) x^n = (π/4) +Σ_(n=1) ^∞ (((−1)^(n−1) )/n) ((√2))^n sin(((nπ)/4)) x^n .

$$\left.\mathrm{3}\right)\:{we}\:{have}\:{f}\left({x}\right)=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{{f}^{\left({n}\right)} \left(\mathrm{0}\right)}{{n}!}\:{x}^{{n}} \:=\frac{\pi}{\mathrm{4}}\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{f}^{\left({n}\right)} \left(\mathrm{0}\right)}{{n}!}{x}^{{n}} \\ $$$${f}\left({x}\right)=\frac{\pi}{\mathrm{4}}\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!\left(\sqrt{\mathrm{2}}\right)^{{n}} }{{n}!}\:{x}^{{n}} \\ $$$$=\:\frac{\pi}{\mathrm{4}}\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:\left(\sqrt{\mathrm{2}}\right)^{{n}} {sin}\left(\frac{{n}\pi}{\mathrm{4}}\right)\:{x}^{{n}} \:\:. \\ $$

Commented by maxmathsup by imad last updated on 14/Jul/18

4) ∫_0 ^1 f(x)dx = ∫_0 ^1 arctan(2x+1)dx by parts u^′ =1 and v=arctan(2x+1) ∫_0 ^1 arctan(2x+1)dx = [x arctan(2x+1)]_0 ^1 − ∫_0 ^1 x (2/(1+(2x+1)^2 ))dx = arctan(3) − ∫_0 ^1 ((2x)/(4x^2 +4x +2)) dx but ∫_0 ^1 ((2x)/(4x^2 +4x +2))dx = ∫_0 ^1 (x/(2x^2 +2x +1))dx =(1/4) ∫_0 ^1 ((4x +2−2)/(2x^2 +2x +1))dx = (1/4) ∫_0 ^1 ((4x+2)/(2x^2 +2x+1)) dx −(1/2) ∫_0 ^1 (dx/(2(x^2 +x +(1/2)))) =(1/4)[ln∣2x^2 +2x +1∣]_0 ^1 −(1/4) ∫_0 ^1 (dx/(x^2 +2(1/2)x +(1/4)+(1/4))) =(1/4)ln(5) −(1/4) ∫_0 ^1 (dx/((x+(1/2))^2 +(1/4))) ( ch .x+(1/2)=(1/2)t) =(1/4)ln(5) −(1/4) ∫_0 ^1 (1/((1/4)(1+t^2 ))) (dt/2) =((ln(5))/4) −(1/2) (π/4) =((ln(5))/4) −(π/8) ⇒ ∫_0 ^1 f(x)dx = arctan(3) −((ln(5))/4) +(π/8) .

$$\left.\mathrm{4}\right)\:\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{arctan}\left(\mathrm{2}{x}+\mathrm{1}\right){dx}\:\:{by}\:{parts}\:{u}^{'} =\mathrm{1}\:{and}\:{v}={arctan}\left(\mathrm{2}{x}+\mathrm{1}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{arctan}\left(\mathrm{2}{x}+\mathrm{1}\right){dx}\:=\:\left[{x}\:{arctan}\left(\mathrm{2}{x}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}\:\frac{\mathrm{2}}{\mathrm{1}+\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$=\:{arctan}\left(\mathrm{3}\right)\:−\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\frac{\mathrm{2}{x}}{\mathrm{4}{x}^{\mathrm{2}} \:+\mathrm{4}{x}\:+\mathrm{2}}\:{dx}\:\:{but} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\frac{\mathrm{2}{x}}{\mathrm{4}{x}^{\mathrm{2}} \:+\mathrm{4}{x}\:+\mathrm{2}}{dx}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{x}}{\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{2}{x}\:+\mathrm{1}}{dx}\:=\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{4}{x}\:+\mathrm{2}−\mathrm{2}}{\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{2}{x}\:+\mathrm{1}}{dx} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{4}{x}+\mathrm{2}}{\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{2}{x}+\mathrm{1}}\:{dx}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{dx}}{\mathrm{2}\left({x}^{\mathrm{2}} \:+{x}\:+\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left[{ln}\mid\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{2}{x}\:+\mathrm{1}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} \:\:−\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\mathrm{2}\frac{\mathrm{1}}{\mathrm{2}}{x}\:+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\mathrm{5}\right)\:−\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\:\frac{{dx}}{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{4}}}\:\:\left(\:{ch}\:.{x}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}{t}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\mathrm{5}\right)\:\:−\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\:\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}\:\frac{{dt}}{\mathrm{2}}\:=\frac{{ln}\left(\mathrm{5}\right)}{\mathrm{4}}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\pi}{\mathrm{4}}\:=\frac{{ln}\left(\mathrm{5}\right)}{\mathrm{4}}\:−\frac{\pi}{\mathrm{8}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}\:=\:{arctan}\left(\mathrm{3}\right)\:−\frac{{ln}\left(\mathrm{5}\right)}{\mathrm{4}}\:+\frac{\pi}{\mathrm{8}}\:. \\ $$$$ \\ $$

Commented by maxmathsup by imad last updated on 14/Jul/18

5) we have ∫_0 ^1 ((arctan(2x+1))/(4x^2 +4x +2))dx = ∫_0 ^1 ((arctan(2x+1))/((2x+1)^2 +1)) and by parts u^′ = (1/((2x+1)^2 +1)) and v=arctan(2x+1) we get ∫_0 ^1 ((arctan(2x+1))/((2x+1)^2 +1)) dx = [ (1/2)arctan(2x+1).arctan(2x+1)]_0 ^1 −∫_0 ^1 (1/2) arctan(2x+1).(2/((2x+1)^2 +1)) dx =(1/2) (arctan(3))^2 −(π^2 /(32)) −∫_0 ^1 ((arctan(2x+1))/((2x+1)^2 +1)) ⇒ ∫_0 ^1 ((arctan(2x+1))/((2x+1)^2 +1)) dx = (1/4) (arctan(3))^2 −(π^2 /(64)) .

$$\left.\mathrm{5}\right)\:{we}\:{have}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{arctan}\left(\mathrm{2}{x}+\mathrm{1}\right)}{\mathrm{4}{x}^{\mathrm{2}} \:+\mathrm{4}{x}\:+\mathrm{2}}{dx}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{arctan}\left(\mathrm{2}{x}+\mathrm{1}\right)}{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}}\:{and}\:{by}\:{parts} \\ $$$${u}^{'} \:=\:\frac{\mathrm{1}}{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}}\:{and}\:{v}={arctan}\left(\mathrm{2}{x}+\mathrm{1}\right)\:{we}\:{get} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{arctan}\left(\mathrm{2}{x}+\mathrm{1}\right)}{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}}\:{dx}\:=\:\left[\:\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\mathrm{2}{x}+\mathrm{1}\right).{arctan}\left(\mathrm{2}{x}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{1}}{\mathrm{2}}\:{arctan}\left(\mathrm{2}{x}+\mathrm{1}\right).\frac{\mathrm{2}}{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}}\:{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\left({arctan}\left(\mathrm{3}\right)\right)^{\mathrm{2}} \:−\frac{\pi^{\mathrm{2}} }{\mathrm{32}}\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{arctan}\left(\mathrm{2}{x}+\mathrm{1}\right)}{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{arctan}\left(\mathrm{2}{x}+\mathrm{1}\right)}{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}}\:{dx}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\:\left({arctan}\left(\mathrm{3}\right)\right)^{\mathrm{2}} \:−\frac{\pi^{\mathrm{2}} }{\mathrm{64}}\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com