
Question and Answers Forum
Question Number 40008 by math khazana by abdo last updated on 15/Jul/18
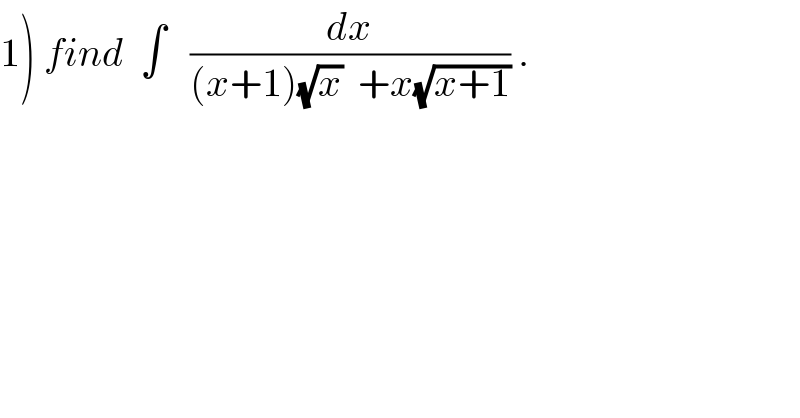
Commented by abdo mathsup 649 cc last updated on 15/Jul/18
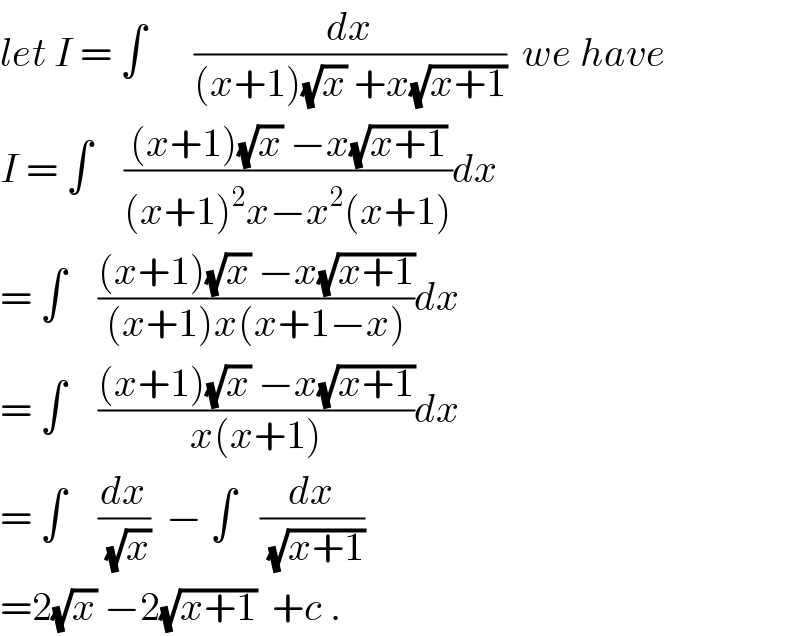
Answered by ajfour last updated on 15/Jul/18
![I=∫(([(x+1)(√x)−x(√(x+1)) ]dx)/(x(x+1)[x+1−x])) =∫(dx/(√x))−∫(dx/(√(x+1))) =2(√x)−2(√(x+1))+c .](Q40011.png)
| ||
Question and Answers Forum | ||
Question Number 40008 by math khazana by abdo last updated on 15/Jul/18 | ||
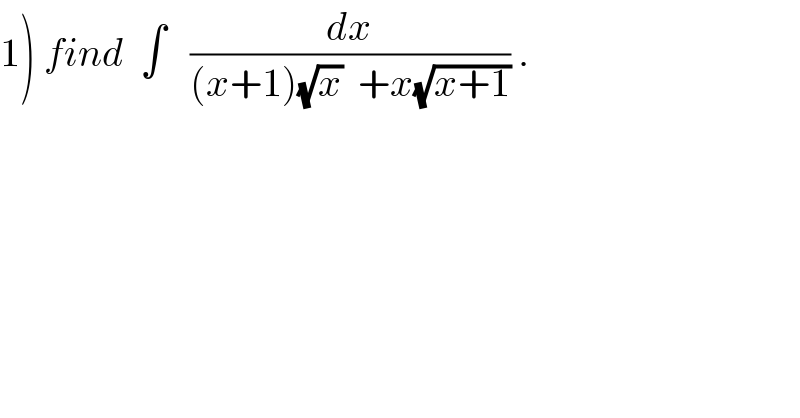 | ||
Commented by abdo mathsup 649 cc last updated on 15/Jul/18 | ||
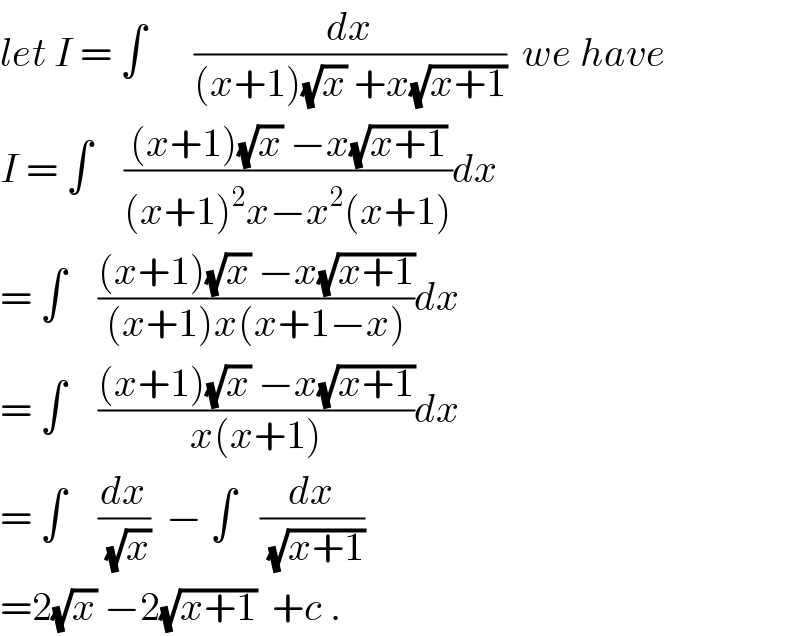 | ||
Answered by ajfour last updated on 15/Jul/18 | ||
![I=∫(([(x+1)(√x)−x(√(x+1)) ]dx)/(x(x+1)[x+1−x])) =∫(dx/(√x))−∫(dx/(√(x+1))) =2(√x)−2(√(x+1))+c .](Q40011.png) | ||
| ||