
Question and Answers Forum
Question Number 40043 by abdo mathsup 649 cc last updated on 15/Jul/18
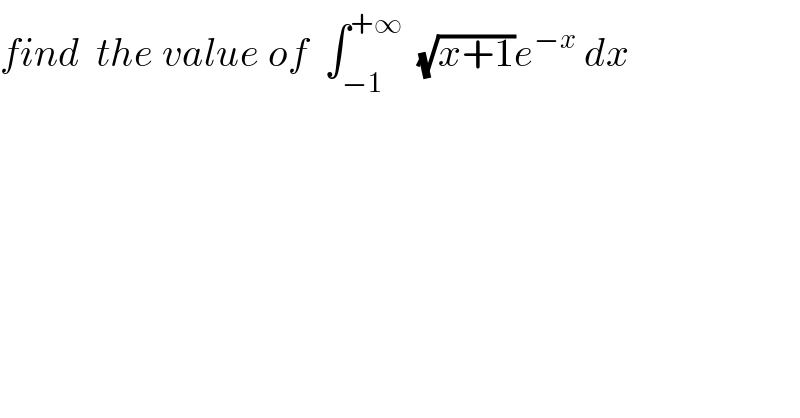
Answered by prof Abdo imad last updated on 22/Jul/18
![changement (√(x+1))=t give x+1=t^2 I = ∫_0 ^∞ t e^(−(t^2 −1)) 2t dt =2e ∫_0 ^∞ t^2 e^(−t^2 ) dt and by partsu^′ =t e^(−t^2 ) v=t I =2e{ [−(1/2) e^(−t^2 ) t]_0 ^(+∞) +∫_0 ^∞ (1/2) e^(−t^2 ) dt} = e ∫_0 ^∞ e^(−t^2 ) dt = e ((√π)/2) ⇒ I = (e/2)(√π).](Q40488.png)
| ||
Question and Answers Forum | ||
Question Number 40043 by abdo mathsup 649 cc last updated on 15/Jul/18 | ||
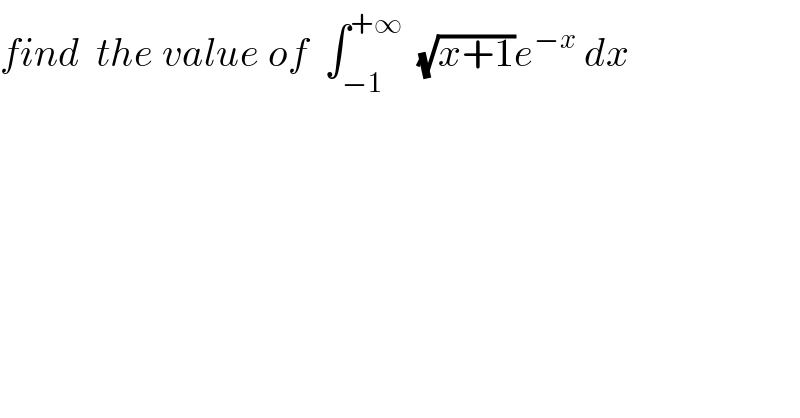 | ||
Answered by prof Abdo imad last updated on 22/Jul/18 | ||
![changement (√(x+1))=t give x+1=t^2 I = ∫_0 ^∞ t e^(−(t^2 −1)) 2t dt =2e ∫_0 ^∞ t^2 e^(−t^2 ) dt and by partsu^′ =t e^(−t^2 ) v=t I =2e{ [−(1/2) e^(−t^2 ) t]_0 ^(+∞) +∫_0 ^∞ (1/2) e^(−t^2 ) dt} = e ∫_0 ^∞ e^(−t^2 ) dt = e ((√π)/2) ⇒ I = (e/2)(√π).](Q40488.png) | ||
| ||