
Previous in Relation and Functions Next in Relation and Functions
Question Number 40106 by maxmathsup by imad last updated on 15/Jul/18
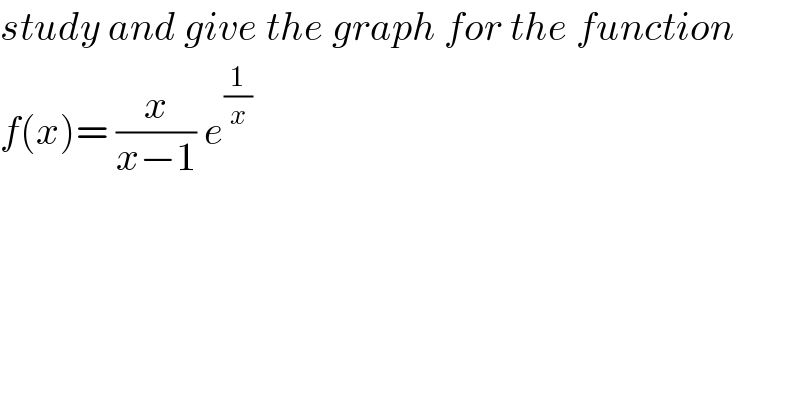
$${study}\:{and}\:{give}\:{the}\:{graph}\:{for}\:{the}\:{function} \\ $$$${f}\left({x}\right)=\:\frac{{x}}{{x}−\mathrm{1}}\:{e}^{\frac{\mathrm{1}}{{x}}} \\ $$
Answered by math khazana by abdo last updated on 28/Jul/18
![D_f =R−{0,1} =]−∞,0[∪]0,1[∪]1,+∞[ lim_(x→−∞) f(x)=lim_(x→−∞) (x/(x−1))e^(1/x) =1 y=1 is assymtote at −∞ lim_(x→+∞) f(x)=lim_(x→+∞) (x/(x−1)) e^(1/x) =1 so y=1 is assymptote at+∞ lim_(x→1^− ) f(x) =−∞ and lim_(x→1^+ ) f(x)= +∞ lim_(x→0^+ ) f(x)=lim_(x→0^+ ) (x/(x−1)) e^(1/x) chang=(1/x)=t =lim_(t→+∞) (1/(t((1/t)−1))) e^t =lim_(t→+∞) (1/(1−t)) e^t =lim_(t→+∞) (e^t /t) (1/((1/t)−1)) =−∞ lim_(x→0^− ) f(x) =lim_(x→0^− ) (x/(x−1)) e^(1/x) (ch.(1/x)=t) =lim_(t→−∞) (1/(t((1/t)−1))) e^t =lim_(t→−∞) −(e^t /t)=0 we have f^′ (x)=((x/(x−1)))^′ e^(1/x) +((x/(x−1)))(e^(1/x) )^′ = −(1/((x−1)^2 )) e^(1/x) −(1/x^2 )((x/(x−1)))e^(1/x) =−(1/((x−1)^2 )) e^(1/x) − (1/(x(x−1))) e^(1/x) =−(1/((x−1))) e^(1/x) { (1/x) +1} =−((x+1)/x)(1/((x−1)))e^(1/x) =−((x+1)/(x(x−1))) e^(1/x) ....be continued...](Q40863.png)
$$\left.{D}_{{f}} ={R}−\left\{\mathrm{0},\mathrm{1}\right\}\:=\right]−\infty,\mathrm{0}\left[\cup\right]\mathrm{0},\mathrm{1}\left[\cup\right]\mathrm{1},+\infty\left[\right. \\ $$$$ \\ $$$${lim}_{{x}\rightarrow−\infty} {f}\left({x}\right)={lim}_{{x}\rightarrow−\infty} \frac{{x}}{{x}−\mathrm{1}}{e}^{\frac{\mathrm{1}}{{x}}} \:=\mathrm{1} \\ $$$${y}=\mathrm{1}\:{is}\:{assymtote}\:{at}\:−\infty \\ $$$${lim}_{{x}\rightarrow+\infty} \:{f}\left({x}\right)={lim}_{{x}\rightarrow+\infty} \:\frac{{x}}{{x}−\mathrm{1}}\:{e}^{\frac{\mathrm{1}}{{x}}} \:=\mathrm{1}\:{so} \\ $$$${y}=\mathrm{1}\:{is}\:{assymptote}\:{at}+\infty \\ $$$${lim}_{{x}\rightarrow\mathrm{1}^{−} } \:\:{f}\left({x}\right)\:\:=−\infty\:\:{and}\:{lim}_{{x}\rightarrow\mathrm{1}^{+} } \:\:{f}\left({x}\right)=\:+\infty \\ $$$${lim}_{{x}\rightarrow\mathrm{0}^{+} } \:\:\:{f}\left({x}\right)={lim}_{{x}\rightarrow\mathrm{0}^{+} } \:\:\:\frac{{x}}{{x}−\mathrm{1}}\:{e}^{\frac{\mathrm{1}}{{x}}} \:{chang}=\frac{\mathrm{1}}{{x}}={t} \\ $$$$={lim}_{{t}\rightarrow+\infty} \:\:\:\:\:\frac{\mathrm{1}}{{t}\left(\frac{\mathrm{1}}{{t}}−\mathrm{1}\right)}\:{e}^{{t}} ={lim}_{{t}\rightarrow+\infty} \:\frac{\mathrm{1}}{\mathrm{1}−{t}}\:{e}^{{t}} \:\: \\ $$$$={lim}_{{t}\rightarrow+\infty} \:\:\:\frac{{e}^{{t}} }{{t}}\:\frac{\mathrm{1}}{\frac{\mathrm{1}}{{t}}−\mathrm{1}}\:=−\infty \\ $$$${lim}_{{x}\rightarrow\mathrm{0}^{−} } \:\:\:{f}\left({x}\right)\:={lim}_{{x}\rightarrow\mathrm{0}^{−} } \:\:\:\frac{{x}}{{x}−\mathrm{1}}\:{e}^{\frac{\mathrm{1}}{{x}}} \left({ch}.\frac{\mathrm{1}}{{x}}={t}\right) \\ $$$$={lim}_{{t}\rightarrow−\infty} \:\:\:\:\frac{\mathrm{1}}{{t}\left(\frac{\mathrm{1}}{{t}}−\mathrm{1}\right)}\:{e}^{{t}} \:={lim}_{{t}\rightarrow−\infty} −\frac{{e}^{{t}} }{{t}}=\mathrm{0} \\ $$$${we}\:{have}\:{f}^{'} \left({x}\right)=\left(\frac{{x}}{{x}−\mathrm{1}}\right)^{'} {e}^{\frac{\mathrm{1}}{{x}}} \:+\left(\frac{{x}}{{x}−\mathrm{1}}\right)\left({e}^{\frac{\mathrm{1}}{{x}}} \right)^{'} \\ $$$$=\:\:\:\:−\frac{\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\:{e}^{\frac{\mathrm{1}}{{x}}} \:−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\left(\frac{{x}}{{x}−\mathrm{1}}\right){e}^{\frac{\mathrm{1}}{{x}}} \\ $$$$=−\frac{\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\:{e}^{\frac{\mathrm{1}}{{x}}} \:−\:\frac{\mathrm{1}}{{x}\left({x}−\mathrm{1}\right)}\:{e}^{\frac{\mathrm{1}}{{x}}} \\ $$$$=−\frac{\mathrm{1}}{\left({x}−\mathrm{1}\right)}\:{e}^{\frac{\mathrm{1}}{{x}}} \left\{\:\frac{\mathrm{1}}{{x}}\:+\mathrm{1}\right\}\:=−\frac{{x}+\mathrm{1}}{{x}}\frac{\mathrm{1}}{\left({x}−\mathrm{1}\right)}{e}^{\frac{\mathrm{1}}{{x}}} \\ $$$$=−\frac{{x}+\mathrm{1}}{{x}\left({x}−\mathrm{1}\right)}\:{e}^{\frac{\mathrm{1}}{{x}}} \:\:\:....{be}\:{continued}... \\ $$$$\:\:\:\: \\ $$
