Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 40113 by maxmathsup by imad last updated on 15/Jul/18

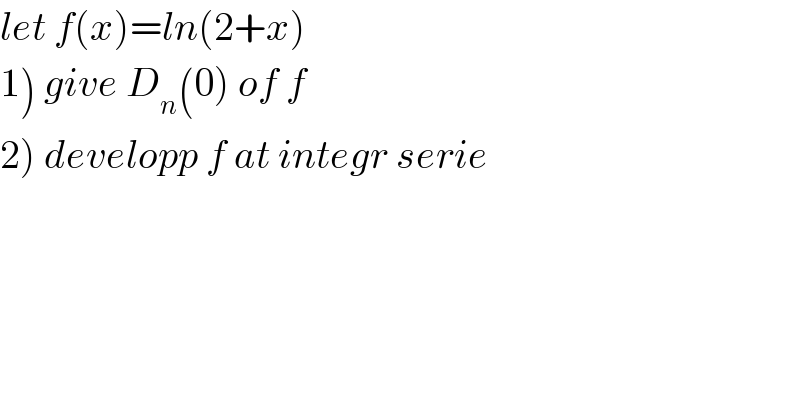
let f(x)=ln(2+x) 1) give D_n (0) of f 2) developp f at integr serie

$${let}\:{f}\left({x}\right)={ln}\left(\mathrm{2}+{x}\right) \\ $$$$\left.\mathrm{1}\right)\:{give}\:{D}_{{n}} \left(\mathrm{0}\right)\:{of}\:{f} \\ $$$$\left.\mathrm{2}\right)\:{developp}\:{f}\:{at}\:{integr}\:{serie} \\ $$

Commented by prof Abdo imad last updated on 17/Jul/18

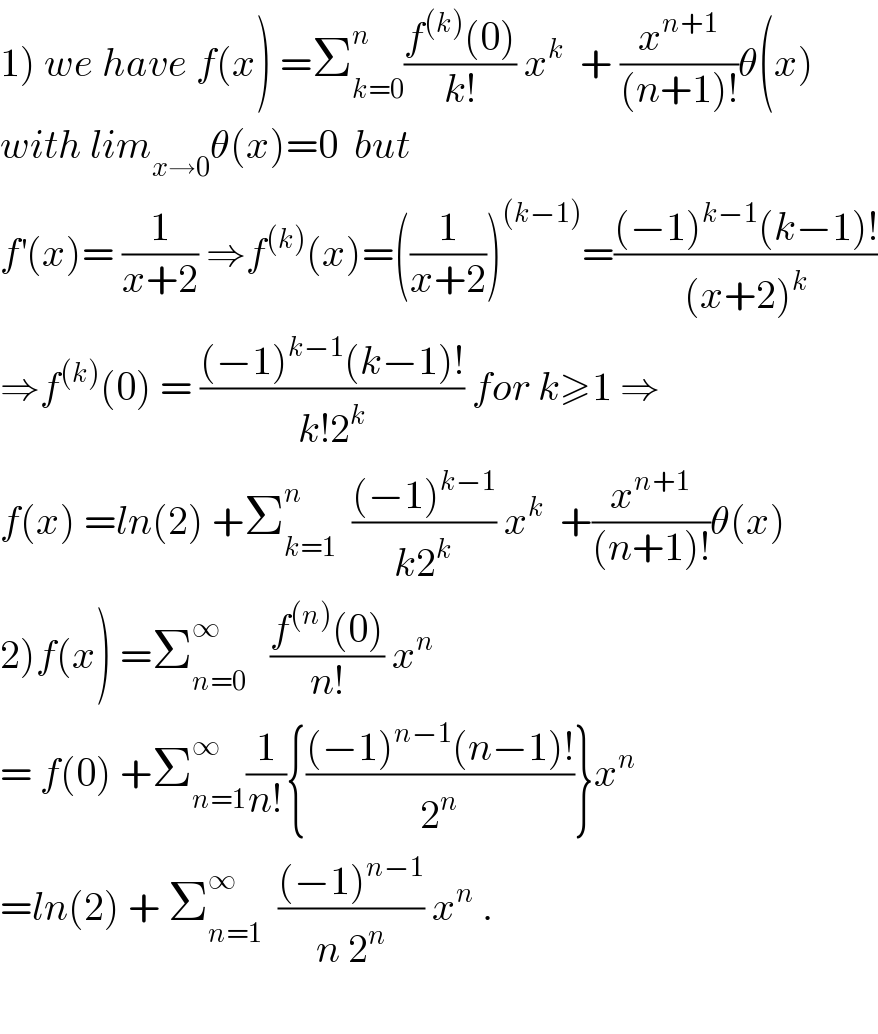
1) we have f(x) =Σ_(k=0) ^n ((f^((k)) (0))/(k!)) x^k + (x^(n+1) /((n+1)!))θ(x) with lim_(x→0) θ(x)=0 but f^′ (x)= (1/(x+2)) ⇒f^((k)) (x)=((1/(x+2)))^((k−1)) =(((−1)^(k−1) (k−1)!)/((x+2)^k )) ⇒f^((k)) (0) = (((−1)^(k−1) (k−1)!)/(k!2^k )) for k≥1 ⇒ f(x) =ln(2) +Σ_(k=1) ^n (((−1)^(k−1) )/(k2^k )) x^k +(x^(n+1) /((n+1)!))θ(x) 2)f(x) =Σ_(n=0) ^∞ ((f^((n)) (0))/(n!)) x^n = f(0) +Σ_(n=1) ^∞ (1/(n!)){(((−1)^(n−1) (n−1)!)/2^n )}x^n =ln(2) + Σ_(n=1) ^∞ (((−1)^(n−1) )/(n 2^n )) x^n .

$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}\left({x}\right)\:=\sum_{{k}=\mathrm{0}} ^{{n}} \frac{{f}^{\left({k}\right)} \left(\mathrm{0}\right)}{{k}!}\:{x}^{{k}} \:\:+\:\frac{{x}^{{n}+\mathrm{1}} }{\left({n}+\mathrm{1}\right)!}\theta\left({x}\right) \\ $$$${with}\:{lim}_{{x}\rightarrow\mathrm{0}} \theta\left({x}\right)=\mathrm{0}\:\:{but} \\ $$$${f}^{'} \left({x}\right)=\:\frac{\mathrm{1}}{{x}+\mathrm{2}}\:\Rightarrow{f}^{\left({k}\right)} \left({x}\right)=\left(\frac{\mathrm{1}}{{x}+\mathrm{2}}\right)^{\left({k}−\mathrm{1}\right)} =\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} \left({k}−\mathrm{1}\right)!}{\left({x}+\mathrm{2}\right)^{{k}} } \\ $$$$\Rightarrow{f}^{\left({k}\right)} \left(\mathrm{0}\right)\:=\:\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} \left({k}−\mathrm{1}\right)!}{{k}!\mathrm{2}^{{k}} }\:{for}\:{k}\geqslant\mathrm{1}\:\Rightarrow \\ $$$${f}\left({x}\right)\:={ln}\left(\mathrm{2}\right)\:+\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} }{{k}\mathrm{2}^{{k}} }\:{x}^{{k}} \:\:+\frac{{x}^{{n}+\mathrm{1}} }{\left({n}+\mathrm{1}\right)!}\theta\left({x}\right) \\ $$$$\left.\mathrm{2}\right){f}\left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{{f}^{\left({n}\right)} \left(\mathrm{0}\right)}{{n}!}\:{x}^{{n}} \\ $$$$=\:{f}\left(\mathrm{0}\right)\:+\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{{n}!}\left\{\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\mathrm{2}^{{n}} }\right\}{x}^{{n}} \\ $$$$={ln}\left(\mathrm{2}\right)\:+\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}\:\mathrm{2}^{{n}} }\:{x}^{{n}} \:. \\ $$$$ \\ $$

Commented by prof Abdo imad last updated on 17/Jul/18

f^((k)) (0)= (((−1)^(k−1) (k−1)!)/2^k ) for k≥1

$${f}^{\left({k}\right)} \left(\mathrm{0}\right)=\:\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} \left({k}−\mathrm{1}\right)!}{\mathrm{2}^{{k}} }\:\:{for}\:{k}\geqslant\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com