Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 4013 by Yozzii last updated on 26/Dec/15

Find x such that (x^2 +5x+5)^(x^2 −21x+10) =1.

$${Find}\:{x}\:{such}\:{that}\:\left({x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{5}\right)^{{x}^{\mathrm{2}} −\mathrm{21}{x}+\mathrm{10}} =\mathrm{1}. \\ $$

Commented by 123456 last updated on 26/Dec/15

x^2 +5x+5=1⇔x^2 +5x+4=0 Δ=5^2 −4(1)(4) Δ=25−16 Δ=9 x=((−5±(√9))/(2(1)))=((−5±3)/2) x_1 =((−5+3)/2)=−1 x_2 =((−5−3)/2)=−4 x^2 −21x+10=0 Δ=(−21)^2 −4(1)(10) Δ=441−40 Δ=401 x=((21±(√(401)))/2)

$${x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{5}=\mathrm{1}\Leftrightarrow{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{4}=\mathrm{0} \\ $$$$\Delta=\mathrm{5}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}\right)\left(\mathrm{4}\right) \\ $$$$\Delta=\mathrm{25}−\mathrm{16} \\ $$$$\Delta=\mathrm{9} \\ $$$${x}=\frac{−\mathrm{5}\pm\sqrt{\mathrm{9}}}{\mathrm{2}\left(\mathrm{1}\right)}=\frac{−\mathrm{5}\pm\mathrm{3}}{\mathrm{2}} \\ $$$${x}_{\mathrm{1}} =\frac{−\mathrm{5}+\mathrm{3}}{\mathrm{2}}=−\mathrm{1} \\ $$$${x}_{\mathrm{2}} =\frac{−\mathrm{5}−\mathrm{3}}{\mathrm{2}}=−\mathrm{4} \\ $$$${x}^{\mathrm{2}} −\mathrm{21}{x}+\mathrm{10}=\mathrm{0} \\ $$$$\Delta=\left(−\mathrm{21}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}\right)\left(\mathrm{10}\right) \\ $$$$\Delta=\mathrm{441}−\mathrm{40} \\ $$$$\Delta=\mathrm{401} \\ $$$${x}=\frac{\mathrm{21}\pm\sqrt{\mathrm{401}}}{\mathrm{2}} \\ $$

Answered by RasheedSindhi last updated on 26/Dec/15

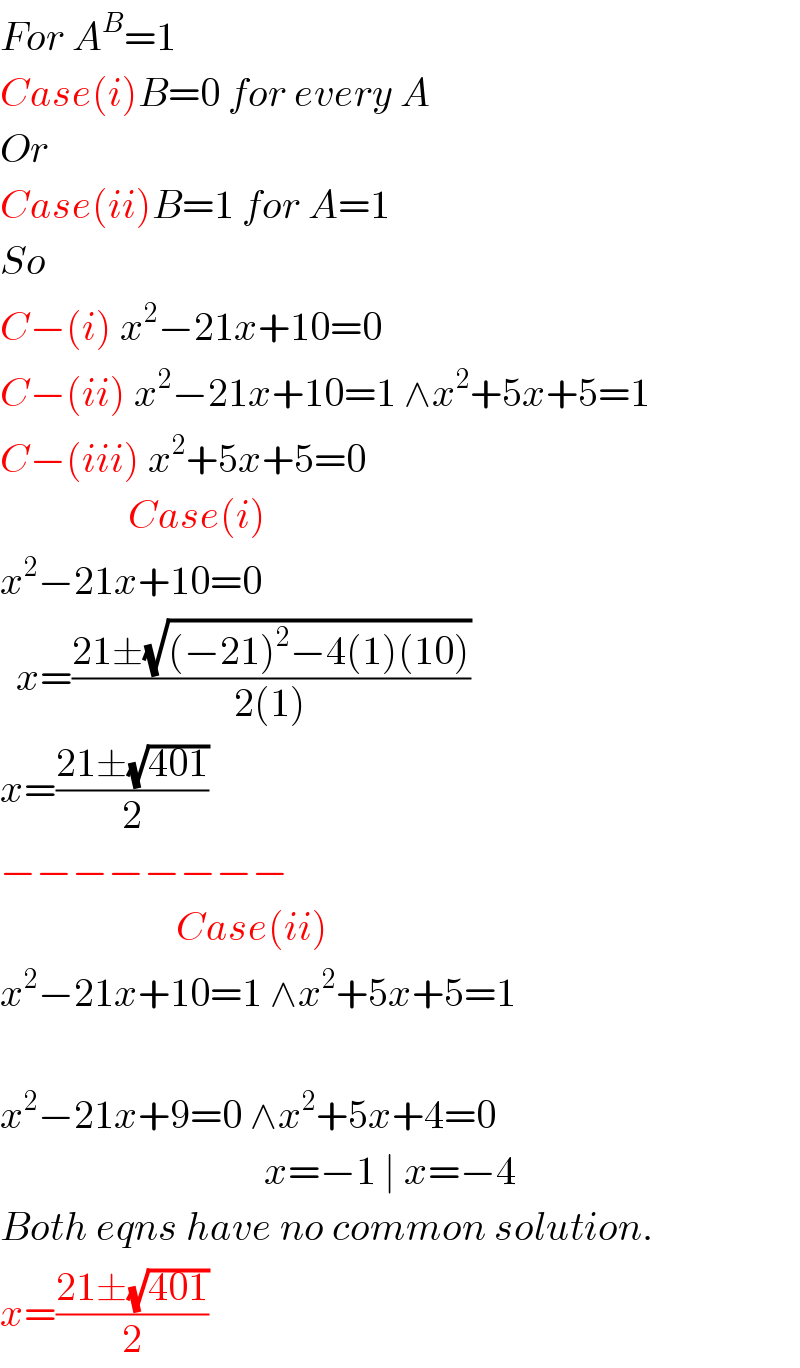
For A^B =1 Case(i)B=0 for every A Or Case(ii)B=1 for A=1 So C−(i) x^2 −21x+10=0 C−(ii) x^2 −21x+10=1 ∧x^2 +5x+5=1 C−(iii) x^2 +5x+5=0 Case(i) x^2 −21x+10=0 x=((21±(√((−21)^2 −4(1)(10))))/(2(1))) x=((21±(√(401)))/2) −−−−−−−− Case(ii) x^2 −21x+10=1 ∧x^2 +5x+5=1 x^2 −21x+9=0 ∧x^2 +5x+4=0 x=−1 ∣ x=−4 Both eqns have no common solution. x=((21±(√(401)))/2)

$${For}\:{A}^{{B}} =\mathrm{1} \\ $$$${Case}\left({i}\right){B}=\mathrm{0}\:{for}\:{every}\:{A} \\ $$$${Or} \\ $$$${Case}\left({ii}\right){B}=\mathrm{1}\:{for}\:{A}=\mathrm{1} \\ $$$${So} \\ $$$${C}−\left({i}\right)\:{x}^{\mathrm{2}} −\mathrm{21}{x}+\mathrm{10}=\mathrm{0} \\ $$$${C}−\left({ii}\right)\:{x}^{\mathrm{2}} −\mathrm{21}{x}+\mathrm{10}=\mathrm{1}\:\wedge{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{5}=\mathrm{1} \\ $$$${C}−\left({iii}\right)\:{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{5}=\mathrm{0}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{Case}\left({i}\right) \\ $$$${x}^{\mathrm{2}} −\mathrm{21}{x}+\mathrm{10}=\mathrm{0} \\ $$$$\:\:{x}=\frac{\mathrm{21}\pm\sqrt{\left(−\mathrm{21}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}\right)\left(\mathrm{10}\right)}}{\mathrm{2}\left(\mathrm{1}\right)} \\ $$$${x}=\frac{\mathrm{21}\pm\sqrt{\mathrm{401}}}{\mathrm{2}} \\ $$$$−−−−−−−− \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{Case}\left({ii}\right) \\ $$$${x}^{\mathrm{2}} −\mathrm{21}{x}+\mathrm{10}=\mathrm{1}\:\wedge{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{5}=\mathrm{1} \\ $$$$ \\ $$$${x}^{\mathrm{2}} −\mathrm{21}{x}+\mathrm{9}=\mathrm{0}\:\wedge{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{4}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}=−\mathrm{1}\:\mid\:{x}=−\mathrm{4} \\ $$$${Both}\:{eqns}\:{have}\:{no}\:{common}\:{solution}. \\ $$$${x}=\frac{\mathrm{21}\pm\sqrt{\mathrm{401}}}{\mathrm{2}} \\ $$

Commented by Yozzii last updated on 26/Dec/15

True. And my question hadn′t specified real x only. Good!

$${True}.\:{And}\:{my}\:{question}\:{hadn}'{t}\:{specified} \\ $$$${real}\:{x}\:{only}.\:{Good}! \\ $$

Commented by Rasheed Soomro last updated on 26/Dec/15

If we consider complex numbers many cases can be considered (however it is not necessary that given equations support all these cases.) For A=ω (Cuberoot of unity) B may be 3k type number. A=i B may be doubly even numbers ETC.

$${If}\:{we}\:{consider}\:{complex}\:{numbers} \\ $$$${many}\:{cases}\:{can}\:{be}\:{considered}\: \\ $$$$\left({however}\:{it}\:{is}\:{not}\:{necessary}\:{that}\right. \\ $$$${given}\:{equations}\:{support}\:{all}\:{these} \\ $$$$\left.{cases}.\right) \\ $$$${For}\:{A}=\omega\:\left({Cuberoot}\:{of}\:{unity}\right)\:{B} \\ $$$${may}\:{be}\:\mathrm{3}{k}\:{type}\:{number}. \\ $$$${A}={i}\:{B}\:{may}\:{be}\:{doubly}\:{even}\:{numbers} \\ $$$${ETC}. \\ $$

Commented by Yozzii last updated on 26/Dec/15

If A=0 and B∈R−{0}, ⇒0^B =0≠1. The third case isn′t required. If you′d like, consider A=−1 and B even. ⇒A^B =(−1)^(2w) =1

$${If}\:{A}=\mathrm{0}\:{and}\:{B}\in\mathbb{R}−\left\{\mathrm{0}\right\},\:\Rightarrow\mathrm{0}^{{B}} =\mathrm{0}\neq\mathrm{1}. \\ $$$${The}\:{third}\:{case}\:{isn}'{t}\:{required}. \\ $$$${If}\:{you}'{d}\:{like},\:{consider}\:{A}=−\mathrm{1}\: \\ $$$${and}\:{B}\:{even}.\:\Rightarrow{A}^{{B}} =\left(−\mathrm{1}\right)^{\mathrm{2}{w}} =\mathrm{1} \\ $$$$ \\ $$

Commented by Yozzii last updated on 26/Dec/15

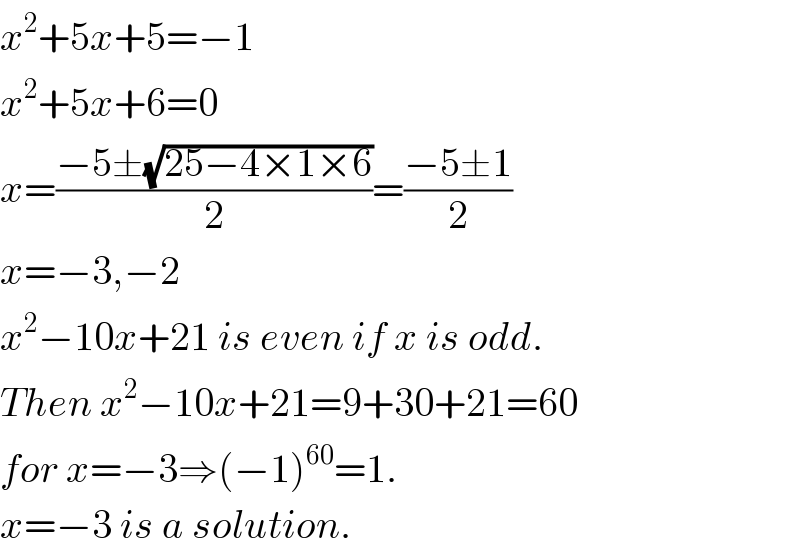
x^2 +5x+5=−1 x^2 +5x+6=0 x=((−5±(√(25−4×1×6)))/2)=((−5±1)/2) x=−3,−2 x^2 −10x+21 is even if x is odd. Then x^2 −10x+21=9+30+21=60 for x=−3⇒(−1)^(60) =1. x=−3 is a solution.

$${x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{5}=−\mathrm{1} \\ $$$${x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{6}=\mathrm{0} \\ $$$${x}=\frac{−\mathrm{5}\pm\sqrt{\mathrm{25}−\mathrm{4}×\mathrm{1}×\mathrm{6}}}{\mathrm{2}}=\frac{−\mathrm{5}\pm\mathrm{1}}{\mathrm{2}} \\ $$$${x}=−\mathrm{3},−\mathrm{2}\: \\ $$$${x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{21}\:{is}\:{even}\:{if}\:{x}\:{is}\:{odd}. \\ $$$${Then}\:{x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{21}=\mathrm{9}+\mathrm{30}+\mathrm{21}=\mathrm{60} \\ $$$${for}\:{x}=−\mathrm{3}\Rightarrow\left(−\mathrm{1}\right)^{\mathrm{60}} =\mathrm{1}. \\ $$$${x}=−\mathrm{3}\:{is}\:{a}\:{solution}. \\ $$

Commented by Yozzii last updated on 26/Dec/15

The case by case approach is ideal and systematic! We just need to ensure all cases are considered...

$${The}\:{case}\:{by}\:{case}\:{approach}\:{is}\:{ideal} \\ $$$${and}\:{systematic}! \\ $$$${We}\:{just}\:{need}\:{to}\:{ensure}\:{all}\:{cases}\:{are} \\ $$$${considered}... \\ $$

Commented by RasheedSindhi last updated on 26/Dec/15

THankS A LoT! YourGuidanceIsAlways Welcomed! 3rd Case is my mistake! I am going to correctit! Actually due to hastiness I have made many mistakes in this answer. A=−1 and B ∈ E is a good suggestion,which was not in my mind!

$$\boldsymbol{\mathcal{T}}\mathcal{H}{ank}\mathcal{S}\:\mathcal{A}\:\mathcal{L}{o}\boldsymbol{\mathcal{T}}! \\ $$$$\boldsymbol{\mathrm{YourGuidanceIsAlways}} \\ $$$$\boldsymbol{\mathrm{Welcomed}}! \\ $$$$\mathrm{3}{rd}\:{Case}\:{is}\:{my}\:{mistake}! \\ $$$${I}\:{am}\:{going}\:{to}\:{correctit}! \\ $$$${Actually}\:{due}\:{to}\:{hastiness} \\ $$$${I}\:{have}\:{made}\:{many}\:{mistakes} \\ $$$${in}\:{this}\:{answer}. \\ $$$${A}=−\mathrm{1}\:{and}\:{B}\:\in\:\mathbb{E}\:{is}\:{a}\:{good} \\ $$$${suggestion},{which}\:{was}\:{not}\:{in} \\ $$$${my}\:{mind}! \\ $$

Answered by Alejandro Prieto last updated on 26/Dec/15

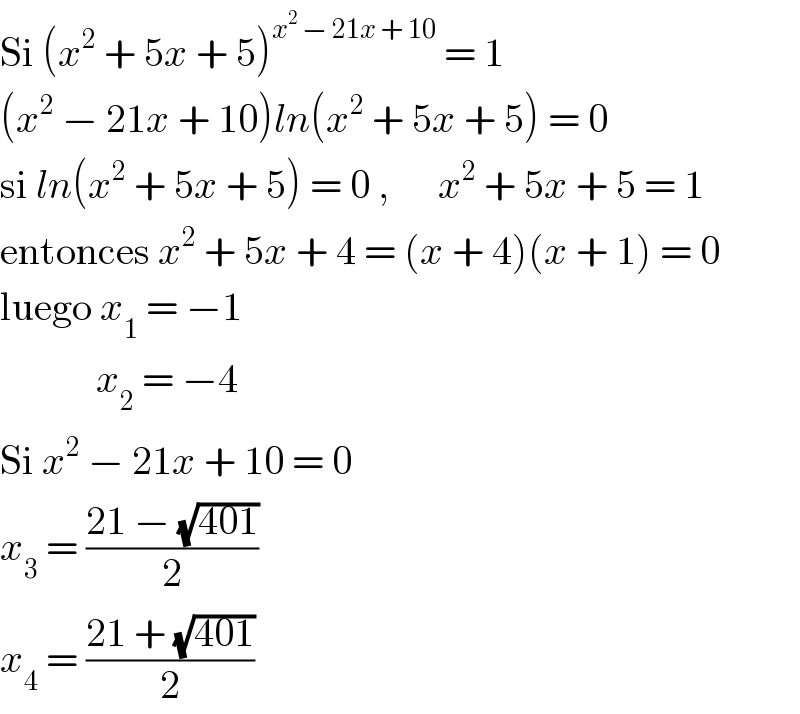
Si (x^2 + 5x + 5)^(x^2 − 21x + 10) = 1 (x^2 − 21x + 10)ln(x^2 + 5x + 5) = 0 si ln(x^2 + 5x + 5) = 0 , x^2 + 5x + 5 = 1 entonces x^2 + 5x + 4 = (x + 4)(x + 1) = 0 luego x_1 = −1 x_2 = −4 Si x^2 − 21x + 10 = 0 x_3 = ((21 − (√(401)))/2) x_4 = ((21 + (√(401)))/2)

$$\mathrm{Si}\:\left({x}^{\mathrm{2}} \:+\:\mathrm{5}{x}\:+\:\mathrm{5}\right)^{{x}^{\mathrm{2}} \:−\:\mathrm{21}{x}\:+\:\mathrm{10}} \:=\:\mathrm{1} \\ $$$$\left({x}^{\mathrm{2}} \:−\:\mathrm{21}{x}\:+\:\mathrm{10}\right){ln}\left({x}^{\mathrm{2}} \:+\:\mathrm{5}{x}\:+\:\mathrm{5}\right)\:=\:\mathrm{0} \\ $$$$\mathrm{si}\:{ln}\left({x}^{\mathrm{2}} \:+\:\mathrm{5}{x}\:+\:\mathrm{5}\right)\:=\:\mathrm{0}\:,\:\:\:\:\:\:{x}^{\mathrm{2}} \:+\:\mathrm{5}{x}\:+\:\mathrm{5}\:=\:\mathrm{1} \\ $$$$\mathrm{entonces}\:{x}^{\mathrm{2}} \:+\:\mathrm{5}{x}\:+\:\mathrm{4}\:=\:\left({x}\:+\:\mathrm{4}\right)\left({x}\:+\:\mathrm{1}\right)\:=\:\mathrm{0} \\ $$$$\mathrm{luego}\:{x}_{\mathrm{1}} \:=\:−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{x}_{\mathrm{2}} \:=\:−\mathrm{4} \\ $$$$\mathrm{Si}\:{x}^{\mathrm{2}} \:−\:\mathrm{21}{x}\:+\:\mathrm{10}\:=\:\mathrm{0} \\ $$$${x}_{\mathrm{3}} \:=\:\frac{\mathrm{21}\:−\:\sqrt{\mathrm{401}}}{\mathrm{2}} \\ $$$${x}_{\mathrm{4}} \:=\:\frac{\mathrm{21}\:+\:\sqrt{\mathrm{401}}}{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com