
Question Number 40138 by maxmathsup by imad last updated on 16/Jul/18
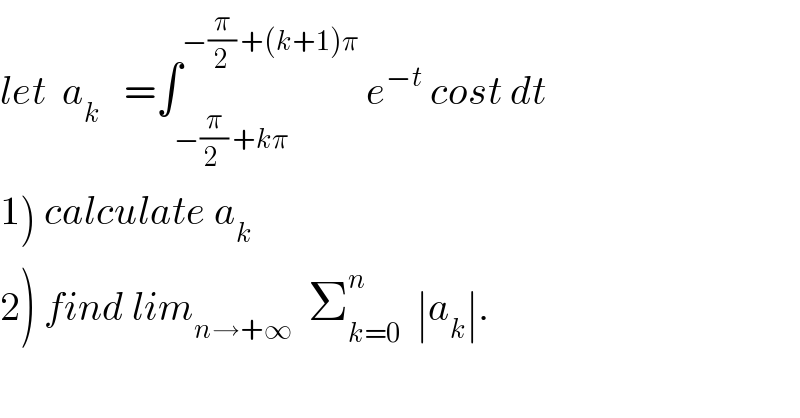
$${let}\:\:{a}_{{k}} \:\:\:=\int_{−\frac{\pi}{\mathrm{2}\:}\:+{k}\pi} ^{−\frac{\pi}{\mathrm{2}}\:+\left({k}+\mathrm{1}\right)\pi} \:{e}^{−{t}} \:{cost}\:{dt} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{a}_{{k}} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{lim}_{{n}\rightarrow+\infty} \:\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\mid{a}_{{k}} \mid. \\ $$
Commented by maxmathsup by imad last updated on 20/Jul/18
![1) we have a_k =_(t=kπ +x) ∫_(−(π/2)) ^(π/2) e^(−(kπ+x)) cos(x+kπ)dx = ∫_(−(π/2)) ^(π/2) e^(−kπ) e^(−x) (−1)^k cosx dx =(−1)^k e^(−kπ) ∫_(−(π/2)) ^(π/2) e^(−x) cosxdx but ∫_(−(π/2)) ^(π/2) e^(−x) cosx dx=Re( ∫_(−(π/2)) ^(π/2) e^(−x) e^(ix) ) =Re( ∫_(−(π/2)) ^(π/2) e^((−1+i)x) dx) =Re( [(1/(−1+i)) e^((−1+i)x) ]_(−(π/2)) ^(π/2) =Re( (1/(−1+i))( e^((−1+i)(π/2)) −e^(−(−1+i)(π/2)) )) =Re{ ((−1)/(1−i))( e^(−(π/2)) i + e^(π/2) i}=Re { ((−i)/(1−i))( e^(π/2) +e^(−(π/2)) )} =Re( ((−i(1+i))/2)( e^(π/2) +e^(−(π/2)) ))= Re( ((−i+1)/2)(e^(π/2) +e^(−(π/2)) )) =((e^(π/2) +e^(−(π/2)) )/2) =ch((π/2)) ⇒ a_k =(−1)^k e^(−kπ) ch((π/2)) .](Q40361.png)
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{a}_{{k}} =_{{t}={k}\pi\:+{x}} \:\:\:\:\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\:{e}^{−\left({k}\pi+{x}\right)} \:{cos}\left({x}+{k}\pi\right){dx} \\ $$$$=\:\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\:{e}^{−{k}\pi} \:{e}^{−{x}} \:\left(−\mathrm{1}\right)^{{k}} {cosx}\:{dx} \\ $$$$=\left(−\mathrm{1}\right)^{{k}} \:{e}^{−{k}\pi} \:\:\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:{e}^{−{x}} \:{cosxdx}\:{but}\:\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:{e}^{−{x}} {cosx}\:{dx}={Re}\left(\:\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:{e}^{−{x}} \:{e}^{{ix}} \right) \\ $$$$={Re}\left(\:\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:{e}^{\left(−\mathrm{1}+{i}\right){x}} {dx}\right)\:={Re}\left(\:\left[\frac{\mathrm{1}}{−\mathrm{1}+{i}}\:{e}^{\left(−\mathrm{1}+{i}\right){x}} \right]_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \right. \\ $$$$={Re}\left(\:\frac{\mathrm{1}}{−\mathrm{1}+{i}}\left(\:{e}^{\left(−\mathrm{1}+{i}\right)\frac{\pi}{\mathrm{2}}} \:−{e}^{−\left(−\mathrm{1}+{i}\right)\frac{\pi}{\mathrm{2}}} \right)\right) \\ $$$$={Re}\left\{\:\:\frac{−\mathrm{1}}{\mathrm{1}−{i}}\left(\:{e}^{−\frac{\pi}{\mathrm{2}}} {i}\:+\:{e}^{\frac{\pi}{\mathrm{2}}} {i}\right\}={Re}\:\left\{\:\frac{−{i}}{\mathrm{1}−{i}}\left(\:{e}^{\frac{\pi}{\mathrm{2}}} \:+{e}^{−\frac{\pi}{\mathrm{2}}} \right)\right\}\right. \\ $$$$={Re}\left(\:\:\frac{−{i}\left(\mathrm{1}+{i}\right)}{\mathrm{2}}\left(\:{e}^{\frac{\pi}{\mathrm{2}}} \:+{e}^{−\frac{\pi}{\mathrm{2}}} \right)\right)=\:{Re}\left(\:\:\frac{−{i}+\mathrm{1}}{\mathrm{2}}\left({e}^{\frac{\pi}{\mathrm{2}}} \:+{e}^{−\frac{\pi}{\mathrm{2}}} \right)\right) \\ $$$$=\frac{{e}^{\frac{\pi}{\mathrm{2}}} \:+{e}^{−\frac{\pi}{\mathrm{2}}} }{\mathrm{2}}\:={ch}\left(\frac{\pi}{\mathrm{2}}\right)\:\Rightarrow \\ $$$${a}_{{k}} =\left(−\mathrm{1}\right)^{{k}} \:{e}^{−{k}\pi} \:{ch}\left(\frac{\pi}{\mathrm{2}}\right)\:. \\ $$
Commented by maxmathsup by imad last updated on 20/Jul/18

$$\left.\mathrm{2}\right)\:{let}\:{S}_{{n}} =\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\mid{a}_{{k}} \mid \\ $$$${S}_{{n}} =\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\:{ch}\left(\frac{\pi}{\mathrm{2}}\right)\:\left({e}^{−\pi} \right)^{{k}} ={ch}\left(\frac{\pi}{\mathrm{2}}\right)\sum_{{k}=\mathrm{0}} ^{{n}} \:\left({e}^{−\pi} \right)^{{k}} \\ $$$$={ch}\left(\frac{\pi}{\mathrm{2}}\right)\:\frac{\mathrm{1}−{e}^{−\left({n}+\mathrm{1}\right)\pi} }{\mathrm{1}−{e}^{−\pi} }\:\Rightarrow\:{lim}_{{n}\rightarrow+\infty} \:\:{S}_{{n}} =\:\frac{{ch}\left(\frac{\pi}{\mathrm{2}}\right)}{\mathrm{1}−{e}^{−\pi} }\:. \\ $$
