Question Number 40140 by maxmathsup by imad last updated on 16/Jul/18
$${calculate}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{sin}\left({x}\right){dx}}{{cos}^{\mathrm{2}} {x}\:+{a}^{\mathrm{2}} \:{sin}^{\mathrm{2}} {x}}{dx} \\ $$
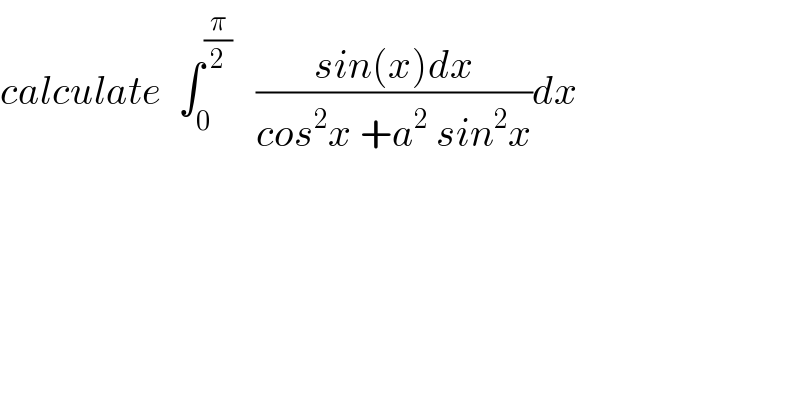
Commented by math khazana by abdo last updated on 20/Jul/18
![let I = ∫_0 ^(π/2) ((sinx)/(cos^2 x +a^2 sin^2 x))dx changement cosx =t give I = −∫_0 ^1 ((−dt)/(t^2 +a^2 (1−t^2 ))) = ∫_0 ^1 (dt/(a^2 +(1−a^2 )t^2 )) = (1/a^2 ) ∫_0 ^1 (dt/(1+((1−a^2 )/a^2 )t^2 )) ( a≠o) case 1 1−a^2 >0 ⇔∣a∣<1 we do the changement (√((1−a^2 )/a^2 )) t =u ⇒ I = (1/a^2 ) ∫_0 ^(√((1−a^2 )/(a^2 ))) (1/(1+u^2 )) (√(a^2 /(1−a^2 ))) du =((∣a∣)/(a^2 (√(1−a^2 )))) ∫_0 ^((√(1−a^2 ))/(∣a∣)) (du/(1+u^2 )) = ((ξ(a))/(a(√(1−a^2 )))) arctan(((√(1−a^2 ))/(∣a∣))) ξ(a)=1 if a>0 and ξ(a)=−1 ifa<0 case 2 1−a^2 <0 ⇒∣a∣>1 ⇒ I = (1/a^2 ) ∫_0 ^1 (dt/(1−((a^2 −1)/a^2 )t^2 )) we do the changement (√((a^2 −1)/a^2 )) t =u ⇒ I = (1/a^2 ) ∫_0 ^((√(a^2 −1))/(∣a∣)) (1/(1−u^2 )) ((∣a∣)/(√(a^2 −1))) du = ((ξ(a))/(√(a^2 −1))) (1/2)∫_0 ^((√(a^2 −1))/(∣a∣)) ((1/(1+u)) +(1/(1−u)))du = ((ξ(a))/(2(√(a^2 −1)))) [ln∣((1+u)/(1−u))∣]_0 ^((√(a^2 −1))/(∣a∣)) =((ξ(a))/(2(√(a^2 −1)))) ln(((1+((√(a^2 −1))/(∣a∣)))/(1−((√(a^2 −1))/(∣a∣))))) =((ξ(a))/(2(√(a^2 −1)))) ln(((∣a∣ +(√(a^2 −1)))/(∣a∣−(√(a^2 −1))))) .](Q40346.png)
$${let}\:{I}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\frac{{sinx}}{{cos}^{\mathrm{2}} {x}\:+{a}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}}{dx}\:{changement} \\ $$$${cosx}\:={t}\:{give}\: \\ $$$${I}\:\:=\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{−{dt}}{{t}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \left(\mathrm{1}−{t}^{\mathrm{2}} \right)} \\ $$$$=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{dt}}{{a}^{\mathrm{2}} \:+\left(\mathrm{1}−{a}^{\mathrm{2}} \right){t}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{dt}}{\mathrm{1}+\frac{\mathrm{1}−{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} }{t}^{\mathrm{2}} } \\ $$$$\left(\:{a}\neq{o}\right) \\ $$$${case}\:\mathrm{1}\:\:\mathrm{1}−{a}^{\mathrm{2}} >\mathrm{0}\:\Leftrightarrow\mid{a}\mid<\mathrm{1}\:\:{we}\:{do}\:{the}\:{changement} \\ $$$$\sqrt{\frac{\mathrm{1}−{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} }}\:{t}\:={u}\:\Rightarrow \\ $$$${I}\:\:=\:\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\:\:\int_{\mathrm{0}} ^{\sqrt{\frac{\mathrm{1}−{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} \:}}} \:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }\:\sqrt{\frac{{a}^{\mathrm{2}} }{\mathrm{1}−{a}^{\mathrm{2}} }}\:{du} \\ $$$$=\frac{\mid{a}\mid}{{a}^{\mathrm{2}} \:\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}\:\:\int_{\mathrm{0}} ^{\frac{\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}{\mid{a}\mid}} \:\:\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\:\frac{\xi\left({a}\right)}{{a}\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}\:{arctan}\left(\frac{\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}{\mid{a}\mid}\right)\: \\ $$$$\xi\left({a}\right)=\mathrm{1}\:{if}\:{a}>\mathrm{0}\:{and}\:\xi\left({a}\right)=−\mathrm{1}\:{ifa}<\mathrm{0} \\ $$$${case}\:\mathrm{2}\:\:\mathrm{1}−{a}^{\mathrm{2}} <\mathrm{0}\:\Rightarrow\mid{a}\mid>\mathrm{1}\:\Rightarrow \\ $$$${I}\:=\:\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\:\frac{{dt}}{\mathrm{1}−\frac{{a}^{\mathrm{2}} −\mathrm{1}}{{a}^{\mathrm{2}} }{t}^{\mathrm{2}} }\:{we}\:{do}\:{the}\:{changement} \\ $$$$\sqrt{\frac{{a}^{\mathrm{2}} \:−\mathrm{1}}{{a}^{\mathrm{2}} }}\:{t}\:={u}\:\Rightarrow \\ $$$${I}\:=\:\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\frac{\sqrt{{a}^{\mathrm{2}} \:−\mathrm{1}}}{\mid{a}\mid}} \:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}−{u}^{\mathrm{2}} }\:\:\frac{\mid{a}\mid}{\sqrt{{a}^{\mathrm{2}} \:−\mathrm{1}}}\:{du} \\ $$$$=\:\frac{\xi\left({a}\right)}{\sqrt{{a}^{\mathrm{2}} \:−\mathrm{1}}}\:\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\sqrt{{a}^{\mathrm{2}} \:−\mathrm{1}}}{\mid{a}\mid}} \:\:\:\left(\frac{\mathrm{1}}{\mathrm{1}+{u}}\:+\frac{\mathrm{1}}{\mathrm{1}−{u}}\right){du} \\ $$$$=\:\frac{\xi\left({a}\right)}{\mathrm{2}\sqrt{{a}^{\mathrm{2}} \:−\mathrm{1}}}\:\left[{ln}\mid\frac{\mathrm{1}+{u}}{\mathrm{1}−{u}}\mid\right]_{\mathrm{0}} ^{\frac{\sqrt{{a}^{\mathrm{2}} \:−\mathrm{1}}}{\mid{a}\mid}} \\ $$$$=\frac{\xi\left({a}\right)}{\mathrm{2}\sqrt{{a}^{\mathrm{2}} \:−\mathrm{1}}}\:{ln}\left(\frac{\mathrm{1}+\frac{\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}}{\mid{a}\mid}}{\mathrm{1}−\frac{\sqrt{{a}^{\mathrm{2}} \:−\mathrm{1}}}{\mid{a}\mid}}\right) \\ $$$$=\frac{\xi\left({a}\right)}{\mathrm{2}\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}}\:{ln}\left(\frac{\mid{a}\mid\:+\sqrt{{a}^{\mathrm{2}} \:−\mathrm{1}}}{\mid{a}\mid−\sqrt{{a}^{\mathrm{2}} \:−\mathrm{1}}}\right)\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 18/Jul/18
$${t}={cosx}\:\:{dt}=−{sinx}\:{dx} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{0}} \frac{−{dt}}{{t}^{\mathrm{2}} +{a}^{\mathrm{2}} \left(\mathrm{1}−{t}^{\mathrm{2}} \right)} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{{a}^{\mathrm{2}} +{t}^{\mathrm{2}} \left(\mathrm{1}−{a}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−{a}^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{\frac{{a}^{\mathrm{2}} }{\mathrm{1}−{a}^{\mathrm{2}} }+{t}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−{a}^{\mathrm{2}} }×\frac{\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }\:}{{a}}\mid{tan}^{−\mathrm{1}} \left(\frac{{t}}{\sqrt{\frac{{a}^{\mathrm{2}} }{\mathrm{1}−{a}^{\mathrm{2}} }}}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }\:}{\left({a}−{a}^{\mathrm{3}} \right)}\mid{tan}^{−\mathrm{1}} \left(\frac{{t}\sqrt{\mathrm{1}−{a}^{\mathrm{2}} \:}}{{a}}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}{{a}−{a}^{\mathrm{3}} }{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}{{a}}\right) \\ $$$$ \\ $$
Commented by math khazana by abdo last updated on 20/Jul/18
$${sir}\:{Tanmay}\:\:{you}\:{must}\:{studythe}\:{cases}\:\mid{a}\mid>\mathrm{1} \\ $$$${and}\:\mid{a}\mid<\mathrm{1}\:.... \\ $$