
Question and Answers Forum
Question Number 40159 by maxmathsup by imad last updated on 16/Jul/18
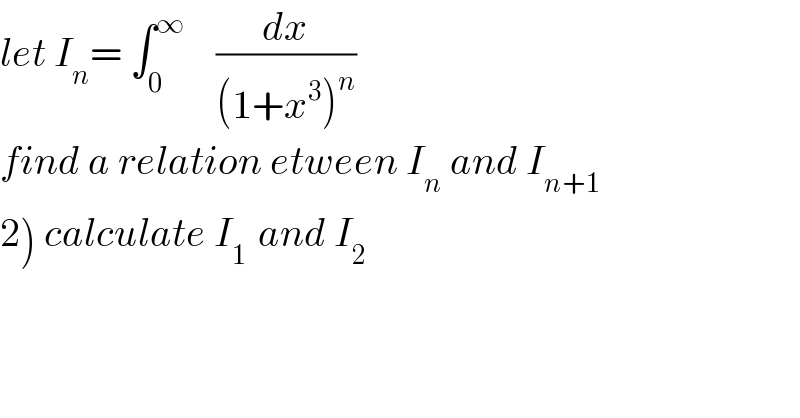
Commented by prof Abdo imad last updated on 17/Jul/18
![1) we have I_n = ∫_0 ^∞ ((1+x^3 )/((1+x^3 )^(n+1) ))dx =I_(n+1) + ∫_0 ^∞ (x^3 /((1+x^3 )^(n+1) ))dx by parts ∫_0 ^∞ (x^3 /((1+x^3 )^3 ))dx =(1/3)∫_0 ^∞ x(((3x^2 )/((1+x^3 )^(n+1) )))dx =(1/3)∫_0 ^∞ x ( 3x^2 (1+x^3 )^(−n−1) )dx =(1/3)[−(x/n)(1+x^3 )^(−n) ]_0 ^(+∞) −(1/3)∫_0 ^∞ 1 (−(1/n))(1/((1+x^3 )^n ))dx = (1/(3n)) I_n ⇒ I_n = I_(n+1) +(1/(3n)) I_n ⇒ (1−(1/(3n))) I_n = I_(n+1) ⇒ I_(n+1) =((3n−1)/(3n)) I_n 2) we have I_1 = ∫_0 ^∞ (dx/(1+x^3 )) =_(x^ =t^(1/3) ) ∫_0 ^∞ (1/(1+t)) (1/3)t^((1/3)−1) dt =(1/3) ∫_0 ^∞ (t^((1/3)−1) /(1+t))dt =(1/3) (π/(sin((π/3)))) =(π/(3.((√3)/2))) = ((2π)/(3(√3))) I_2 = (2/3) I_1 = (2/3) ((2π)/(3(√3))) = ((4π)/(9(√3))) .](Q40219.png)
| ||
Question and Answers Forum | ||
Question Number 40159 by maxmathsup by imad last updated on 16/Jul/18 | ||
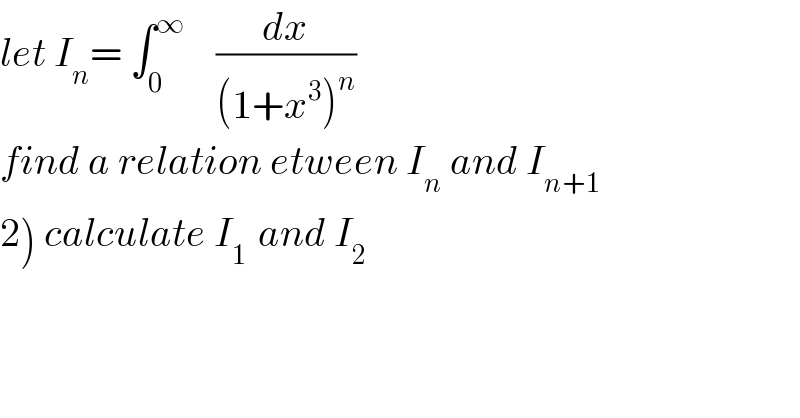 | ||
Commented by prof Abdo imad last updated on 17/Jul/18 | ||
![1) we have I_n = ∫_0 ^∞ ((1+x^3 )/((1+x^3 )^(n+1) ))dx =I_(n+1) + ∫_0 ^∞ (x^3 /((1+x^3 )^(n+1) ))dx by parts ∫_0 ^∞ (x^3 /((1+x^3 )^3 ))dx =(1/3)∫_0 ^∞ x(((3x^2 )/((1+x^3 )^(n+1) )))dx =(1/3)∫_0 ^∞ x ( 3x^2 (1+x^3 )^(−n−1) )dx =(1/3)[−(x/n)(1+x^3 )^(−n) ]_0 ^(+∞) −(1/3)∫_0 ^∞ 1 (−(1/n))(1/((1+x^3 )^n ))dx = (1/(3n)) I_n ⇒ I_n = I_(n+1) +(1/(3n)) I_n ⇒ (1−(1/(3n))) I_n = I_(n+1) ⇒ I_(n+1) =((3n−1)/(3n)) I_n 2) we have I_1 = ∫_0 ^∞ (dx/(1+x^3 )) =_(x^ =t^(1/3) ) ∫_0 ^∞ (1/(1+t)) (1/3)t^((1/3)−1) dt =(1/3) ∫_0 ^∞ (t^((1/3)−1) /(1+t))dt =(1/3) (π/(sin((π/3)))) =(π/(3.((√3)/2))) = ((2π)/(3(√3))) I_2 = (2/3) I_1 = (2/3) ((2π)/(3(√3))) = ((4π)/(9(√3))) .](Q40219.png) | ||