Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 40260 by maxmathsup by imad last updated on 17/Jul/18

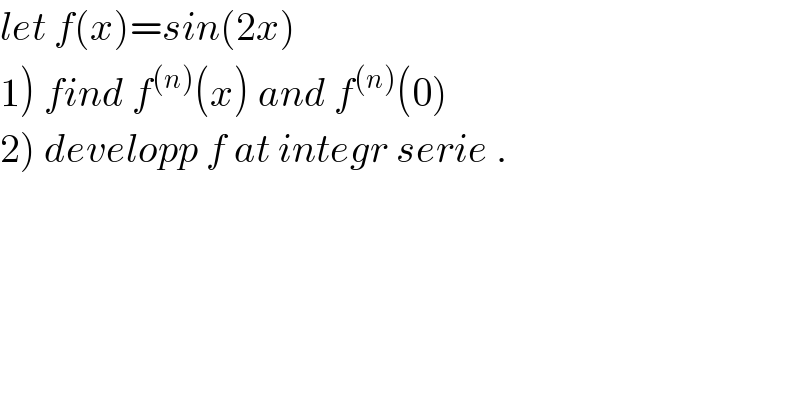
let f(x)=sin(2x) 1) find f^((n)) (x) and f^((n)) (0) 2) developp f at integr serie .

$${let}\:{f}\left({x}\right)={sin}\left(\mathrm{2}{x}\right) \\ $$$$\left.\mathrm{1}\right)\:{find}\:{f}^{\left({n}\right)} \left({x}\right)\:{and}\:{f}^{\left({n}\right)} \left(\mathrm{0}\right) \\ $$$$\left.\mathrm{2}\right)\:{developp}\:{f}\:{at}\:{integr}\:{serie}\:. \\ $$

Commented by maxmathsup by imad last updated on 18/Jul/18

1) we have f(x)=2sin(x)cos(x) ⇒f^((n)) (x)=2Σ_(k=0) ^n C_n ^k (sinx)^((k)) (cosx)^((n−k)) =2Σ_(k=0) ^n C_n ^k sin(x+((kπ)/2))cos(x +(((n−k)π)/2)) ⇒ f^((n)) (0) = 2 Σ_(k=0) ^n C_n ^k sin(((kπ)/2))cos((((n−k)π)/2)) =2 Σ_(p=0) ^([((n−1)/2)]) C_n ^(2p+1) sin((((2p+1)π)/2))cos((((n−2p−1)π)/2)) =2Σ_(p=0) ^([((n−1)/2)]) (−1)^p C_n ^(2p+1) cos( (((n−1)π)/2) −pπ) = 2 Σ_(p=0) ^([((n−1)/2)]) C_n ^(2p+1) cos((((n−1)π)/2)) 2) f(x) = Σ_(n=0) ^∞ ((f^((n)) (0))/(n!)) x^n =Σ_(n=1) ^∞ ((f^((n)) (0))/(n!)) x^n f(x)= Σ_(n=1) ^∞ (2/(n!)) cos((((n−1)π)/2)) (Σ_(p=0) ^([((n−1)/2)]) C_n ^(2p+1) ) x^n

$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}\left({x}\right)=\mathrm{2}{sin}\left({x}\right){cos}\left({x}\right)\:\Rightarrow{f}^{\left({n}\right)} \left({x}\right)=\mathrm{2}\sum_{{k}=\mathrm{0}} ^{{n}} \:\:{C}_{{n}} ^{{k}} \:\:\left({sinx}\right)^{\left({k}\right)} \left({cosx}\right)^{\left({n}−{k}\right)} \\ $$$$=\mathrm{2}\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\:{C}_{{n}} ^{{k}} \:\:{sin}\left({x}+\frac{{k}\pi}{\mathrm{2}}\right){cos}\left({x}\:+\frac{\left({n}−{k}\right)\pi}{\mathrm{2}}\right)\:\Rightarrow \\ $$$${f}^{\left({n}\right)} \left(\mathrm{0}\right)\:=\:\mathrm{2}\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\:{C}_{{n}} ^{{k}} \:{sin}\left(\frac{{k}\pi}{\mathrm{2}}\right){cos}\left(\frac{\left({n}−{k}\right)\pi}{\mathrm{2}}\right) \\ $$$$=\mathrm{2}\:\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:\:\:{C}_{{n}} ^{\mathrm{2}{p}+\mathrm{1}} \:\:{sin}\left(\frac{\left(\mathrm{2}{p}+\mathrm{1}\right)\pi}{\mathrm{2}}\right){cos}\left(\frac{\left({n}−\mathrm{2}{p}−\mathrm{1}\right)\pi}{\mathrm{2}}\right) \\ $$$$=\mathrm{2}\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:\left(−\mathrm{1}\right)^{{p}} \:{C}_{{n}} ^{\mathrm{2}{p}+\mathrm{1}} \:{cos}\left(\:\frac{\left({n}−\mathrm{1}\right)\pi}{\mathrm{2}}\:−{p}\pi\right) \\ $$$$\:=\:\mathrm{2}\:\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:\:{C}_{{n}} ^{\mathrm{2}{p}+\mathrm{1}} \:{cos}\left(\frac{\left({n}−\mathrm{1}\right)\pi}{\mathrm{2}}\right) \\ $$$$\left.\mathrm{2}\right)\:{f}\left({x}\right)\:=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{{f}^{\left({n}\right)} \left(\mathrm{0}\right)}{{n}!}\:{x}^{{n}} \:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{f}^{\left({n}\right)} \left(\mathrm{0}\right)}{{n}!}\:{x}^{{n}} \\ $$$${f}\left({x}\right)=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\mathrm{2}}{{n}!}\:{cos}\left(\frac{\left({n}−\mathrm{1}\right)\pi}{\mathrm{2}}\right)\:\left(\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:\:{C}_{{n}} ^{\mathrm{2}{p}+\mathrm{1}} \right)\:{x}^{{n}} \\ $$$$ \\ $$$$ \\ $$

Commented by maxmathsup by imad last updated on 18/Jul/18

2) another method we have sint =Im( e^(it) )=Im( Σ_(n=0) ^∞ (((it)^n )/(n!))) = Im( Σ_(n=0) ^∞ (((−1)^n t^(2n) )/((2n)!)) +iΣ_(n=0) ^∞ (((−1)^n t^(2n+1) )/((2n+1)!))) =Σ_(n=0) ^∞ (((−1)^n t^(2n+1) )/((2n+1)!)) ⇒ sin(2x) =Σ_(n=0) ^∞ (((−1)^n 2^(2n+1) x^(2n+1) )/((2n+1)!)) and the radius of convergence is R=+∞

$$\left.\mathrm{2}\right)\:{another}\:{method}\:\:{we}\:{have}\:{sint}\:={Im}\left(\:{e}^{{it}} \right)={Im}\left(\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left({it}\right)^{{n}} }{{n}!}\right) \\ $$$$=\:{Im}\left(\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} \:{t}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!}\:+{i}\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} \:{t}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} \:{t}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}\:\:\Rightarrow \\ $$$${sin}\left(\mathrm{2}{x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} \:\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} \:{x}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}\:\:{and}\:{the}\:{radius}\:{of}\:{convergence}\:{is}\:{R}=+\infty \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com