
Question and Answers Forum
Question Number 40352 by scientist last updated on 20/Jul/18
![If A= [((4 −3)),((1 0)) ]use the fact that A^2 =4A−3I_2 and mathematical induction to prove A^n =(((3^n −1))/2)A +((3−3^n )/2)I if n≥1](Q40352.png)
Commented by prof Abdo imad last updated on 20/Jul/18
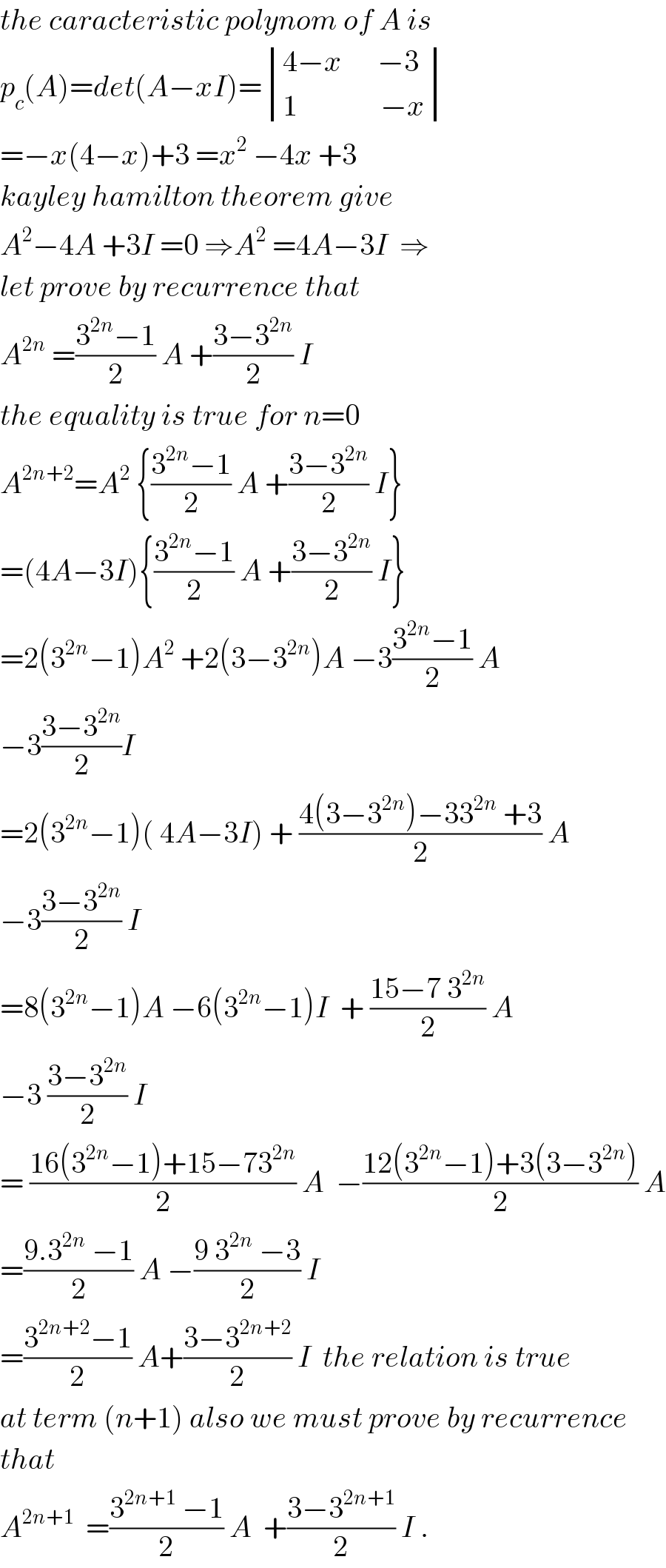
| ||
Question and Answers Forum | ||
Question Number 40352 by scientist last updated on 20/Jul/18 | ||
![If A= [((4 −3)),((1 0)) ]use the fact that A^2 =4A−3I_2 and mathematical induction to prove A^n =(((3^n −1))/2)A +((3−3^n )/2)I if n≥1](Q40352.png) | ||
Commented by prof Abdo imad last updated on 20/Jul/18 | ||
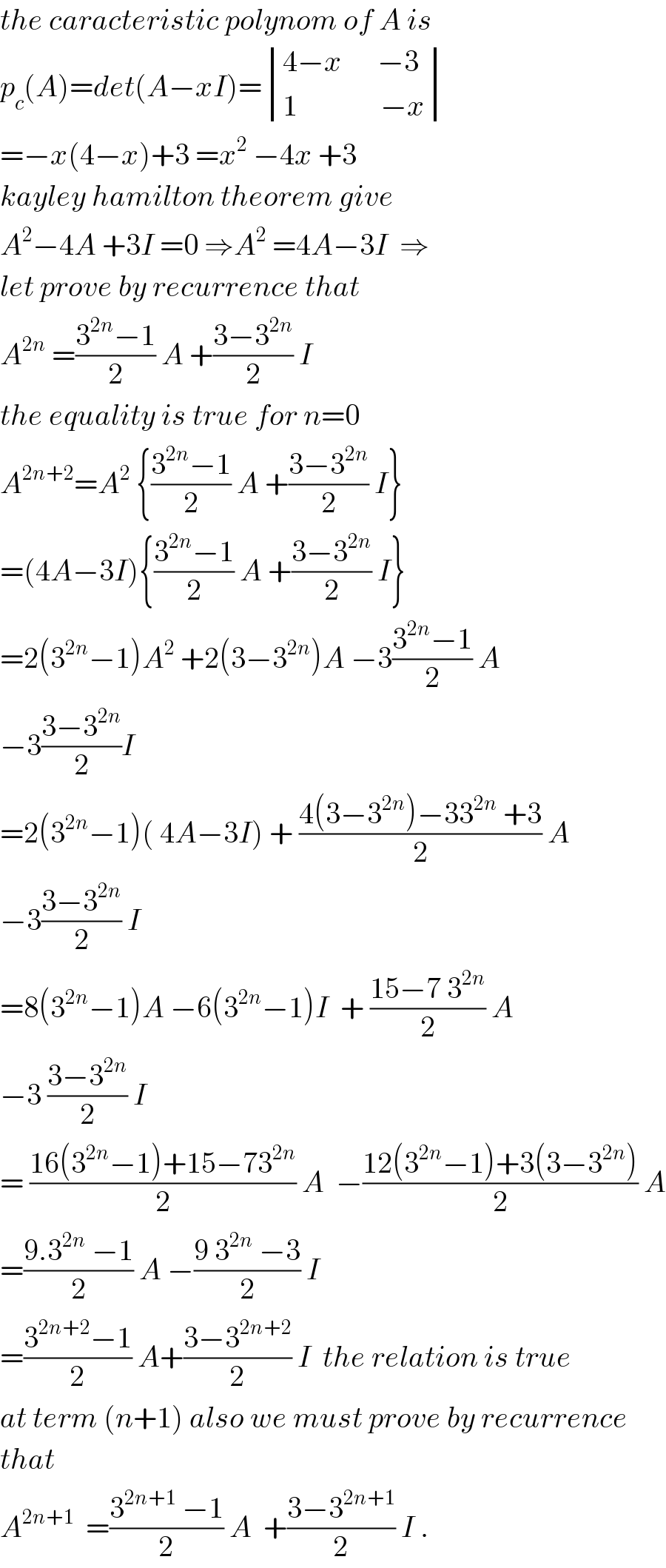 | ||