Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 4040 by Filup last updated on 27/Dec/15

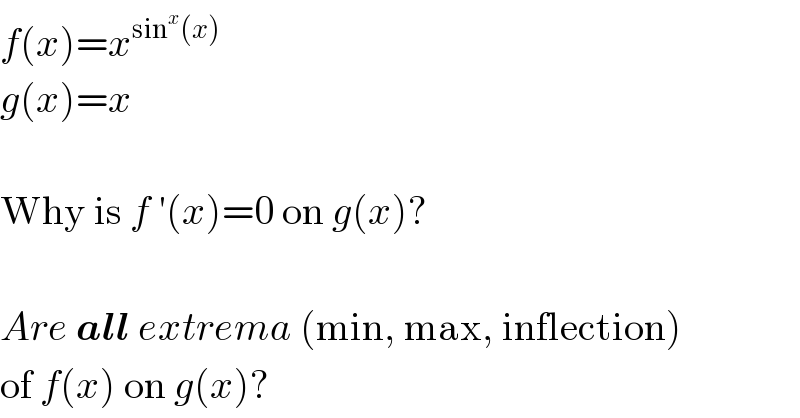
f(x)=x^(sin^x (x)) g(x)=x Why is f ′(x)=0 on g(x)? Are all extrema (min, max, inflection) of f(x) on g(x)?

$${f}\left({x}\right)={x}^{\mathrm{sin}^{{x}} \left({x}\right)} \\ $$$${g}\left({x}\right)={x} \\ $$$$ \\ $$$$\mathrm{Why}\:\mathrm{is}\:{f}\:'\left({x}\right)=\mathrm{0}\:\mathrm{on}\:{g}\left({x}\right)? \\ $$$$ \\ $$$${Are}\:\boldsymbol{{all}}\:{extrema}\:\left(\mathrm{min},\:\mathrm{max},\:\mathrm{inflection}\right) \\ $$$$\mathrm{of}\:{f}\left({x}\right)\:\mathrm{on}\:{g}\left({x}\right)? \\ $$

Commented by Filup last updated on 27/Dec/15

Commented by Filup last updated on 27/Dec/15

So, when does: (df/dx)=g

$$\mathrm{So},\:\mathrm{when}\:\mathrm{does}: \\ $$$$\frac{{df}}{{dx}}={g} \\ $$

Commented by Yozzii last updated on 27/Dec/15

f(x)=x^(sin^x x) (∗) If f(x),x>0, taking ln on both sides of (∗) ⇒lnf(x)=(sin^x x)lnx (∗∗) Again, if lnf(x),(sin^x x)lnx>0, taking ln on both sidds of (∗∗) ⇒ln(lnf(x))=ln{(sin^x x)lnx} ln(lnf(x))=xlnsinx+ln(lnx) (∗∗∗) Implicitly differentiating (∗∗∗) w.r.t x gives (((d/dx)(lnf(x)))/(lnf(x)))=1×lnsinx+x×((cosx)/(sinx))+(((d/dx)(lnx))/(lnx)) (((1/(f(x)))f^( ′) (x))/(lnf(x)))=lnsinx+xcotx+((1/x)/(lnx)) ((f^( ′) (x))/(f(x)lnf(x)))=lnsinx+xcotx+(1/(xlnx)) f^( ′) (x)=f(x)lnf(x){lnsinx+xcotx+(1/(xlnx))} f^′ (x)=x^(sin^x x) lnx^(sin^x x) (1/(xlnx))(xlnx{lnsinx+xcotx}+1) f^′ (x)=((x^(sin^x x) (sin^x x)lnx(x(lnx){lnsinx+xcotx}+1))/(xlnx)) x,lnx>0 ∴f^′ (x)=x^(sin^x x−1) (sin^x x)(x(lnx){lnsinx+xcotx}+1) If f^′ (x)=0 ⇒sin^x x=0⇒x=nπ,x∈N f(nπ)=(nπ)^((sin{nπ})^(nπ) ) =(nπ)^0 =1 If g(x)=x touches f(x)=x^(sin^x x) it is necessary that ∃x∈R∣f^′ (x)=g^′ (x)=1.

$${f}\left({x}\right)={x}^{{sin}^{{x}} {x}} \:\:\:\:\:\:\left(\ast\right) \\ $$$${If}\:{f}\left({x}\right),{x}>\mathrm{0},\:{taking}\:{ln}\:{on}\:{both}\:{sides}\:{of}\:\left(\ast\right) \\ $$$$\Rightarrow{lnf}\left({x}\right)=\left({sin}^{{x}} {x}\right){lnx}\:\:\:\left(\ast\ast\right) \\ $$$${Again},\:{if}\:{lnf}\left({x}\right),\left({sin}^{{x}} {x}\right){lnx}>\mathrm{0},\: \\ $$$${taking}\:{ln}\:{on}\:{both}\:{sidds}\:{of}\:\left(\ast\ast\right) \\ $$$$\Rightarrow{ln}\left({lnf}\left({x}\right)\right)={ln}\left\{\left({sin}^{{x}} {x}\right){lnx}\right\} \\ $$$${ln}\left({lnf}\left({x}\right)\right)={xlnsinx}+{ln}\left({lnx}\right)\:\:\left(\ast\ast\ast\right) \\ $$$${Implicitly}\:{differentiating}\:\:\left(\ast\ast\ast\right)\:{w}.{r}.{t}\:{x} \\ $$$${gives}\: \\ $$$$\frac{\frac{{d}}{{dx}}\left({lnf}\left({x}\right)\right)}{{lnf}\left({x}\right)}=\mathrm{1}×{lnsinx}+{x}×\frac{{cosx}}{{sinx}}+\frac{\frac{{d}}{{dx}}\left({lnx}\right)}{{lnx}} \\ $$$$\frac{\frac{\mathrm{1}}{{f}\left({x}\right)}{f}^{\:'} \left({x}\right)}{{lnf}\left({x}\right)}={lnsinx}+{xcotx}+\frac{\mathrm{1}/{x}}{{lnx}} \\ $$$$\frac{{f}^{\:'} \left({x}\right)}{{f}\left({x}\right){lnf}\left({x}\right)}={lnsinx}+{xcotx}+\frac{\mathrm{1}}{{xlnx}} \\ $$$${f}^{\:'} \left({x}\right)={f}\left({x}\right){lnf}\left({x}\right)\left\{{lnsinx}+{xcotx}+\frac{\mathrm{1}}{{xlnx}}\right\} \\ $$$${f}^{'} \left({x}\right)={x}^{{sin}^{{x}} {x}} {lnx}^{{sin}^{{x}} {x}} \frac{\mathrm{1}}{{xlnx}}\left({xlnx}\left\{{lnsinx}+{xcotx}\right\}+\mathrm{1}\right) \\ $$$${f}^{'} \left({x}\right)=\frac{{x}^{{sin}^{{x}} {x}} \left({sin}^{{x}} {x}\right){lnx}\left({x}\left({lnx}\right)\left\{{lnsinx}+{xcotx}\right\}+\mathrm{1}\right)}{{xlnx}} \\ $$$${x},{lnx}>\mathrm{0} \\ $$$$\therefore{f}^{'} \left({x}\right)={x}^{{sin}^{{x}} {x}−\mathrm{1}} \left({sin}^{{x}} {x}\right)\left({x}\left({lnx}\right)\left\{{lnsinx}+{xcotx}\right\}+\mathrm{1}\right) \\ $$$${If}\:{f}^{'} \left({x}\right)=\mathrm{0}\: \\ $$$$\Rightarrow{sin}^{{x}} {x}=\mathrm{0}\Rightarrow{x}={n}\pi,{x}\in\mathbb{N} \\ $$$${f}\left({n}\pi\right)=\left({n}\pi\right)^{\left({sin}\left\{{n}\pi\right\}\right)^{{n}\pi} } =\left({n}\pi\right)^{\mathrm{0}} =\mathrm{1} \\ $$$$ \\ $$$${If}\:{g}\left({x}\right)={x}\:{touches}\:{f}\left({x}\right)={x}^{{sin}^{{x}} {x}} \\ $$$${it}\:{is}\:{necessary}\:{that}\:\exists{x}\in\mathbb{R}\mid{f}^{'} \left({x}\right)={g}^{'} \left({x}\right)=\mathrm{1}. \\ $$$$ \\ $$

Commented by Yozzii last updated on 27/Dec/15

Commented by Yozzii last updated on 27/Dec/15

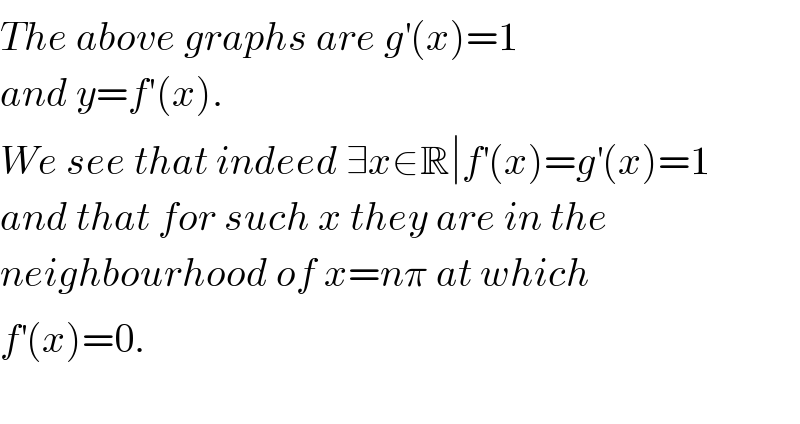
The above graphs are g^′ (x)=1 and y=f′(x). We see that indeed ∃x∈R∣f^′ (x)=g^′ (x)=1 and that for such x they are in the neighbourhood of x=nπ at which f^′ (x)=0.

$${The}\:{above}\:{graphs}\:{are}\:{g}^{'} \left({x}\right)=\mathrm{1} \\ $$$${and}\:{y}={f}'\left({x}\right). \\ $$$${We}\:{see}\:{that}\:{indeed}\:\exists{x}\in\mathbb{R}\mid{f}^{'} \left({x}\right)={g}^{'} \left({x}\right)=\mathrm{1} \\ $$$${and}\:{that}\:{for}\:{such}\:{x}\:{they}\:{are}\:{in}\:{the}\: \\ $$$${neighbourhood}\:{of}\:{x}={n}\pi\:{at}\:{which}\: \\ $$$${f}^{'} \left({x}\right)=\mathrm{0}.\: \\ $$$$ \\ $$

Commented by Yozzii last updated on 27/Dec/15

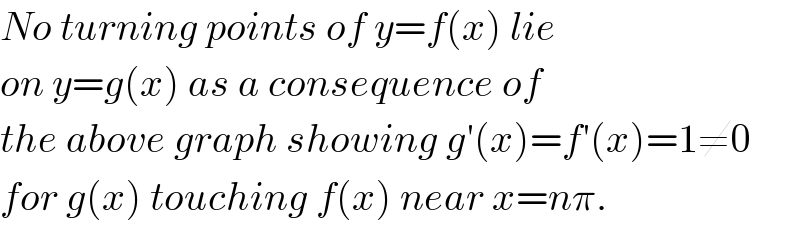
No turning points of y=f(x) lie on y=g(x) as a consequence of the above graph showing g′(x)=f′(x)=1≠0 for g(x) touching f(x) near x=nπ.

$${No}\:{turning}\:{points}\:{of}\:{y}={f}\left({x}\right)\:{lie}\: \\ $$$${on}\:{y}={g}\left({x}\right)\:{as}\:{a}\:{consequence}\:{of}\: \\ $$$${the}\:{above}\:{graph}\:{showing}\:{g}'\left({x}\right)={f}'\left({x}\right)=\mathrm{1}\neq\mathrm{0} \\ $$$${for}\:{g}\left({x}\right)\:{touching}\:{f}\left({x}\right)\:{near}\:{x}={n}\pi. \\ $$

Commented by Filup last updated on 27/Dec/15

This is amazing and complicated! I don′t know implicite differentiation, but this is awesome!!!

$$\mathrm{This}\:\mathrm{is}\:\mathrm{amazing}\:\mathrm{and}\:\mathrm{complicated}! \\ $$$$\mathrm{I}\:\mathrm{don}'{t}\:\mathrm{know}\:\mathrm{implicite}\:\mathrm{differentiation}, \\ $$$$\mathrm{but}\:\mathrm{this}\:\mathrm{is}\:\mathrm{awesome}!!! \\ $$

Commented by Yozzii last updated on 27/Dec/15

This is why I′m glad we can use diagrams now. Graphing is important.

$${This}\:{is}\:{why}\:{I}'{m}\:{glad}\:{we}\:{can}\:{use} \\ $$$${diagrams}\:{now}.\:{Graphing}\:{is}\:{important}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com