
Question and Answers Forum
Question Number 40625 by Raj Singh last updated on 25/Jul/18

Answered by MJS last updated on 25/Jul/18
![∫(dx/((√x)+(x)^(1/3) ))= [t=(x)^(1/6) → dx=6(x^5 )^(1/6) dt] =6∫(t^3 /(t+1))dt=6∫(t^2 −t+1−(1/(t+1)))dt= =6((1/3)t^3 −(1/2)t^2 +t−ln (t+1))= =2t^3 −3t^2 +6t−6ln (t+1)= =2(√x)−3(x)^(1/3) +6(x)^(1/6) −6ln (1+(x)^(1/6) ) +C](Q40627.png)
Commented by MJS last updated on 25/Jul/18
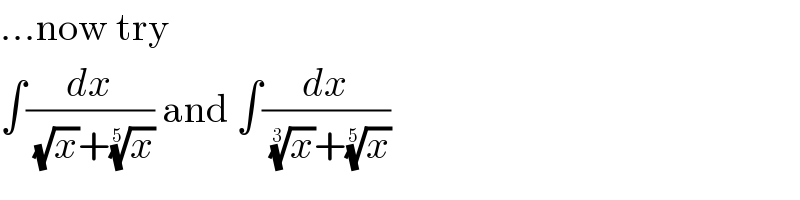
Answered by Joel578 last updated on 25/Jul/18

| ||
Question and Answers Forum | ||
Question Number 40625 by Raj Singh last updated on 25/Jul/18 | ||
 | ||
Answered by MJS last updated on 25/Jul/18 | ||
![∫(dx/((√x)+(x)^(1/3) ))= [t=(x)^(1/6) → dx=6(x^5 )^(1/6) dt] =6∫(t^3 /(t+1))dt=6∫(t^2 −t+1−(1/(t+1)))dt= =6((1/3)t^3 −(1/2)t^2 +t−ln (t+1))= =2t^3 −3t^2 +6t−6ln (t+1)= =2(√x)−3(x)^(1/3) +6(x)^(1/6) −6ln (1+(x)^(1/6) ) +C](Q40627.png) | ||
| ||
Commented by MJS last updated on 25/Jul/18 | ||
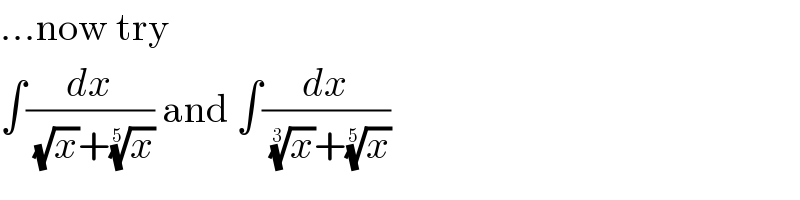 | ||
Answered by Joel578 last updated on 25/Jul/18 | ||
 | ||
| ||