
Question and Answers Forum
Question Number 40637 by Tawa1 last updated on 25/Jul/18

Answered by MJS last updated on 25/Jul/18
![l_1 : y=(x/3)+(a/3) l_2 : y=2x l_3 : y=a l_1 ∩l_2 (x/3)+(a/3)=2x ⇒ x=(a/5); y=((2a)/5) pink area ∫_0 ^(a/5) l_2 dx+∫_(a/5) ^a l_1 dx=[x^2 ]_0 ^(a/5) +[(x^2 /6)+((ax)/3)]_(a/5) ^a =((7a^2 )/(15)) grey area ∫_0 ^(a/5) (l_3 −l_1 )dx+∫_(a/5) ^(a/2) (l_3 −l_2 )dx=[((2ax)/3)−(x^2 /6)]_0 ^(a/5) +[ax−x^2 ]_(a/5) ^(a/2) =((13a^2 )/(60)) ((13a^2 )/(60))=13 ⇒ a=2(√(15)) ⇒ ((7a^2 )/(15))=28](Q40646.png)
Commented by Tawa1 last updated on 25/Jul/18

Answered by MrW3 last updated on 26/Jul/18
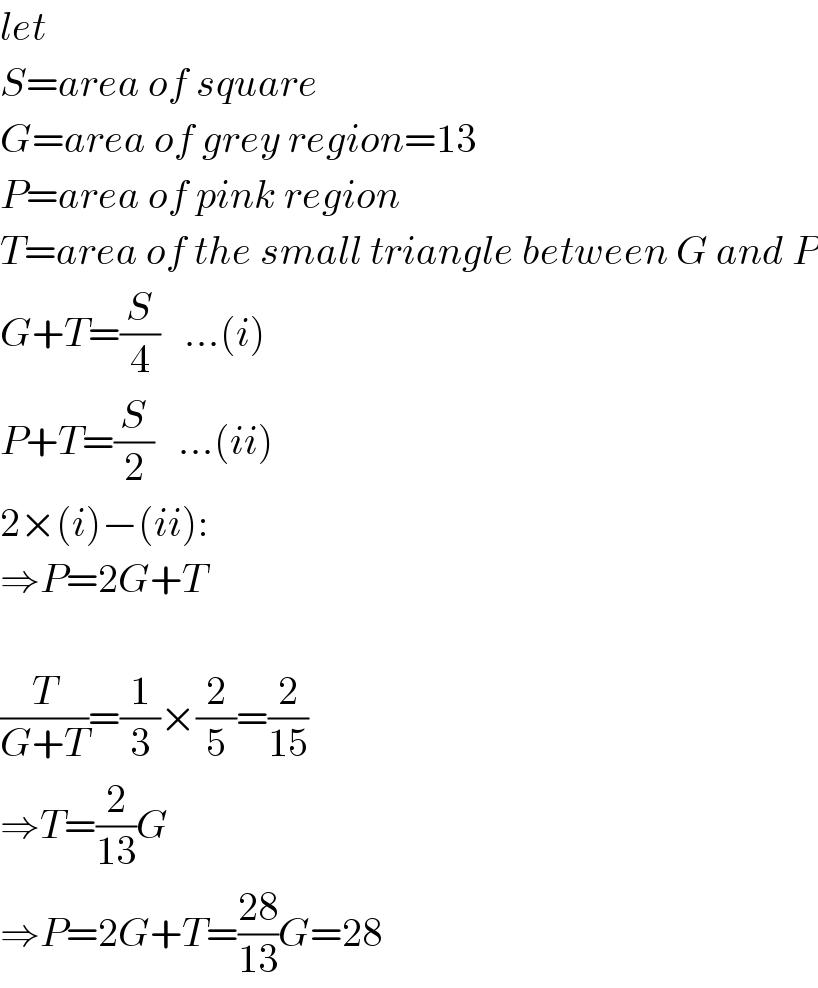
| ||
Question and Answers Forum | ||
Question Number 40637 by Tawa1 last updated on 25/Jul/18 | ||
 | ||
Answered by MJS last updated on 25/Jul/18 | ||
![l_1 : y=(x/3)+(a/3) l_2 : y=2x l_3 : y=a l_1 ∩l_2 (x/3)+(a/3)=2x ⇒ x=(a/5); y=((2a)/5) pink area ∫_0 ^(a/5) l_2 dx+∫_(a/5) ^a l_1 dx=[x^2 ]_0 ^(a/5) +[(x^2 /6)+((ax)/3)]_(a/5) ^a =((7a^2 )/(15)) grey area ∫_0 ^(a/5) (l_3 −l_1 )dx+∫_(a/5) ^(a/2) (l_3 −l_2 )dx=[((2ax)/3)−(x^2 /6)]_0 ^(a/5) +[ax−x^2 ]_(a/5) ^(a/2) =((13a^2 )/(60)) ((13a^2 )/(60))=13 ⇒ a=2(√(15)) ⇒ ((7a^2 )/(15))=28](Q40646.png) | ||
| ||
Commented by Tawa1 last updated on 25/Jul/18 | ||
 | ||
Answered by MrW3 last updated on 26/Jul/18 | ||
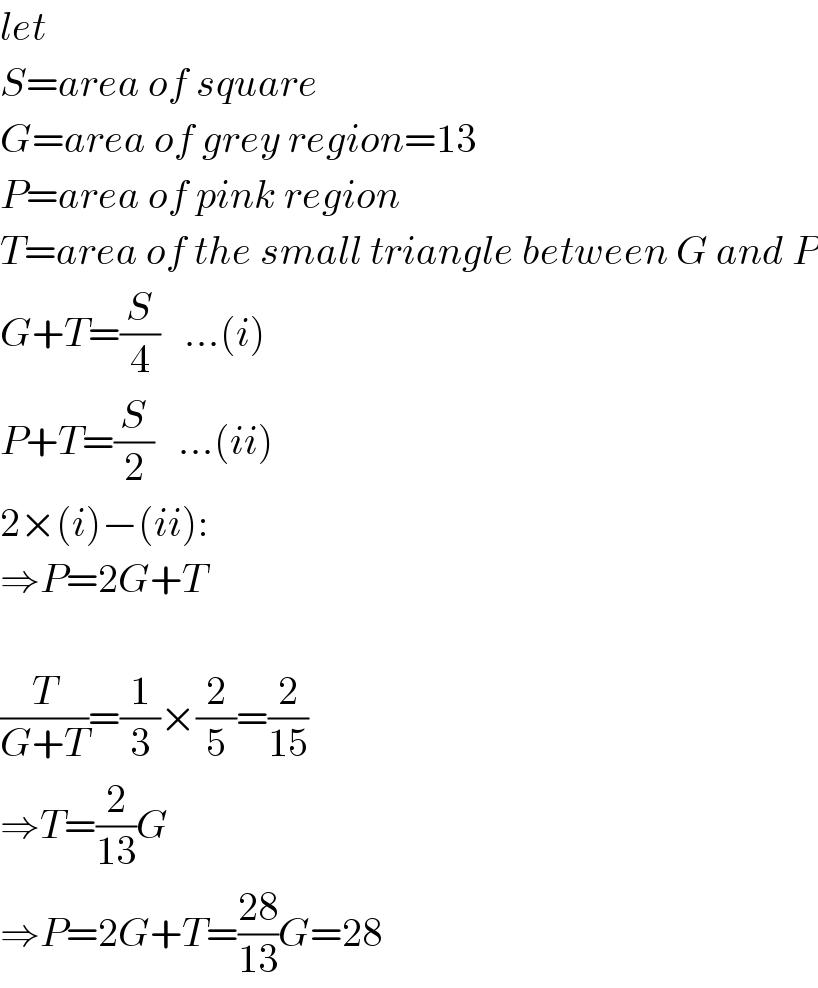 | ||
| ||