Question Number 40787 by rahul 19 last updated on 27/Jul/18
$$\mathrm{Let}\:\mathrm{I}_{\mathrm{1}} =\:\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \frac{\mathrm{sin}\:{x}}{{x}}\:{dx}\:\:,\:\:\mathrm{I}_{\mathrm{2}} =\:\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \frac{\mathrm{sin}\:\left(\mathrm{sin}\:{x}\right)}{\mathrm{sin}\:{x}}{dx} \\ $$ $$,\:\mathrm{I}_{\mathrm{3}} =\:\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \frac{\mathrm{sin}\:\left(\mathrm{tan}\:{x}\right)}{\mathrm{tan}\:{x}}{dx}.\: \\ $$ $${P}\mathrm{rove}\:\mathrm{that}\:\mathrm{I}_{\mathrm{2}} \:>\:\mathrm{I}_{\mathrm{1}} \:>\:\mathrm{I}_{\mathrm{3}} \:. \\ $$
Commented bytanmay.chaudhury50@gmail.com last updated on 27/Jul/18
$${f}\left({x}\right)=\frac{{sinx}}{{x}}\:\:\:{g}\left({x}\right)=\frac{{sin}\left({sinx}\right)}{{sinx}}\:\:\:{h}\left({x}\right)=\frac{{sin}\left({tanx}\right)}{{tanx}} \\ $$ $${to}\:{prove}\:{I}_{\mathrm{2}} >{I}_{\mathrm{1}} >{I}_{\mathrm{3}} \\ $$ $${we}\:{have}\:{to}\:{prove} \\ $$ $$\:{g}\left({x}\right)>{f}\left({x}\right)>{h}\left({x}\right)\:\:\:{when}\:\:\:\frac{\Pi}{\mathrm{3}}>{x}>\frac{\Pi}{\mathrm{6}} \\ $$ $${takining}\:{the}\:{help}\:{of}\:{graph}\:{i}\:{am}\:{trying}\:{to} \\ $$ $${establish}...{later}\:{by}\:{mathematically} \\ $$ $$ \\ $$
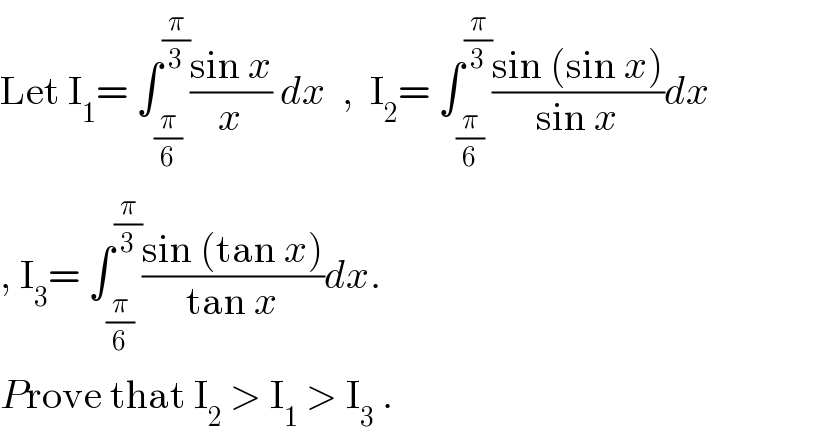
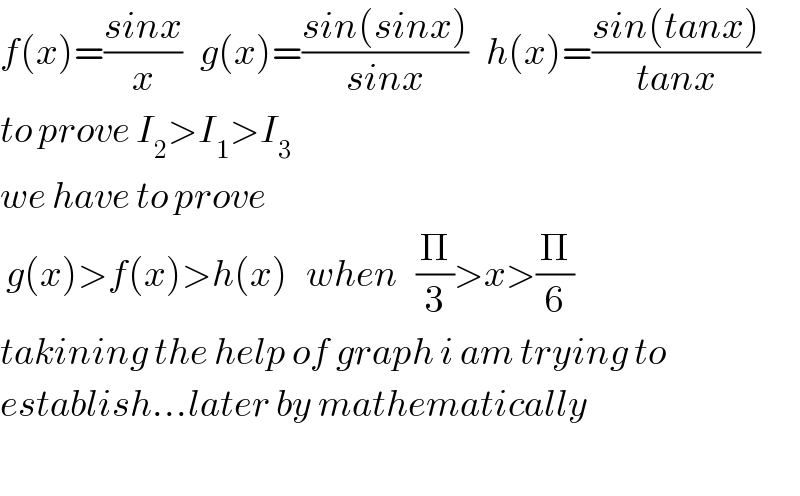
Commented bytanmay.chaudhury50@gmail.com last updated on 27/Jul/18
Commented bytanmay.chaudhury50@gmail.com last updated on 28/Jul/18
$$\:{i}\:{am}\:{attaching}\:{some}\:{thing}\:{refreshing}... \\ $$
Commented bytanmay.chaudhury50@gmail.com last updated on 28/Jul/18
Answered by MJS last updated on 27/Jul/18
![the integrals represent the areas between the functions and the x−axis. so all we have to show is u((sin sin x)/(sin x))≥((sin x)/x)≤((sin tan x)/(tan x)) ∀x∈[(π/6); (π/3)] for x=(π/6) we get 2sin (1/2)≥(3/π)≥(√3)sin ((√3)/3) .958...≥.954...≥.945... for x=(π/3) we get ((2(√3))/3)sin ((√3)/2)≥((3(√3))/(2π))≥((√3)/3)sin (√3) .87...≥.82...≥.56... we have to show that the functions are falling within the given interval (they don′t have any ♮jumpsε or ♮holesε) x∈[(π/6); (π/3)] ⇒ ⇒ sin x ∈[(1/2); ((√3)/2)] ⇒ sin sin x is increasing ⇒ tan x ∈[((√3)/3); (√3)] ⇒ sin tan x is increasing both without any salience the denominators x, sin x and tan x have no zeros in the given intervall ⇒ try to find the amount of increasement in the interval (∫f′(x)dx=f(x)) [((sin sin x)/(sin x))]_(π/6) ^(π/3) ≈−.079 [((sin x)/x)]_(π/6) ^(π/3) ≈−.128 [((sin tan x)/(tan x))]_(π/6) ^(π/3) ≈−.376 so those who start at a lower value loose more along the way ⇒ this should be proven or simply plot them ;−)](Q40795.png)
$$\mathrm{the}\:\mathrm{integrals}\:\mathrm{represent}\:\mathrm{the}\:\mathrm{areas}\:\mathrm{between} \\ $$ $$\mathrm{the}\:\mathrm{functions}\:\mathrm{and}\:\mathrm{the}\:{x}−\mathrm{axis}. \\ $$ $$\mathrm{so}\:\mathrm{all}\:\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{show}\:\mathrm{is} \\ $$ $${u}\frac{\mathrm{sin}\:\mathrm{sin}\:{x}}{\mathrm{sin}\:{x}}\geqslant\frac{\mathrm{sin}\:{x}}{{x}}\leqslant\frac{\mathrm{sin}\:\mathrm{tan}\:{x}}{\mathrm{tan}\:{x}}\:\forall{x}\in\left[\frac{\pi}{\mathrm{6}};\:\frac{\pi}{\mathrm{3}}\right] \\ $$ $$\mathrm{for}\:{x}=\frac{\pi}{\mathrm{6}}\:\mathrm{we}\:\mathrm{get} \\ $$ $$\mathrm{2sin}\:\frac{\mathrm{1}}{\mathrm{2}}\geqslant\frac{\mathrm{3}}{\pi}\geqslant\sqrt{\mathrm{3}}\mathrm{sin}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$ $$.\mathrm{958}...\geqslant.\mathrm{954}...\geqslant.\mathrm{945}... \\ $$ $$\mathrm{for}\:{x}=\frac{\pi}{\mathrm{3}}\:\mathrm{we}\:\mathrm{get} \\ $$ $$\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{sin}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\geqslant\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}\pi}\geqslant\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{sin}\:\sqrt{\mathrm{3}} \\ $$ $$.\mathrm{87}...\geqslant.\mathrm{82}...\geqslant.\mathrm{56}... \\ $$ $$ \\ $$ $$\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{show}\:\mathrm{that}\:\mathrm{the}\:\mathrm{functions}\:\mathrm{are} \\ $$ $$\mathrm{falling}\:\mathrm{within}\:\mathrm{the}\:\mathrm{given}\:\mathrm{interval}\:\left(\mathrm{they}\:\mathrm{don}'\mathrm{t}\right. \\ $$ $$\left.\mathrm{have}\:\mathrm{any}\:\natural\mathrm{jumps}\varepsilon\:\mathrm{or}\:\natural\mathrm{holes}\varepsilon\right) \\ $$ $${x}\in\left[\frac{\pi}{\mathrm{6}};\:\frac{\pi}{\mathrm{3}}\right]\:\Rightarrow \\ $$ $$\:\:\:\:\:\Rightarrow\:\mathrm{sin}\:{x}\:\in\left[\frac{\mathrm{1}}{\mathrm{2}};\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right]\:\Rightarrow\:\mathrm{sin}\:\mathrm{sin}\:{x}\:\:\mathrm{is}\:\mathrm{increasing} \\ $$ $$\:\:\:\:\:\Rightarrow\:\mathrm{tan}\:{x}\:\in\left[\frac{\sqrt{\mathrm{3}}}{\mathrm{3}};\:\sqrt{\mathrm{3}}\right]\:\Rightarrow\:\mathrm{sin}\:\mathrm{tan}\:{x}\:\:\mathrm{is}\:\mathrm{increasing} \\ $$ $$\mathrm{both}\:\mathrm{without}\:\mathrm{any}\:\mathrm{salience} \\ $$ $$\mathrm{the}\:\mathrm{denominators}\:{x},\:\mathrm{sin}\:{x}\:\mathrm{and}\:\mathrm{tan}\:{x}\:\mathrm{have}\:\mathrm{no} \\ $$ $$\mathrm{zeros}\:\mathrm{in}\:\mathrm{the}\:\mathrm{given}\:\mathrm{intervall} \\ $$ $$\Rightarrow\:\mathrm{try}\:\mathrm{to}\:\mathrm{find}\:\mathrm{the}\:\mathrm{amount}\:\mathrm{of}\:\mathrm{increasement} \\ $$ $$\mathrm{in}\:\mathrm{the}\:\mathrm{interval} \\ $$ $$\left(\int{f}'\left({x}\right){dx}={f}\left({x}\right)\right) \\ $$ $$\left[\frac{\mathrm{sin}\:\mathrm{sin}\:{x}}{\mathrm{sin}\:{x}}\right]_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \approx−.\mathrm{079} \\ $$ $$\left[\frac{\mathrm{sin}\:{x}}{{x}}\right]_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \approx−.\mathrm{128} \\ $$ $$\left[\frac{\mathrm{sin}\:\mathrm{tan}\:{x}}{\mathrm{tan}\:{x}}\right]_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \approx−.\mathrm{376} \\ $$ $$\mathrm{so}\:\mathrm{those}\:\mathrm{who}\:\mathrm{start}\:\mathrm{at}\:\mathrm{a}\:\mathrm{lower}\:\mathrm{value}\:\mathrm{loose} \\ $$ $$\mathrm{more}\:\mathrm{along}\:\mathrm{the}\:\mathrm{way}\:\Rightarrow\:\mathrm{this}\:\mathrm{should}\:\mathrm{be}\:\mathrm{proven} \\ $$ $$ \\ $$ $$\left.\mathrm{or}\:\mathrm{simply}\:\mathrm{plot}\:\mathrm{them}\:;−\right) \\ $$