calculate ∫_0 ^(π/2) (x/(sinx))dx .


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 40868 by math khazana by abdo last updated on 28/Jul/18

$c a l c u l a t e \int_{0}^{\frac{π}{2}} \frac{x}{s i n x} d x .$
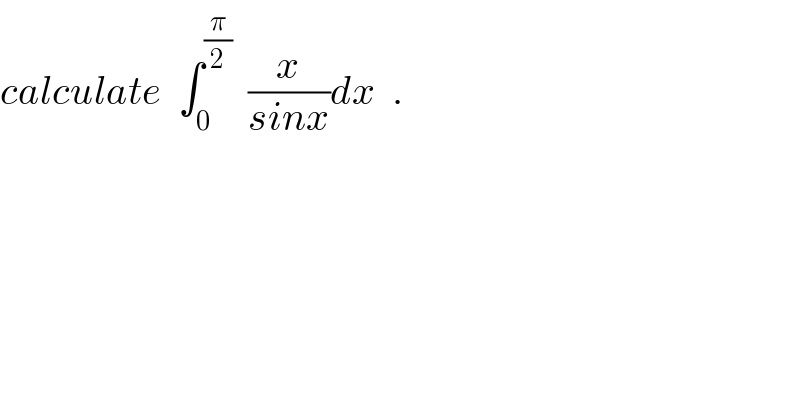
Commented by tanmay.chaudhury50@gmail.com last updated on 29/Jul/18

Commented by tanmay.chaudhury50@gmail.com last updated on 29/Jul/18

$\frac{Π}{2} = 1.57 s o 0 < \int_{0}^{\frac{Π}{2}} \frac{x}{s i n x} ⩽ 18 p l s c h e c k$
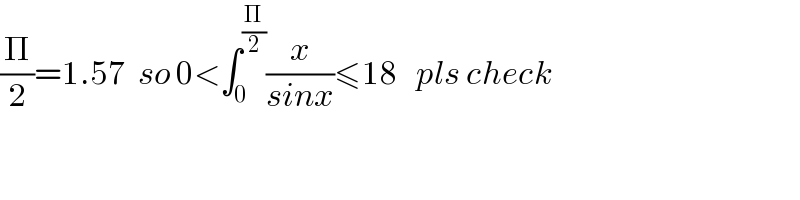
Commented by maxmathsup by imad last updated on 29/Jul/18

$t h e Q i s c a l c u l a t e \int_{\frac{π}{3}}^{\frac{π}{2}} \frac{x}{s i n x} d x .$
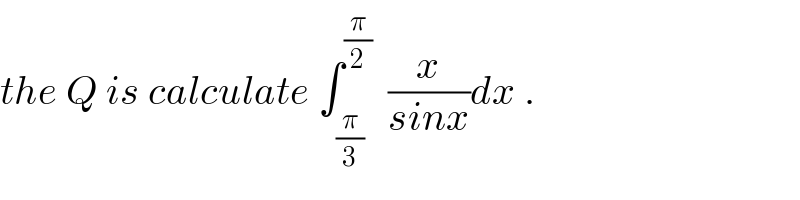
Commented by math khazana by abdo last updated on 30/Jul/18
$let I = ∫_(π/3) ^(π/2) (x/(sinx))dx changement tan((x/2))=t give I = ∫_(1/(√3)) ^1 ((2arctant)/((2t)/(1+t^2 ))) ((2dt)/(1+t^2 )) =2 ∫_(1/(√3)) ^1 ((arctant)/t) dt let introduce the parametric function f(x) = ∫_(1/(√3)) ^1 ((arctan(xt))/t)dt we have f^′ (x)= ∫_(1/(√3)) ^1 (t/(t(1+x^2 t^2 )))dt =∫_(1/(√3)) ^1 (dt/(1+x^2 t^2 )) =_(xt=u) ∫_(x/(√3)) ^x (1/(1+u^2 )) (du/x) =(1/x) ∫_(x/(√3)) ^x (du/(1+u^2 )) =(1/x)[arctan(u)]_(x/(√3)) ^x =(1/x){arctan(x)−arctan((x/(√3)))}⇒ f(x)= ∫_0 ^x ((arctan(t))/t)dt −∫_0 ^x ((arctan((t/(√3))))/t)dt +λ λ=f(0)=0 but ∫_0 ^x ((arctan((t/(√3))))/t)dt =_((t/(√3))=u) ∫_0 ^(x/(√3)) ((arctan(u))/(u(√3))) (√3)du =∫_0 ^(x/(√3)) ((arctan(t))/t)dt⇒ f(x)= ∫_0 ^x ((arctan(t))/t)dt−∫_0 ^(x/(√3)) ((arctan(t))/t)dt I =2f(1) =2{ ∫_0 ^1 ((arctant)/t)dt −∫_0 ^(1/(√3)) ((arctant)/t)dt} we have arctan^′ (t)=(1/(1+t^2 )) =Σ_(n=0) ^∞ (−1)^n t^(2n) ⇒ arctant = Σ_(n=0) ^∞ (((−1)^n )/(2n+1))t^(2n+1) ⇒ ((arctant)/t) =Σ_(n=0) ^∞ (((−1)^n )/(2n+1)) t^(2n) ⇒ ∫_0 ^1 ((arctant)/t)dt =Σ_(n=0) ^∞ (((−1)^n )/(2n+1))∫_0 ^1 t^(2n) dt =Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^2 )) (sum knownby fourier serie) ∫_0 ^(1/(√3)) ((arctant)/t)dt =Σ_(n=0) ^∞ (((−1)^n )/((n+1+))[(1/(2n+1))t^(2n+1) ]_0 ^(1/(√3)) =Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^2 )) ((1/(√3)))^(2n+1) ...$
$l e t I = \int_{\frac{π}{3}}^{\frac{π}{2}} \frac{x}{s i n x} d x c h a n g e m e n t t a n (\frac{x}{2}) = t g i v e$ $I = \int_{\frac{1}{\sqrt{3}}}^{1} \frac{2 a r c t a n t}{\frac{2 t}{1 + t^{2}}} \frac{2 d t}{1 + t^{2}} = 2 \int_{\frac{1}{\sqrt{3}}}^{1} \frac{a r c t a n t}{t} d t$ $l e t i n t r o d u c e t h e p a r a m e t r i c f u n c t i o n$ $f (x) = \int_{\frac{1}{\sqrt{3}}}^{1} \frac{a r c t a n (x t)}{t} d t w e h a v e$ $f^{^{'}} (x) = \int_{\frac{1}{\sqrt{3}}}^{1} \frac{t}{t (1 + x^{2} t^{2})} d t = \int_{\frac{1}{\sqrt{3}}}^{1} \frac{d t}{1 + x^{2} t^{2}}$ $=_{x t = u} \int_{\frac{x}{\sqrt{3}}}^{x} \frac{1}{1 + u^{2}} \frac{d u}{x} = \frac{1}{x} \int_{\frac{x}{\sqrt{3}}}^{x} \frac{d u}{1 + u^{2}}$ $= \frac{1}{x} {[a r c t a n (u)]}_{\frac{x}{\sqrt{3}}}^{x} = \frac{1}{x} {a r c t a n (x) - a r c t a n (\frac{x}{\sqrt{3}})} \Rightarrow$ $f (x) = \int_{0}^{x} \frac{a r c t a n (t)}{t} d t - \int_{0}^{x} \frac{a r c t a n (\frac{t}{\sqrt{3}})}{t} d t + λ$ $λ = f (0) = 0 b u t \int_{0}^{x} \frac{a r c t a n (\frac{t}{\sqrt{3}})}{t} d t$ $=_{\frac{t}{\sqrt{3}} = u} \int_{0}^{\frac{x}{\sqrt{3}}} \frac{a r c t a n (u)}{u \sqrt{3}} \sqrt{3} d u = \int_{0}^{\frac{x}{\sqrt{3}}} \frac{a r c t a n (t)}{t} d t \Rightarrow$ $f (x) = \int_{0}^{x} \frac{a r c t a n (t)}{t} d t - \int_{0}^{\frac{x}{\sqrt{3}}} \frac{a r c t a n (t)}{t} d t$ $I = 2 f (1) = 2 {\int_{0}^{1} \frac{a r c t a n t}{t} d t - \int_{0}^{\frac{1}{\sqrt{3}}} \frac{a r c t a n t}{t} d t}$ $w e h a v e {a r c t a n}^{^{'}} (t) = \frac{1}{1 + t^{2}} = \sum_{n = 0}^{\infty} {(- 1)}^{n} t^{2 n} \Rightarrow$ $a r c t a n t = \sum_{n = 0}^{\infty} \frac{{(- 1)}^{n}}{2 n + 1} t^{2 n + 1} \Rightarrow$ $\frac{a r c t a n t}{t} = \sum_{n = 0}^{\infty} \frac{{(- 1)}^{n}}{2 n + 1} t^{2 n} \Rightarrow$ $\int_{0}^{1} \frac{a r c t a n t}{t} d t = \sum_{n = 0}^{\infty} \frac{{(- 1)}^{n}}{2 n + 1} \int_{0}^{1} t^{2 n} d t$ $= \sum_{n = 0}^{\infty} \frac{{(- 1)}^{n}}{{(2 n + 1)}^{2}} (s u m k n o w n b y f o u r i e r s e r i e)$ $\int_{0}^{\frac{1}{\sqrt{3}}} \frac{a r c t a n t}{t} d t = \sum_{n = 0}^{\infty} \frac{{(- 1)}^{n}}{(n + 1 +} {[\frac{1}{2 n + 1} t^{2 n + 1}]}_{0}^{\frac{1}{\sqrt{3}}}$ $= \sum_{n = 0}^{\infty} \frac{{(- 1)}^{n}}{{(2 n + 1)}^{2}} {(\frac{1}{\sqrt{3}})}^{2 n + 1} . . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum