
Previous in Relation and Functions Next in Relation and Functions
Question Number 40885 by prof Abdo imad last updated on 28/Jul/18
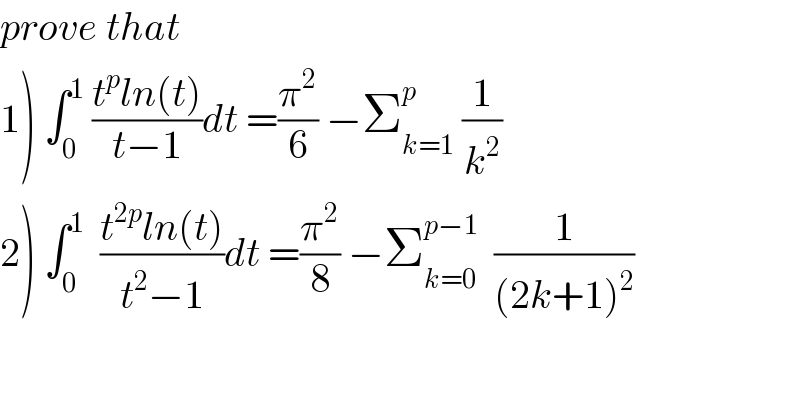
$${prove}\:{that} \\ $$$$\left.\mathrm{1}\right)\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{t}^{{p}} {ln}\left({t}\right)}{{t}−\mathrm{1}}{dt}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:−\sum_{{k}=\mathrm{1}} ^{{p}} \:\frac{\mathrm{1}}{{k}^{\mathrm{2}} } \\ $$$$\left.\mathrm{2}\right)\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{t}^{\mathrm{2}{p}} {ln}\left({t}\right)}{{t}^{\mathrm{2}} −\mathrm{1}}{dt}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:−\sum_{{k}=\mathrm{0}} ^{{p}−\mathrm{1}} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$
Commented by math khazana by abdo last updated on 02/Aug/18
![1) ∫_0 ^1 ((t^p ln(t))/(t−1)) dt =−∫_0 ^1 t^p ln(t)(Σ_(n=0) ^∞ t^n ))dt =−Σ_(n=0) ^∞ ∫_0 ^1 t^(n+p) ln(t) dt =−Σ_(n=0) ^∞ A_n and by parts A_n =∫_0 ^1 t^(n+p) ln(t)dt =[(1/(n+p+1))t^(n+p+1) ln(t)]_0 ^1 −∫_0 ^1 (1/(n+p+1)) t^(n+p) dt =−(1/((n+p+1)^2 )) ⇒−Σ_(n=0) ^∞ A_n =Σ_(n=0) ^∞ (1/((n+p+1)^2 )) =_(n+p+1=k) Σ_(k=p+1) ^∞ (1/k^2 ) but Σ_(k=1) ^∞ (1/k^2 ) =(π^2 /6) =Σ_(k=1) ^p (1/k^2 ) +Σ_(k=p+1) ^∞ (1/k^2 ) ⇒ Σ_(k=p+1) ^∞ =(π^2 /6) −Σ_(k=1) ^p (1/k^2 ) = ∫_0 ^1 ((t^p ln(t))/(t−1)) dt.](Q41134.png)
$$\left.\mathrm{1}\left.\right)\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{t}^{{p}} {ln}\left({t}\right)}{{t}−\mathrm{1}}\:{dt}\:=−\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{{p}} {ln}\left({t}\right)\left(\sum_{{n}=\mathrm{0}} ^{\infty} {t}^{{n}} \right)\right){dt} \\ $$$$=−\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{{n}+{p}} {ln}\left({t}\right)\:{dt}\:=−\sum_{{n}=\mathrm{0}} ^{\infty} \:{A}_{{n}} \:\:{and}\:{by} \\ $$$${parts}\: \\ $$$${A}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{{n}+{p}} {ln}\left({t}\right){dt}\:=\left[\frac{\mathrm{1}}{{n}+{p}+\mathrm{1}}{t}^{{n}+{p}+\mathrm{1}} {ln}\left({t}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{1}}{{n}+{p}+\mathrm{1}}\:{t}^{{n}+{p}} \:{dt} \\ $$$$=−\frac{\mathrm{1}}{\left({n}+{p}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow−\sum_{{n}=\mathrm{0}} ^{\infty} \:{A}_{{n}} =\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{1}}{\left({n}+{p}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=_{{n}+{p}+\mathrm{1}={k}} \:\:\:\:\sum_{{k}={p}+\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\:\:{but} \\ $$$$\sum_{{k}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\:=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=\sum_{{k}=\mathrm{1}} ^{{p}} \:\:\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\:+\sum_{{k}={p}+\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sum_{{k}={p}+\mathrm{1}} ^{\infty} \:=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:−\sum_{{k}=\mathrm{1}} ^{{p}} \:\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\:\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{t}^{{p}} {ln}\left({t}\right)}{{t}−\mathrm{1}}\:{dt}. \\ $$
