Question and Answers Forum

All Questions      Topic List

Permutation and Combination Questions

Previous in All Question      Next in All Question      

Previous in Permutation and Combination      Next in Permutation and Combination      

Question Number 4103 by prakash jain last updated on 28/Dec/15

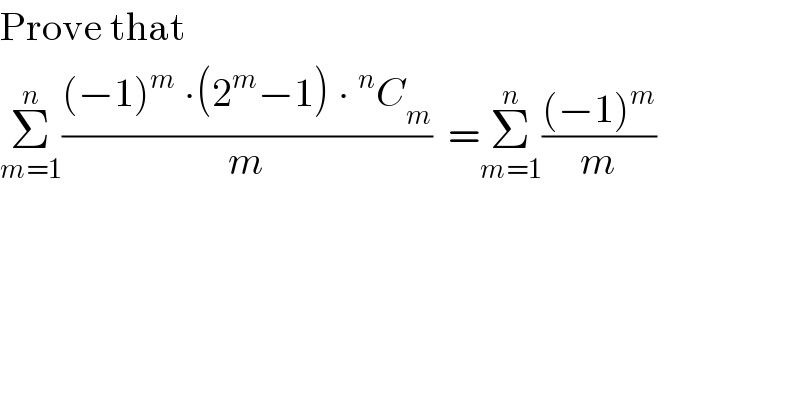
Prove that Σ_(m=1) ^n (((−1)^m ∙(2^m −1) ∙^n C_m )/m) =Σ_(m=1) ^n (((−1)^m )/m)

$$\mathrm{Prove}\:\mathrm{that} \\ $$$$\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{m}} \:\centerdot\left(\mathrm{2}^{{m}} −\mathrm{1}\right)\:\centerdot\:^{{n}} {C}_{{m}} }{{m}}\:\:=\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{m}} }{{m}} \\ $$

Commented by Yozzii last updated on 29/Dec/15

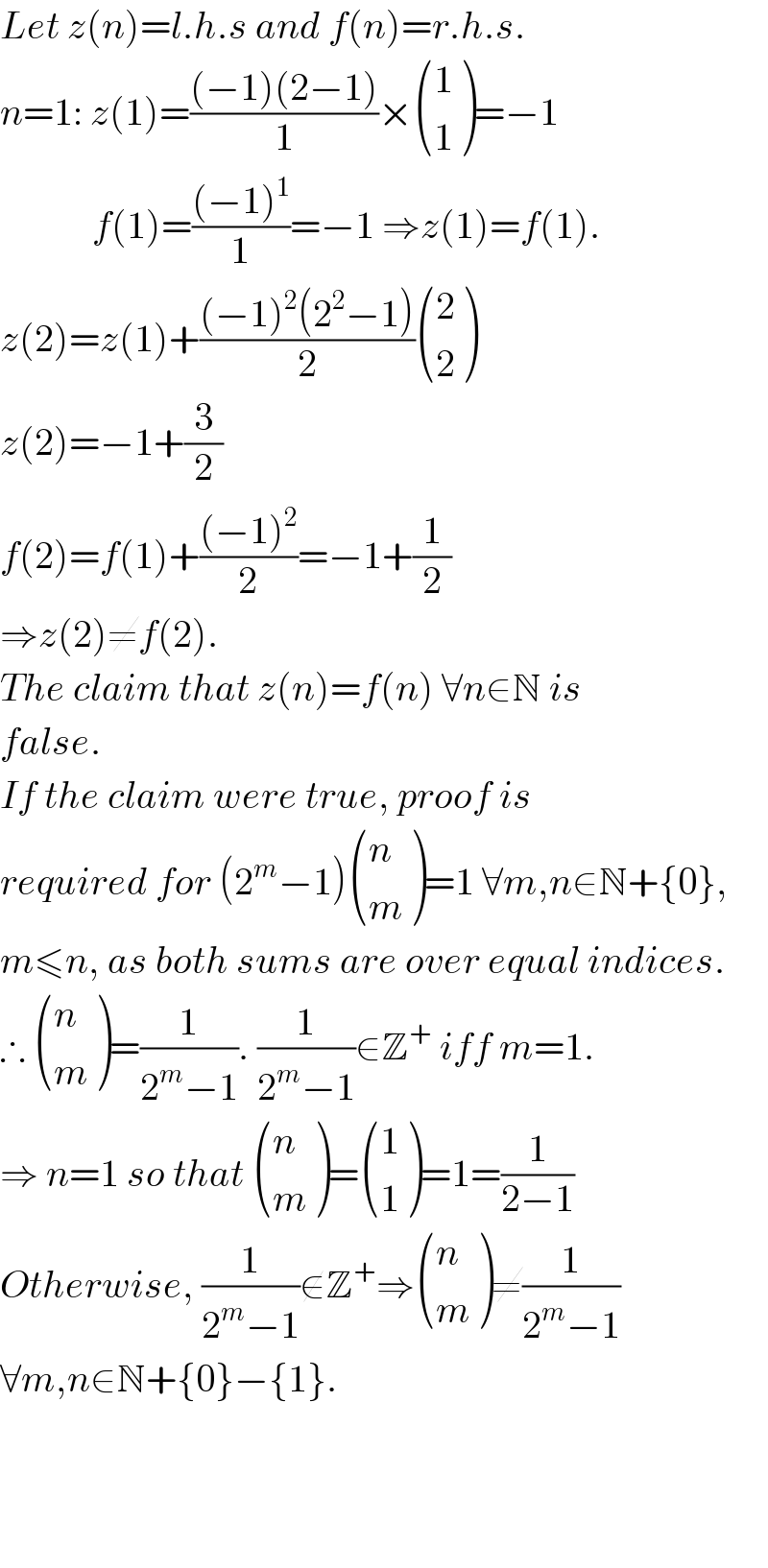
Let z(n)=l.h.s and f(n)=r.h.s. n=1: z(1)=(((−1)(2−1))/1)× ((1),(1) )=−1 f(1)=(((−1)^1 )/1)=−1 ⇒z(1)=f(1). z(2)=z(1)+(((−1)^2 (2^2 −1))/2) ((2),(2) ) z(2)=−1+(3/2) f(2)=f(1)+(((−1)^2 )/2)=−1+(1/2) ⇒z(2)≠f(2). The claim that z(n)=f(n) ∀n∈N is false. If the claim were true, proof is required for (2^m −1) ((n),(m) )=1 ∀m,n∈N+{0}, m≤n, as both sums are over equal indices. ∴ ((n),(m) )=(1/(2^m −1)). (1/(2^m −1))∈Z^+ iff m=1. ⇒ n=1 so that ((n),(m) )= ((1),(1) )=1=(1/(2−1)) Otherwise, (1/(2^m −1))∉Z^+ ⇒ ((n),(m) )≠(1/(2^m −1)) ∀m,n∈N+{0}−{1}.

$${Let}\:{z}\left({n}\right)={l}.{h}.{s}\:{and}\:{f}\left({n}\right)={r}.{h}.{s}. \\ $$$${n}=\mathrm{1}:\:{z}\left(\mathrm{1}\right)=\frac{\left(−\mathrm{1}\right)\left(\mathrm{2}−\mathrm{1}\right)}{\mathrm{1}}×\begin{pmatrix}{\mathrm{1}}\\{\mathrm{1}}\end{pmatrix}=−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{f}\left(\mathrm{1}\right)=\frac{\left(−\mathrm{1}\right)^{\mathrm{1}} }{\mathrm{1}}=−\mathrm{1}\:\Rightarrow{z}\left(\mathrm{1}\right)={f}\left(\mathrm{1}\right). \\ $$$${z}\left(\mathrm{2}\right)={z}\left(\mathrm{1}\right)+\frac{\left(−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{2}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{2}}\begin{pmatrix}{\mathrm{2}}\\{\mathrm{2}}\end{pmatrix} \\ $$$${z}\left(\mathrm{2}\right)=−\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${f}\left(\mathrm{2}\right)={f}\left(\mathrm{1}\right)+\frac{\left(−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}}=−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{z}\left(\mathrm{2}\right)\neq{f}\left(\mathrm{2}\right). \\ $$$${The}\:{claim}\:{that}\:{z}\left({n}\right)={f}\left({n}\right)\:\forall{n}\in\mathbb{N}\:{is} \\ $$$${false}.\: \\ $$$${If}\:{the}\:{claim}\:{were}\:{true},\:{proof}\:{is}\: \\ $$$${required}\:{for}\:\left(\mathrm{2}^{{m}} −\mathrm{1}\right)\begin{pmatrix}{{n}}\\{{m}}\end{pmatrix}=\mathrm{1}\:\forall{m},{n}\in\mathbb{N}+\left\{\mathrm{0}\right\}, \\ $$$${m}\leqslant{n},\:{as}\:{both}\:{sums}\:{are}\:{over}\:{equal}\:{indices}. \\ $$$$\therefore\:\begin{pmatrix}{{n}}\\{{m}}\end{pmatrix}=\frac{\mathrm{1}}{\mathrm{2}^{{m}} −\mathrm{1}}.\:\frac{\mathrm{1}}{\mathrm{2}^{{m}} −\mathrm{1}}\in\mathbb{Z}^{+} \:{iff}\:{m}=\mathrm{1}. \\ $$$$\Rightarrow\:{n}=\mathrm{1}\:{so}\:{that}\:\begin{pmatrix}{{n}}\\{{m}}\end{pmatrix}=\begin{pmatrix}{\mathrm{1}}\\{\mathrm{1}}\end{pmatrix}=\mathrm{1}=\frac{\mathrm{1}}{\mathrm{2}−\mathrm{1}} \\ $$$${Otherwise},\:\frac{\mathrm{1}}{\mathrm{2}^{{m}} −\mathrm{1}}\notin\mathbb{Z}^{+} \Rightarrow\begin{pmatrix}{{n}}\\{{m}}\end{pmatrix}\neq\frac{\mathrm{1}}{\mathrm{2}^{{m}} −\mathrm{1}} \\ $$$$\forall{m},{n}\in\mathbb{N}+\left\{\mathrm{0}\right\}−\left\{\mathrm{1}\right\}. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by prakash jain last updated on 29/Dec/15

I should have made these basic checks before asking for proof. Yozzi had shown in earlier question Q2088. ∫_0 ^(π/4) tan^(2n+1) θdθ=(−1)^n ((1/2)ln2+Σ_(m=1) ^n (((−1)^m )/(2m))) In the same time I did a different integral. ∫_0 ^( π/4) tan^(2n) θtan θdθ =∫_0 ^( π/4) (sec^2 θ−1)^n tan θdθ =(−1)^n ∫_0 ^( π/4) (1−sec^2 θ)^n tan θdθ =(−1)^n ∫_0 ^( π/4) [1+Σ_(m=1) ^n (−1)^m ^n C_m sec^(2m) θ]tan θdθ =(−1)^n ∫_0 ^( π/4) tan θdθ+∫_0 ^( π/4) Σ_(m=1) ^n [(−1)^m ^n C_m sec^(2m−1) θ∙sec θtan θ]dθ =(−1)^n [ln sec θ+Σ_(m=1) ^n (((−1)^m ^n C_m sec^(2m) θ)/(2m))]_0 ^(π/4) =(−1)^n (ln (√2)+Σ_(m=1) ^n (((−1)^m ^n C_m (2^m −1))/(2m))) Now if I compare the two results it looks like. Σ_(m=1) ^n (((−1)^m ^n C_m (2^m −1))/(2m))=Σ_(m=1) ^n (((−1)^m )/(2m)) which is not correct. So where is the error?

$$\mathrm{I}\:\mathrm{should}\:\mathrm{have}\:\mathrm{made}\:\mathrm{these}\:\mathrm{basic}\:\mathrm{checks}\:\mathrm{before} \\ $$$$\mathrm{asking}\:\mathrm{for}\:\mathrm{proof}.\:\mathrm{Yozzi}\:\mathrm{had}\:\mathrm{shown}\:\mathrm{in}\:\mathrm{earlier} \\ $$$$\mathrm{question}\:\mathrm{Q2088}. \\ $$$$\int_{\mathrm{0}} ^{\pi/\mathrm{4}} {tan}^{\mathrm{2}{n}+\mathrm{1}} \theta{d}\theta=\left(−\mathrm{1}\right)^{{n}} \left(\frac{\mathrm{1}}{\mathrm{2}}{ln}\mathrm{2}+\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{m}} }{\mathrm{2}{m}}\right) \\ $$$$\mathrm{In}\:\mathrm{the}\:\mathrm{same}\:\mathrm{time}\:\mathrm{I}\:\mathrm{did}\:\mathrm{a}\:\mathrm{different}\:\mathrm{integral}. \\ $$$$\int_{\mathrm{0}} ^{\:\pi/\mathrm{4}} \mathrm{tan}\:^{\mathrm{2}{n}} \theta\mathrm{tan}\:\theta{d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\:\pi/\mathrm{4}} \left(\mathrm{sec}^{\mathrm{2}} \theta−\mathrm{1}\right)^{{n}} \mathrm{tan}\:\theta{d}\theta \\ $$$$=\left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\:\pi/\mathrm{4}} \left(\mathrm{1}−\mathrm{sec}^{\mathrm{2}} \theta\right)^{{n}} \mathrm{tan}\:\theta{d}\theta \\ $$$$=\left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\:\pi/\mathrm{4}} \left[\mathrm{1}+\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{m}} \:^{{n}} {C}_{{m}} \mathrm{sec}^{\mathrm{2}{m}} \theta\right]\mathrm{tan}\:\theta\mathrm{d}\theta \\ $$$$=\left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\:\pi/\mathrm{4}} \mathrm{tan}\:\theta\mathrm{d}\theta+\int_{\mathrm{0}} ^{\:\pi/\mathrm{4}} \underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\left[\left(−\mathrm{1}\right)^{{m}} \:^{{n}} {C}_{{m}} \mathrm{sec}^{\mathrm{2}{m}−\mathrm{1}} \theta\centerdot\mathrm{sec}\:\theta\mathrm{tan}\:\theta\right]\mathrm{d}\theta \\ $$$$=\left(−\mathrm{1}\right)^{{n}} \left[\mathrm{ln}\:\mathrm{sec}\:\theta+\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{m}} \:^{{n}} {C}_{{m}} \mathrm{sec}\:^{\mathrm{2}{m}} \theta}{\mathrm{2}{m}}\right]_{\mathrm{0}} ^{\pi/\mathrm{4}} \\ $$$$=\left(−\mathrm{1}\right)^{{n}} \left(\mathrm{ln}\:\sqrt{\mathrm{2}}+\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{m}} \:^{{n}} {C}_{{m}} \left(\mathrm{2}^{{m}} −\mathrm{1}\right)}{\mathrm{2}{m}}\right) \\ $$$$\mathrm{Now}\:\mathrm{if}\:\mathrm{I}\:\mathrm{compare}\:\mathrm{the}\:\mathrm{two}\:\mathrm{results}\:\mathrm{it}\:\mathrm{looks}\:\mathrm{like}. \\ $$$$\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{m}} \:^{{n}} {C}_{{m}} \left(\mathrm{2}^{{m}} −\mathrm{1}\right)}{\mathrm{2}{m}}=\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{m}} }{\mathrm{2}{m}} \\ $$$$\mathrm{which}\:\mathrm{is}\:\mathrm{not}\:\mathrm{correct}. \\ $$$$\mathrm{So}\:\mathrm{where}\:\mathrm{is}\:\mathrm{the}\:\mathrm{error}?\: \\ $$

Commented by Yozzii last updated on 29/Dec/15

I recall the question and our discussion on it. I′ll check the working soon.

$${I}\:{recall}\:{the}\:{question}\:{and}\:{our}\: \\ $$$${discussion}\:{on}\:{it}.\:{I}'{ll}\:{check}\:{the}\: \\ $$$${working}\:{soon}. \\ $$

Commented by prakash jain last updated on 29/Dec/15

Thanks. There must be some error in the integral above. I will also recheck.

$$\mathrm{Thanks}.\:\mathrm{There}\:\mathrm{must}\:\mathrm{be}\:\mathrm{some}\:\mathrm{error}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{integral}\:\mathrm{above}.\:\mathrm{I}\:\mathrm{will}\:\mathrm{also}\:\mathrm{recheck}. \\ $$

Commented by Yozzii last updated on 29/Dec/15

I thought that the identity worked inductively but apparently it does not. In other words, you cannot add the nth term to the partial sum of n−1 terms to give the nth partial sum in z(n). For n=2: z(2)=(((−1)^1 (2^1 −1) ((2),(1) ))/1)+(((−1)^2 (2^2 −1) ((2),(2) ))/2) z(2)=−2+(3/2)=((−1)/2)=f(2)=((−1)/1)+(1/2) If done inductively, as detailed above, z(2)=z(1)+(3/2)=(((−1)^1 (2−1) ((1),(1) ))/1)+(3/2)=(1/2)≠f(2) However, the sum Σ_(m=1) ^n (((−1)^m )/m) works inductively. Sorry for my error in my first comment.

$$ \\ $$$${I}\:{thought}\:{that}\:{the}\:{identity}\:{worked} \\ $$$${inductively}\:{but}\:{apparently}\:{it}\:{does}\:{not}. \\ $$$${In}\:{other}\:{words},\:{you}\:{cannot}\:{add}\:{the}\:{nth} \\ $$$${term}\:{to}\:{the}\:{partial}\:{sum}\:{of}\:{n}−\mathrm{1}\:{terms} \\ $$$${to}\:{give}\:{the}\:{nth}\:{partial}\:{sum}\:{in}\:{z}\left({n}\right). \\ $$$${For}\:{n}=\mathrm{2}: \\ $$$${z}\left(\mathrm{2}\right)=\frac{\left(−\mathrm{1}\right)^{\mathrm{1}} \left(\mathrm{2}^{\mathrm{1}} −\mathrm{1}\right)\begin{pmatrix}{\mathrm{2}}\\{\mathrm{1}}\end{pmatrix}}{\mathrm{1}}+\frac{\left(−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{2}^{\mathrm{2}} −\mathrm{1}\right)\begin{pmatrix}{\mathrm{2}}\\{\mathrm{2}}\end{pmatrix}}{\mathrm{2}} \\ $$$${z}\left(\mathrm{2}\right)=−\mathrm{2}+\frac{\mathrm{3}}{\mathrm{2}}=\frac{−\mathrm{1}}{\mathrm{2}}={f}\left(\mathrm{2}\right)=\frac{−\mathrm{1}}{\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$${If}\:{done}\:{inductively},\:{as}\:{detailed}\:{above}, \\ $$$${z}\left(\mathrm{2}\right)={z}\left(\mathrm{1}\right)+\frac{\mathrm{3}}{\mathrm{2}}=\frac{\left(−\mathrm{1}\right)^{\mathrm{1}} \left(\mathrm{2}−\mathrm{1}\right)\begin{pmatrix}{\mathrm{1}}\\{\mathrm{1}}\end{pmatrix}}{\mathrm{1}}+\frac{\mathrm{3}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\neq{f}\left(\mathrm{2}\right) \\ $$$${However},\:{the}\:{sum}\:\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{m}} }{{m}}\:{works} \\ $$$${inductively}. \\ $$$$ \\ $$$${Sorry}\:{for}\:{my}\:{error}\:{in}\:{my}\:{first}\:{comment}. \\ $$$$ \\ $$$$ \\ $$

Commented by prakash jain last updated on 29/Dec/15

Ok. So the assertion in question is not disproved. I also did some computer test for very large n and both LHS and RHS converged to −ln 2. Is there a way to prove the statement in question?

$$\mathrm{Ok}.\:\mathrm{So}\:\mathrm{the}\:\mathrm{assertion}\:\mathrm{in}\:\mathrm{question}\:\mathrm{is}\:\mathrm{not} \\ $$$$\mathrm{disproved}. \\ $$$$\mathrm{I}\:\mathrm{also}\:\mathrm{did}\:\mathrm{some}\:\mathrm{computer}\:\mathrm{test}\:\mathrm{for}\:\mathrm{very}\:\mathrm{large} \\ $$$${n}\:\mathrm{and}\:\mathrm{both}\:\mathrm{LHS}\:\mathrm{and}\:\mathrm{RHS}\:\mathrm{converged}\:\mathrm{to}\:−\mathrm{ln}\:\mathrm{2}. \\ $$$$\mathrm{Is}\:\mathrm{there}\:\mathrm{a}\:\mathrm{way}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{the}\:\mathrm{statement}\:\mathrm{in} \\ $$$$\mathrm{question}? \\ $$

Commented by Yozzii last updated on 29/Dec/15

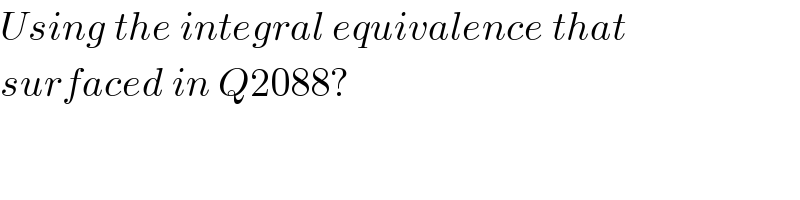
Using the integral equivalence that surfaced in Q2088?

$${Using}\:{the}\:{integral}\:{equivalence}\:{that} \\ $$$${surfaced}\:{in}\:{Q}\mathrm{2088}? \\ $$

Commented by prakash jain last updated on 29/Dec/15

That is an option but without using the integral. Suppose the question is asked as I asked now, it is hard to imagine the integral to prove. I have made a few attempts but could not get a simple proof. May by induction?

$$\mathrm{That}\:\mathrm{is}\:\mathrm{an}\:\mathrm{option}\:\mathrm{but}\:\mathrm{without}\:\mathrm{using}\:\mathrm{the} \\ $$$$\mathrm{integral}.\:\mathrm{Suppose}\:\mathrm{the}\:\mathrm{question}\:\mathrm{is}\:\mathrm{asked}\:\mathrm{as}\:\mathrm{I} \\ $$$$\mathrm{asked}\:\mathrm{now},\:\:\mathrm{it}\:\mathrm{is}\:\mathrm{hard}\:\mathrm{to}\:\mathrm{imagine}\:\mathrm{the}\:\mathrm{integral} \\ $$$$\mathrm{to}\:\mathrm{prove}. \\ $$$$\mathrm{I}\:\mathrm{have}\:\mathrm{made}\:\mathrm{a}\:\mathrm{few}\:\mathrm{attempts}\:\mathrm{but}\:\mathrm{could}\:\mathrm{not} \\ $$$$\mathrm{get}\:\mathrm{a}\:\mathrm{simple}\:\mathrm{proof}.\:\mathrm{May}\:\mathrm{by}\:\mathrm{induction}? \\ $$

Commented by Yozzii last updated on 29/Dec/15

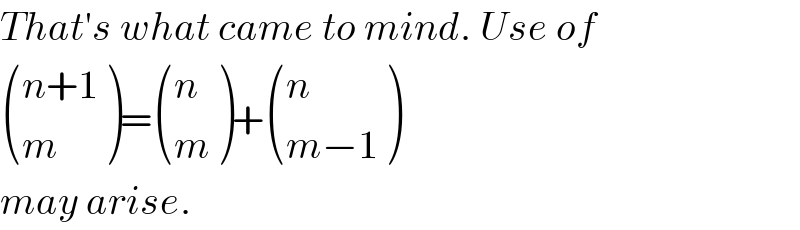
That′s what came to mind. Use of (((n+1)),(m) )= ((n),(m) )+ ((n),((m−1)) ) may arise.

$${That}'{s}\:{what}\:{came}\:{to}\:{mind}.\:{Use}\:{of} \\ $$$$\begin{pmatrix}{{n}+\mathrm{1}}\\{{m}}\end{pmatrix}=\begin{pmatrix}{{n}}\\{{m}}\end{pmatrix}+\begin{pmatrix}{{n}}\\{{m}−\mathrm{1}}\end{pmatrix} \\ $$$${may}\:{arise}.\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com