
Question and Answers Forum
Question Number 41049 by prof Abdo imad last updated on 01/Aug/18
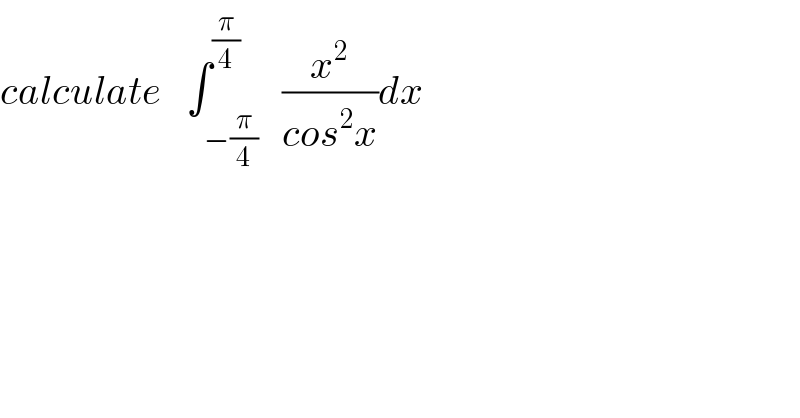
Commented by maxmathsup by imad last updated on 02/Aug/18
![let I = ∫_(−(π/4)) ^(π/4) (x^2 /(cos^2 x))dx ⇒ I =∫_(−(π/4)) ^(π/4) (1+tan^2 x)x^2 dx changement tanx =t give I = ∫_(−1) ^1 (1+t^2 )(arctant)^2 (dt/(1+t^2 )) = 2∫_0 ^1 (arctant)^2 dt by parts I = 2{ [t (arctant)^2 ]_0 ^1 −∫_0 ^1 t ((2arctan(t))/(1+t^2 ))dt} =2{(π^2 /(16)) − ∫_0 ^1 ((2t arctan(t))/(1+t^2 ))} =(π^2 /8) −4 ∫_0 ^1 ((t arctan(t))/(1+t^2 )) dt let ϕ(x) =∫_0 ^1 ((t arctan(xt))/(1+t^2 )) dt ⇒ϕ^′ (x) = ∫_0 ^1 (t^2 /((1+x^2 t^2 )(1+t^2 )))dt ϕ^′ (x) =_(xt =u) ∫_0 ^x (u^2 /(x^2 (1+u^2 )(1+(u^2 /x^2 )))) (du/x) = ∫_0 ^x (u^2 /(x(1+u^2 )(x^2 +u^2 )))du =(1/x) ∫_0 ^1 (u^2 /((u^2 +1)( u^2 +x^2 )))du let decompose F(u) = (u^2 /((u^2 +1)(u^2 +x^2 ))) ⇒F(u) = ((au+b)/(u^2 +1)) +((cu +d)/(u^2 +x^2 )) F(−u) =F(u) ⇒((−au +b)/(u^2 +1)) +((−cu +d)/(u^2 +x^2 )) =F(u) ⇒a=c=0 ⇒ F(u) = (b/(u^2 +1)) +(d/(u^2 +x^2 )) lim_(u→+∞) u^2 F(u) =1 =b+d ⇒d=1−b ⇒ F(u) =(b/(u^2 +1)) +((1−b)/(u^2 +x^2 )) ⇒F(0) =0 =b +((1−b)/x^2 ) =(1/x^2 ) +(1−(1/x^2 ))b ⇒ −(1/x^2 ) =(((x^2 −1)b)/x^2 ) ⇒b =(1/(1−x^2 )) ⇒F(u) =(1/((1−x^2 )(u^2 +1))) +((1−(1/(1−x^2 )))/(u^2 +x^2 )) = (1/((1−x^2 )(u^2 +1))) −(x^2 /((1−x^2 )(u^2 +x^2 ))) ⇒F(u) =(1/(1−x^2 )){(1/(u^2 +1)) −(x^2 /(u^2 +x^2 ))} ϕ^′ (x) =(1/x)∫_0 ^x F(u)du =(1/(x(1−x^2 ))){ ∫_0 ^x (du/(1+u^2 )) −x^2 ∫_0 ^x (du/(u^2 +x^2 ))} =((arctanx)/(x(1−x^2 ))) −(x/(1−x^2 )) ∫_0 ^x (du/(u^2 +x^2 )) but ∫_0 ^x (du/(u^2 +x^2 )) du =_(u=xt) ∫_0 ^1 ((xdt)/(x^2 t^2 +x^2 )) =(1/x) ∫_0 ^1 (dt/(t^2 +1)) =(π/(4x)) ⇒ ϕ^′ (x) = ((arctan(x))/(x(1−x^2 ))) −(π/(4(1−x^2 ))) ( for x^2 ≠1) ⇒](Q41126.png)
Commented by maxmathsup by imad last updated on 02/Aug/18
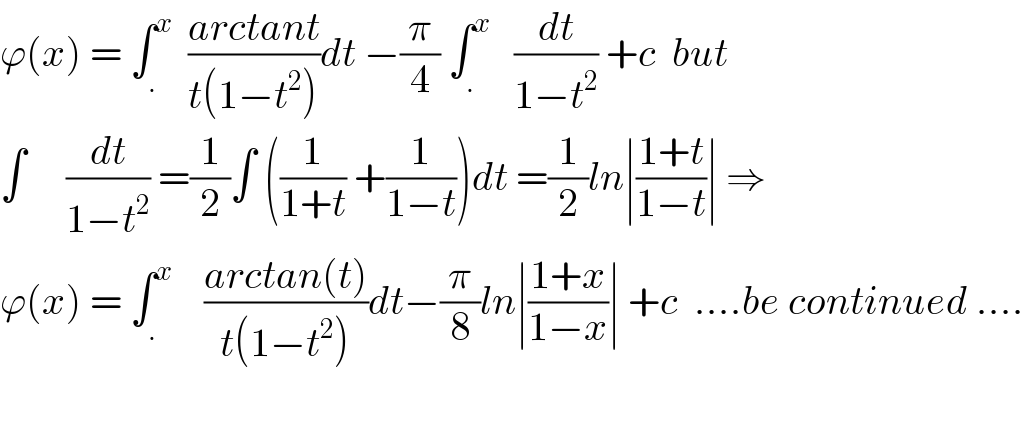
| ||
Question and Answers Forum | ||
Question Number 41049 by prof Abdo imad last updated on 01/Aug/18 | ||
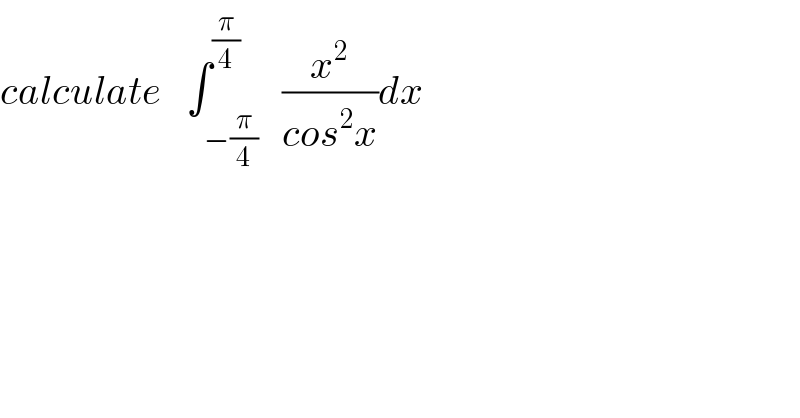 | ||
Commented by maxmathsup by imad last updated on 02/Aug/18 | ||
![let I = ∫_(−(π/4)) ^(π/4) (x^2 /(cos^2 x))dx ⇒ I =∫_(−(π/4)) ^(π/4) (1+tan^2 x)x^2 dx changement tanx =t give I = ∫_(−1) ^1 (1+t^2 )(arctant)^2 (dt/(1+t^2 )) = 2∫_0 ^1 (arctant)^2 dt by parts I = 2{ [t (arctant)^2 ]_0 ^1 −∫_0 ^1 t ((2arctan(t))/(1+t^2 ))dt} =2{(π^2 /(16)) − ∫_0 ^1 ((2t arctan(t))/(1+t^2 ))} =(π^2 /8) −4 ∫_0 ^1 ((t arctan(t))/(1+t^2 )) dt let ϕ(x) =∫_0 ^1 ((t arctan(xt))/(1+t^2 )) dt ⇒ϕ^′ (x) = ∫_0 ^1 (t^2 /((1+x^2 t^2 )(1+t^2 )))dt ϕ^′ (x) =_(xt =u) ∫_0 ^x (u^2 /(x^2 (1+u^2 )(1+(u^2 /x^2 )))) (du/x) = ∫_0 ^x (u^2 /(x(1+u^2 )(x^2 +u^2 )))du =(1/x) ∫_0 ^1 (u^2 /((u^2 +1)( u^2 +x^2 )))du let decompose F(u) = (u^2 /((u^2 +1)(u^2 +x^2 ))) ⇒F(u) = ((au+b)/(u^2 +1)) +((cu +d)/(u^2 +x^2 )) F(−u) =F(u) ⇒((−au +b)/(u^2 +1)) +((−cu +d)/(u^2 +x^2 )) =F(u) ⇒a=c=0 ⇒ F(u) = (b/(u^2 +1)) +(d/(u^2 +x^2 )) lim_(u→+∞) u^2 F(u) =1 =b+d ⇒d=1−b ⇒ F(u) =(b/(u^2 +1)) +((1−b)/(u^2 +x^2 )) ⇒F(0) =0 =b +((1−b)/x^2 ) =(1/x^2 ) +(1−(1/x^2 ))b ⇒ −(1/x^2 ) =(((x^2 −1)b)/x^2 ) ⇒b =(1/(1−x^2 )) ⇒F(u) =(1/((1−x^2 )(u^2 +1))) +((1−(1/(1−x^2 )))/(u^2 +x^2 )) = (1/((1−x^2 )(u^2 +1))) −(x^2 /((1−x^2 )(u^2 +x^2 ))) ⇒F(u) =(1/(1−x^2 )){(1/(u^2 +1)) −(x^2 /(u^2 +x^2 ))} ϕ^′ (x) =(1/x)∫_0 ^x F(u)du =(1/(x(1−x^2 ))){ ∫_0 ^x (du/(1+u^2 )) −x^2 ∫_0 ^x (du/(u^2 +x^2 ))} =((arctanx)/(x(1−x^2 ))) −(x/(1−x^2 )) ∫_0 ^x (du/(u^2 +x^2 )) but ∫_0 ^x (du/(u^2 +x^2 )) du =_(u=xt) ∫_0 ^1 ((xdt)/(x^2 t^2 +x^2 )) =(1/x) ∫_0 ^1 (dt/(t^2 +1)) =(π/(4x)) ⇒ ϕ^′ (x) = ((arctan(x))/(x(1−x^2 ))) −(π/(4(1−x^2 ))) ( for x^2 ≠1) ⇒](Q41126.png) | ||
Commented by maxmathsup by imad last updated on 02/Aug/18 | ||
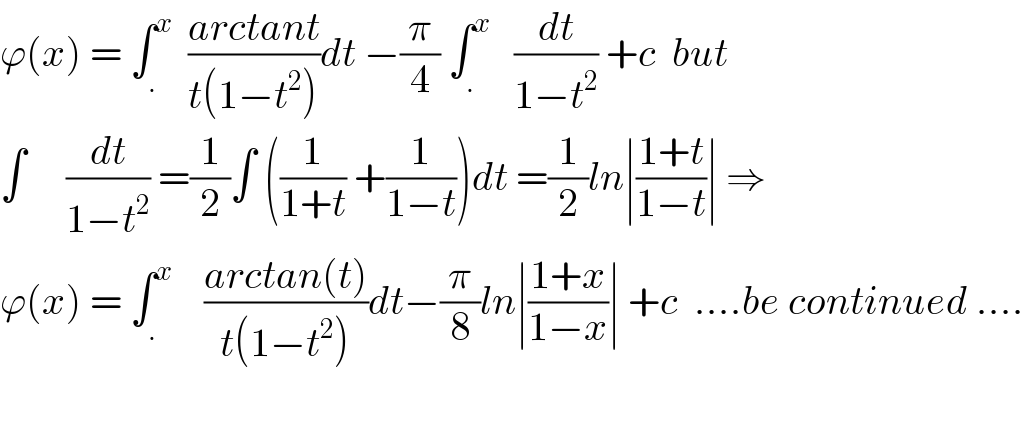 | ||