Math Question and Answers


Question and Answers Forum

All Questions Topic List
Differentiation Questions
Previous in All Question Next in All Question
Previous in Differentiation Next in Differentiation
Question Number 41117 by ajfour last updated on 02/Aug/18

	Answered by MJS last updated on 02/Aug/18
	$r=1 P= ((0),(0) ) A= (((cos α)),((1+sin α)) ) F= (((cos α)),(0) ) ∣AP∣=(√(2(1+sin α))) ∣AF∣=1+sin α ∣FP∣=cos α area=(1/4)(sin 2α +2cos α) (d/dα)[area]=(1/2)(cos 2α −sin α)=0 ⇒ α∈{(π/6), ((5π)/6), ((3π)/2)} area({(π/6), ((5π)/6), ((3π)/2)})={((3(√3))/8), −((3(√3))/8), 0} ⇒ ⇒ α=(π/6), area(AFP)=((3(√3))/8)r^2$
	$r = 1$ $P = (\begin{matrix} 0 \\ 0 \end{matrix}) A = (\begin{matrix} \cos α \\ 1 + \sin α \end{matrix}) F = (\begin{matrix} \cos α \\ 0 \end{matrix})$ $∣ A P ∣= \sqrt{2 (1 + \sin α)}$ $∣ A F ∣= 1 + \sin α$ $∣ F P ∣= \cos α$ $area = \frac{1}{4} (\sin 2 α + 2 \cos α)$ $\frac{d}{d α} [area] = \frac{1}{2} (\cos 2 α - \sin α) = 0 \Rightarrow α \in {\frac{π}{6}, \frac{5 π}{6}, \frac{3 π}{2}}$ $area ({\frac{π}{6}, \frac{5 π}{6}, \frac{3 π}{2}}) = {\frac{3 \sqrt{3}}{8}, - \frac{3 \sqrt{3}}{8}, 0} \Rightarrow$ $\Rightarrow α = \frac{π}{6}, area (A F P) = \frac{3 \sqrt{3}}{8} r^{2}$
	Commented by ajfour last updated on 02/Aug/18

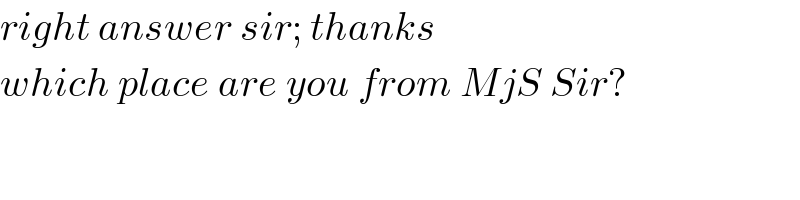
	$r i g h t a n s w e r s i r; t h a n k s$ $w h i c h p l a c e a r e y o u f r o m M j S S i r ?$
	Commented by MJS last updated on 02/Aug/18

	$I^{'} m from Europe / Austria / Vienna$ $most users here seem to be from India$
	Commented by ajfour last updated on 02/Aug/18

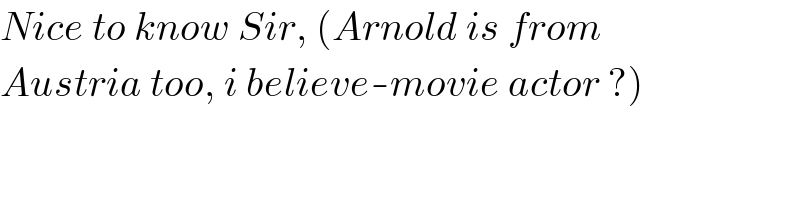
	$N i c e t o k n o w S i r, (A r n o l d i s f r o m$ $A u s t r i a t o o, i b e l i e v e - m o v i e a c t o r ?)$
	Commented by MJS last updated on 02/Aug/18

	$yes . former body - builder and governer of$ $California . . .$ $I^{'} m glad to be un - famous musician and$ $hobby - mathematician . {it}^{'} s a more peaceful$ $life; -)$
	Answered by tanmay.chaudhury50@gmail.com last updated on 02/Aug/18
	$FP=a FA=b area(s)=(1/2)ab o be the centre OP=OA=r FA tangent at P so OPF=90^o let ∠OPA=θ=∠OAP cos(180^o −2θ)=((r^2 +r^2 −PA^2 )/(2r.r)) −2r^2 cos2θ=2r^2 −PA^2 PA^2 =2r^2 +2r^2 cos2θ PA^2 =2r^2 (1+cos2θ) PA=2rcosθ ∠OPF=∠OPA+∠APF=90^o ∠APF=90^o −∠OPA=90^o −θ ∠PAF=θ so sinθ=((PF)/(PA))=(a/(2rcosθ)) a=2rsinθcosθ=rsin2θ cosθ=((AF)/(PA))=(b/(2rcosθ)) so b=2rcos^2 θ^ =r(1+cos2θ) area of triangle=(1/2)ab s =(1/2)rsin2θ.r(1+cos2θ) s=(r^2 /2)(sin2θ)(1+cos2θ) (ds/dθ)=(r^2 /2){sin2θ.−2sin2θ+(1+cos2θ)(cos2θ).2} (ds/dθ)=0 −2sin^2 2θ+2cos2θ+2cos^2 2θ=0 cos4θ+cos2θ=0 2cos3θ.cosθ=0 if cosθ=0 so θ=90^o whichis not feasible so cos3θ=0=cos90^o θ=30^o area max=(r^2 /2)(sin60^o )(1+cos60^o ) =(r^2 /2)(((√3)/2))(1+(1/2))=((3(√3))/8)r^2$
	$F P = a F A = b a r e a (s) = \frac{1}{2} a b$ $o b e t h e c e n t r e O P = O A = r F A t a n g e n t a t P$ $s o O P F = 90^{o} l e t ∠ O P A = θ = ∠ O A P$ $c o s (180^{o} - 2 θ) = \frac{r^{2} + r^{2} - {P A}^{2}}{2 r . r}$ $- 2 r^{2} c o s 2 θ = 2 r^{2} - {P A}^{2}$ ${P A}^{2} = 2 r^{2} + 2 r^{2} c o s 2 θ$ ${P A}^{2} = 2 r^{2} (1 + c o s 2 θ)$ $P A = 2 r c o s θ$ $∠ O P F = ∠ O P A + ∠ A P F = 90^{o}$ $∠ A P F = 90^{o} - ∠ O P A = 90^{o} - θ$ $∠ P A F = θ s o s i n θ = \frac{P F}{P A} = \frac{a}{2 r c o s θ}$ $a = 2 r s i n θ c o s θ = r s i n 2 θ$ $c o s θ = \frac{A F}{P A} = \frac{b}{2 r c o s θ} s o b = 2 {r c o s}^{2} \overset{}{θ} = r (1 + c o s 2 θ)$ $a r e a o f t r i a n g l e = \frac{1}{2} a b$ $s = \frac{1}{2} r s i n 2 θ . r (1 + c o s 2 θ)$ $s = \frac{r^{2}}{2} (s i n 2 θ) (1 + c o s 2 θ)$ $\frac{d s}{d θ} = \frac{r^{2}}{2} {s i n 2 θ . - 2 s i n 2 θ + (1 + c o s 2 θ) (c o s 2 θ) . 2}$ $\frac{d s}{d θ} = 0$ $- 2 {s i n}^{2} 2 θ + 2 c o s 2 θ + 2 {c o s}^{2} 2 θ = 0$ $c o s 4 θ + c o s 2 θ = 0$ $2 c o s 3 θ . c o s θ = 0$ $i f c o s θ = 0 s o θ = 90^{o} w h i c h i s n o t f e a s i b l e$ $s o c o s 3 θ = 0 = c o s 90^{o}$ $θ = 30^{o} a r e a m a x = \frac{r^{2}}{2} (s i n 60^{o}) (1 + c o s 60^{o})$ $= \frac{r^{2}}{2} (\frac{\sqrt{3}}{2}) (1 + \frac{1}{2}) = \frac{3 \sqrt{3}}{8} r^{2}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum