
Question and Answers Forum
Question Number 41135 by math khazana by abdo last updated on 02/Aug/18

Answered by math khazana by abdo last updated on 03/Aug/18
![we have f^′ (x)= ∫_0 ^1 (t/(1+x^2 t^2 ))dt =_(xt =u) ∫_0 ^x (u/(x(1+u^2 ))) (du/x) = (1/x^2 ) ∫_0 ^x ((udu)/(1+u^2 )) =(1/(2x^2 ))[ln(1+u^2 )]_0 ^x =((ln(1+x^2 ))/(2x^2 )) ⇒ f(x) = ∫_0 ^x ((ln(1+t^2 ))/(2t^2 )) dt +c c=f(0) =0 ⇒ f(x)=∫_0 ^x ((ln(1+t^2 ))/(2t^2 )) dt by parts 2f(x)=[−(1/t)ln(1+t^2 )]_0 ^x + ∫_0 ^x (1/t) ((2t)/(1+t^2 ))dt =−(1/x)ln(1+x^2 ) +2arctanx ⇒ f(x)= arctan(x)−(1/(2x))ln(1+x^2 ) .](Q41184.png)
Commented by math khazana by abdo last updated on 03/Aug/18
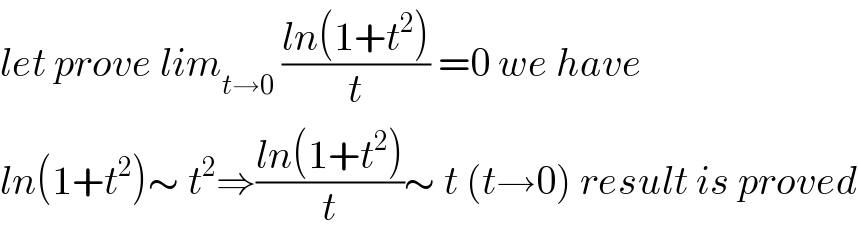
| ||
Question and Answers Forum | ||
Question Number 41135 by math khazana by abdo last updated on 02/Aug/18 | ||
 | ||
Answered by math khazana by abdo last updated on 03/Aug/18 | ||
![we have f^′ (x)= ∫_0 ^1 (t/(1+x^2 t^2 ))dt =_(xt =u) ∫_0 ^x (u/(x(1+u^2 ))) (du/x) = (1/x^2 ) ∫_0 ^x ((udu)/(1+u^2 )) =(1/(2x^2 ))[ln(1+u^2 )]_0 ^x =((ln(1+x^2 ))/(2x^2 )) ⇒ f(x) = ∫_0 ^x ((ln(1+t^2 ))/(2t^2 )) dt +c c=f(0) =0 ⇒ f(x)=∫_0 ^x ((ln(1+t^2 ))/(2t^2 )) dt by parts 2f(x)=[−(1/t)ln(1+t^2 )]_0 ^x + ∫_0 ^x (1/t) ((2t)/(1+t^2 ))dt =−(1/x)ln(1+x^2 ) +2arctanx ⇒ f(x)= arctan(x)−(1/(2x))ln(1+x^2 ) .](Q41184.png) | ||
| ||
Commented by math khazana by abdo last updated on 03/Aug/18 | ||
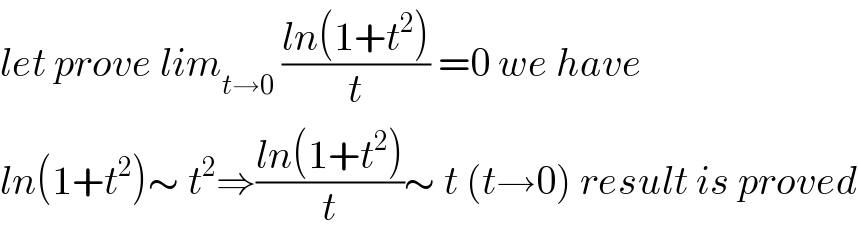 | ||