let f(x)=2x−(√(x−1)) find ∫ f^(−1) (x)dx .


Question and Answers Forum

All Questions Topic List
Relation and Functions Questions
Previous in All Question Next in All Question
Previous in Relation and Functions Next in Relation and Functions
Question Number 41136 by math khazana by abdo last updated on 02/Aug/18

$l e t f (x) = 2 x - \sqrt{x - 1}$ $f i n d \int f^{- 1} (x) d x .$
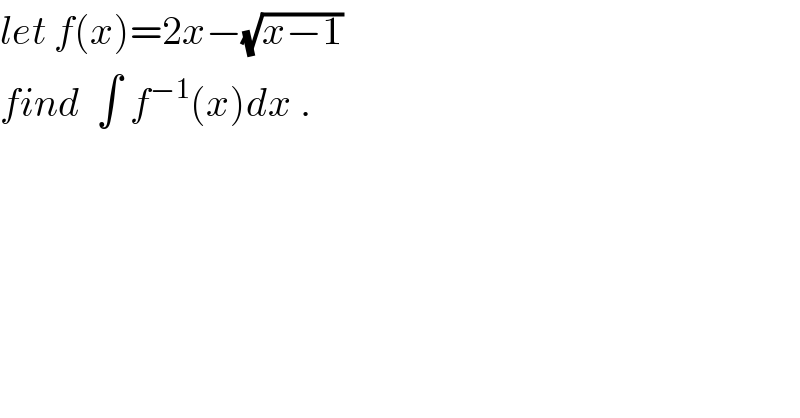
	Answered by MJS last updated on 02/Aug/18
	$f(x) defined for x∈[1; +∞] f′(x)=2−(1/(2(√(x−1))))=0 ⇒ x=((17)/(16)) f′′(x)=(1/(4(x−1)^(3/2) )); f′′(((17)/(16)))=16>0 ⇒ min at ((((17)/(16))),(((15)/8)) ) range(f(x))=[((15)/8); +∞[ x=2y−(√(y−1)) (√(y−1))=2y−x y−1=4y^2 −4xy+x^2 y^2 −(x+(1/4))y+((x^2 +1)/4)=0 y_1 =(x/2)+(1/8)−((√(8x−15))/8) defined for x∈[((15)/8); +∞] y_1 ′=(1/2)−(1/(2(√(8x−15))))=0 ⇒ x=2 y_1 ′′=(2/((8x−15)^(3/2) )); x=2 ⇒ y_2 ′′=2>0 ⇒ min at ((2),(1) ) range=[1; +∞] y_2 =(x/2)+(1/8)+((√(8x−15))/8) defined for x∈[((15)/8); +∞] y_2 ′=(1/2)+(1/(2(√(8x−15))))=0 ⇒ no solution range=[((17)/(16)); +∞] f^(−1) (x)= { (((x/2)+(1/8)−((√(8x−15))/8); x∈[((15)/8); 2])),(((x/2)+(1/8)+((√(8x−15))/8); x∈]((15)/8); +∞[)) :} ∫f^(−1) (x)dx= { (((x^2 /4)+(x/8)−(((8x−15)^(3/2) )/(96)); x∈[((15)/8); 2])),(((x^2 /4)+(x/8)+(((8x−15)^(3/2) )/(96)); x∈]((15)/8); +∞[)) :} but of course if you want the area between this function and the x−axis you must take ∫f^(−1) (x)dx= { (((x^2 /4)+(x/8)−(((8x−15)^(3/2) )/(96)); x∈[((15)/8); 2])),(((x^2 /4)+(x/8)+(((8x−15)^(3/2) )/(96)); x∈]2; +∞[)) :}$
	$f (x) defined for x \in [1; + \infty]$ $f^{'} (x) = 2 - \frac{1}{2 \sqrt{x - 1}} = 0 \Rightarrow x = \frac{17}{16}$ $f^{″} (x) = \frac{1}{4 {(x - 1)}^{\frac{3}{2}}}; f^{″} (\frac{17}{16}) = 16 > 0 \Rightarrow \min at (\begin{matrix} \frac{17}{16} \\ \frac{15}{8} \end{matrix})$ $range (f (x)) = [\frac{15}{8}; + \infty [$ $x = 2 y - \sqrt{y - 1}$ $\sqrt{y - 1} = 2 y - x$ $y - 1 = 4 y^{2} - 4 x y + x^{2}$ $y^{2} - (x + \frac{1}{4}) y + \frac{x^{2} + 1}{4} = 0$ $y_{1} = \frac{x}{2} + \frac{1}{8} - \frac{\sqrt{8 x - 15}}{8}$ $defined for x \in [\frac{15}{8}; + \infty]$ $y_{1}^{'} = \frac{1}{2} - \frac{1}{2 \sqrt{8 x - 15}} = 0 \Rightarrow x = 2$ $y_{1}^{″} = \frac{2}{{(8 x - 15)}^{\frac{3}{2}}}; x = 2 \Rightarrow y_{2}^{″} = 2 > 0 \Rightarrow \min at (\begin{matrix} 2 \\ 1 \end{matrix})$ $range = [1; + \infty]$ $y_{2} = \frac{x}{2} + \frac{1}{8} + \frac{\sqrt{8 x - 15}}{8}$ $defined for x \in [\frac{15}{8}; + \infty]$ $y_{2}^{'} = \frac{1}{2} + \frac{1}{2 \sqrt{8 x - 15}} = 0 \Rightarrow no solution$ $range = [\frac{17}{16}; + \infty]$ $f^{- 1} (x) = {\begin{cases} \frac{x}{2} + \frac{1}{8} - \frac{\sqrt{8 x - 15}}{8}; x \in [\frac{15}{8}; 2] \\ \frac{x}{2} + \frac{1}{8} + \frac{\sqrt{8 x - 15}}{8}; x \in] \frac{15}{8}; + \infty [ \end{cases}$ $\int f^{- 1} (x) d x = {\begin{cases} \frac{x^{2}}{4} + \frac{x}{8} - \frac{{(8 x - 15)}^{\frac{3}{2}}}{96}; x \in [\frac{15}{8}; 2] \\ \frac{x^{2}}{4} + \frac{x}{8} + \frac{{(8 x - 15)}^{\frac{3}{2}}}{96}; x \in] \frac{15}{8}; + \infty [ \end{cases}$ $but of course if you want the area between$ $this function and the x - axis you must take$ $\int f^{- 1} (x) d x = {\begin{cases} \frac{x^{2}}{4} + \frac{x}{8} - \frac{{(8 x - 15)}^{\frac{3}{2}}}{96}; x \in [\frac{15}{8}; 2] \\ \frac{x^{2}}{4} + \frac{x}{8} + \frac{{(8 x - 15)}^{\frac{3}{2}}}{96}; x \in] 2; + \infty [ \end{cases}$
	Commented by math khazana by abdo last updated on 03/Aug/18

	$t h a n k y o u s i r m j s f o r t h i s h a r d w o r k .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum