
Question and Answers Forum
Question Number 41141 by Kishan Daroga last updated on 02/Aug/18
![If X= [(3,(−4)),(1,(−1)) ], the value of X^n is](Q41141.png)
Commented by math khazana by abdo last updated on 04/Aug/18
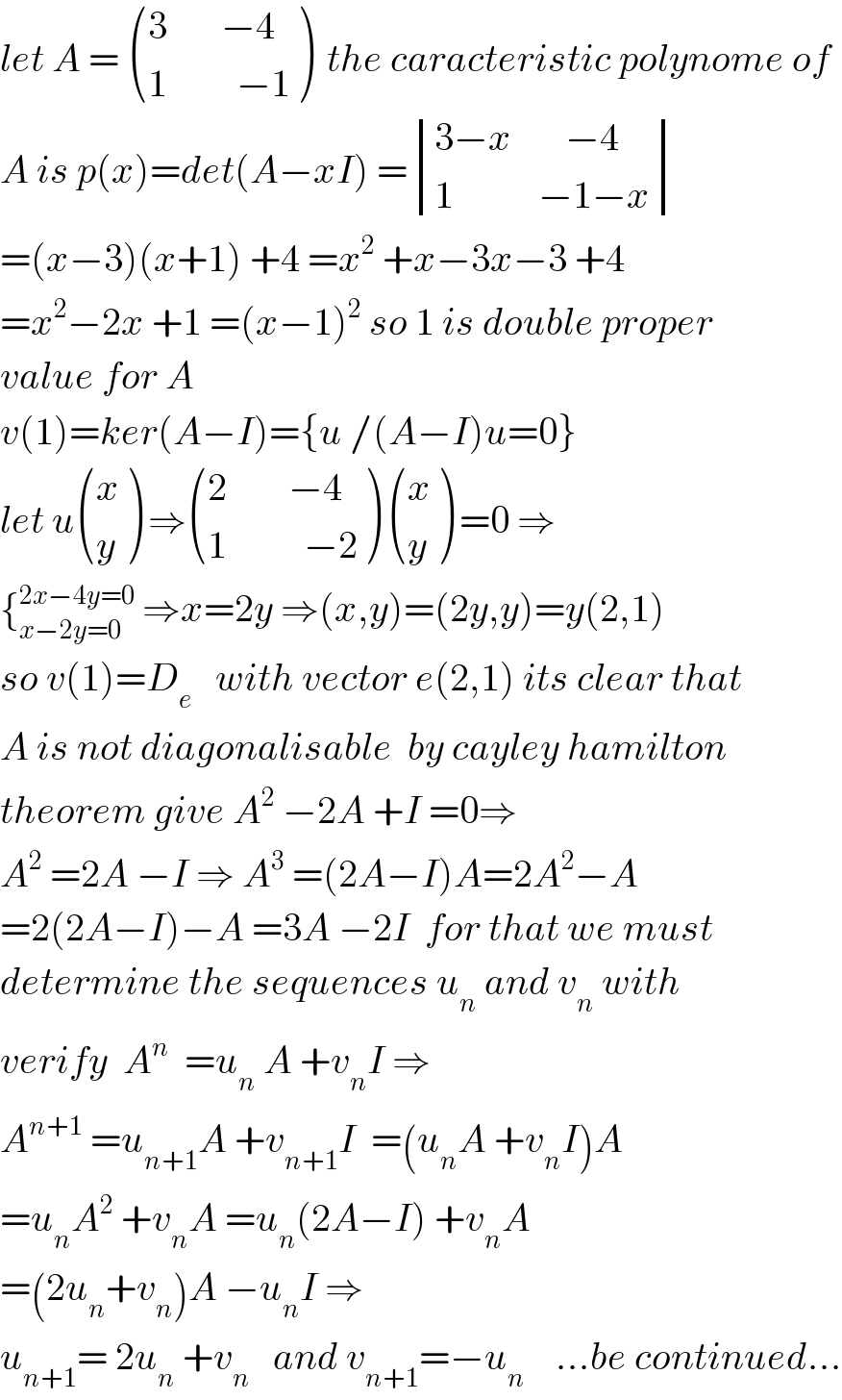
| ||
Question and Answers Forum | ||
Question Number 41141 by Kishan Daroga last updated on 02/Aug/18 | ||
![If X= [(3,(−4)),(1,(−1)) ], the value of X^n is](Q41141.png) | ||
Commented by math khazana by abdo last updated on 04/Aug/18 | ||
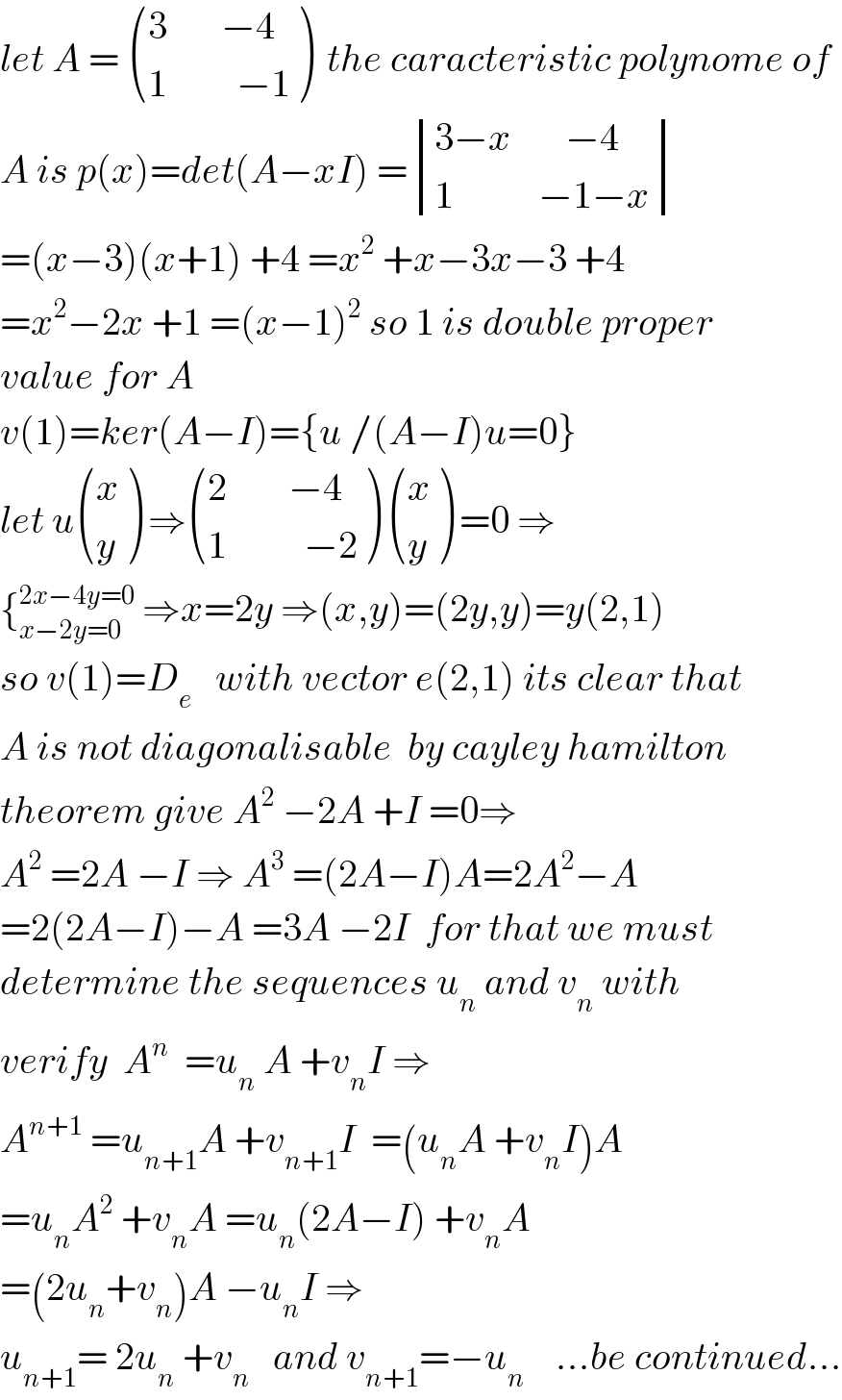 | ||