Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 4116 by Filup last updated on 29/Dec/15

For: f(x)=∣ax^n +b∣ when f(α) o f(β) is continuous, Does there exist a solution: S=∫_α ^( β) f(x)dx α<β

$$\mathrm{For}:\:{f}\left({x}\right)=\mid{ax}^{{n}} +{b}\mid \\ $$ $$\mathrm{when}\:{f}\left(\alpha\right)\:\mathrm{o}\:{f}\left(\beta\right)\:\mathrm{is}\:\mathrm{continuous}, \\ $$ $$\mathrm{Does}\:\mathrm{there}\:\mathrm{exist}\:\mathrm{a}\:\mathrm{solution}: \\ $$ $${S}=\int_{\alpha} ^{\:\beta} {f}\left({x}\right){dx} \\ $$ $$\alpha<\beta \\ $$

Commented byYozzii last updated on 29/Dec/15

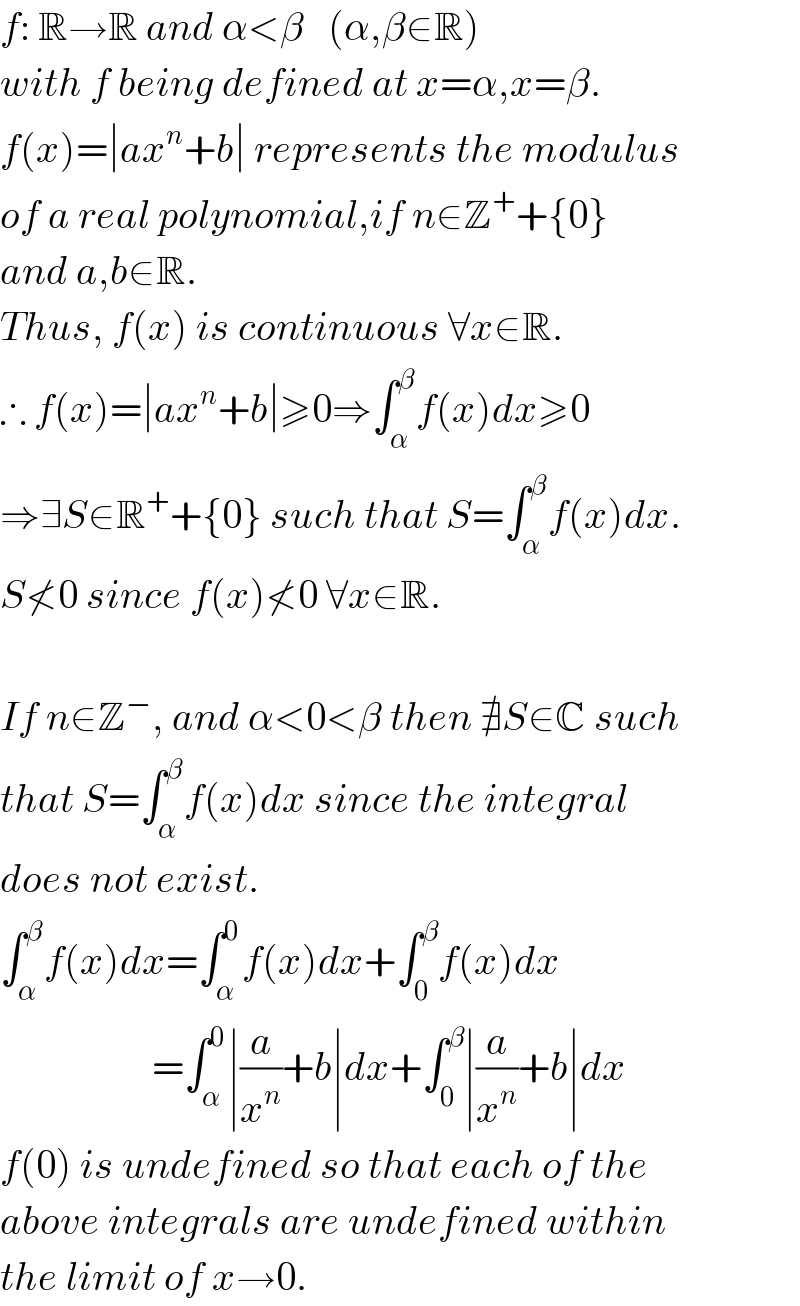
f: R→R and α<β (α,β∈R) with f being defined at x=α,x=β. f(x)=∣ax^n +b∣ represents the modulus of a real polynomial,if n∈Z^+ +{0} and a,b∈R. Thus, f(x) is continuous ∀x∈R. ∴ f(x)=∣ax^n +b∣≥0⇒∫_α ^β f(x)dx≥0 ⇒∃S∈R^+ +{0} such that S=∫_α ^β f(x)dx. S≮0 since f(x)≮0 ∀x∈R. If n∈Z^− , and α<0<β then ∄S∈C such that S=∫_α ^β f(x)dx since the integral does not exist. ∫_α ^β f(x)dx=∫_α ^0 f(x)dx+∫_0 ^β f(x)dx =∫_α ^0 ∣(a/x^n )+b∣dx+∫_0 ^β ∣(a/x^n )+b∣dx f(0) is undefined so that each of the above integrals are undefined within the limit of x→0.

$${f}:\:\mathbb{R}\rightarrow\mathbb{R}\:{and}\:\alpha<\beta\:\:\:\left(\alpha,\beta\in\mathbb{R}\right) \\ $$ $${with}\:{f}\:{being}\:{defined}\:{at}\:{x}=\alpha,{x}=\beta. \\ $$ $${f}\left({x}\right)=\mid{ax}^{{n}} +{b}\mid\:{represents}\:{the}\:{modulus} \\ $$ $${of}\:{a}\:{real}\:{polynomial},{if}\:{n}\in\mathbb{Z}^{+} +\left\{\mathrm{0}\right\} \\ $$ $${and}\:{a},{b}\in\mathbb{R}. \\ $$ $${Thus},\:{f}\left({x}\right)\:{is}\:{continuous}\:\forall{x}\in\mathbb{R}. \\ $$ $$\therefore\:{f}\left({x}\right)=\mid{ax}^{{n}} +{b}\mid\geqslant\mathrm{0}\Rightarrow\int_{\alpha} ^{\beta} {f}\left({x}\right){dx}\geqslant\mathrm{0} \\ $$ $$\Rightarrow\exists{S}\in\mathbb{R}^{+} +\left\{\mathrm{0}\right\}\:{such}\:{that}\:{S}=\int_{\alpha} ^{\beta} {f}\left({x}\right){dx}. \\ $$ $${S}\nless\mathrm{0}\:{since}\:{f}\left({x}\right)\nless\mathrm{0}\:\forall{x}\in\mathbb{R}. \\ $$ $$ \\ $$ $${If}\:{n}\in\mathbb{Z}^{−} ,\:{and}\:\alpha<\mathrm{0}<\beta\:{then}\:\nexists{S}\in\mathbb{C}\:{such} \\ $$ $${that}\:{S}=\int_{\alpha} ^{\beta} {f}\left({x}\right){dx}\:{since}\:{the}\:{integral} \\ $$ $${does}\:{not}\:{exist}.\: \\ $$ $$\int_{\alpha} ^{\beta} {f}\left({x}\right){dx}=\int_{\alpha} ^{\mathrm{0}} {f}\left({x}\right){dx}+\int_{\mathrm{0}} ^{\beta} {f}\left({x}\right){dx} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\int_{\alpha} ^{\mathrm{0}} \mid\frac{{a}}{{x}^{{n}} }+{b}\mid{dx}+\int_{\mathrm{0}} ^{\beta} \mid\frac{{a}}{{x}^{{n}} }+{b}\mid{dx} \\ $$ $${f}\left(\mathrm{0}\right)\:{is}\:{undefined}\:{so}\:{that}\:{each}\:{of}\:{the} \\ $$ $${above}\:{integrals}\:{are}\:{undefined}\:{within} \\ $$ $${the}\:{limit}\:{of}\:{x}\rightarrow\mathrm{0}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com