find the value of Σ_(n=2) ^∞ ((3n^2 +1)/((n^2 −1)^3 ))


Question and Answers Forum

All Questions Topic List
Relation and Functions Questions
Previous in All Question Next in All Question
Previous in Relation and Functions Next in Relation and Functions
Question Number 41236 by maxmathsup by imad last updated on 04/Aug/18

$f i n d t h e v a l u e o f \sum_{n = 2}^{\infty} \frac{3 n^{2} + 1}{{(n^{2} - 1)}^{3}}$
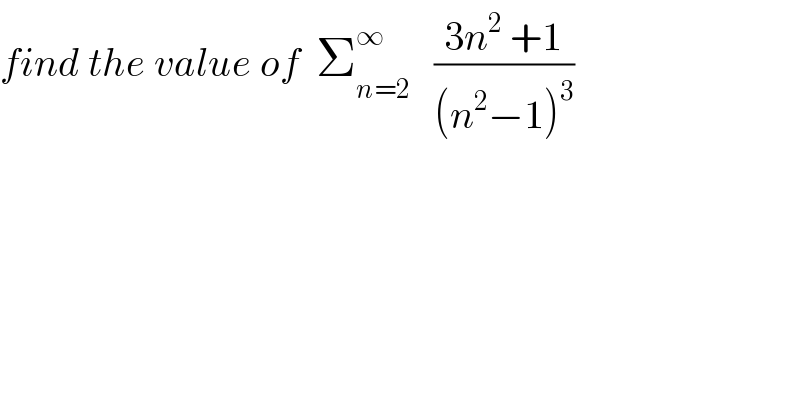
	Answered by tanmay.chaudhury50@gmail.com last updated on 04/Aug/18

	${(n + 1)}^{3} - {(n - 1)}^{3} = (n^{3} + 3 n^{2} + 3 n + 1) - (n^{3} - 3 n^{2} + 3 n - 1)$ $= 6^{} n^{2} + 2$ $\underset{n = 2}{\sum^{\infty}} \frac{1}{2} . \frac{{(n + 1)}^{3} - {(n - 1)}^{3}}{{(n + 1)}^{3} {(n - 1)}^{3}}$ $= \frac{1}{2} \underset{n = 2}{\sum^{\infty}} \frac{1}{{(n - 1)}^{3}} - \frac{1}{{(n + 1)}^{3}} = \frac{1}{2} \underset{2}{\sum^{\infty}} T_{n}$ $T_{n} = [\frac{1}{{(n - 1)}^{3}} - \frac{1}{{(n + 1)}^{3}}]$ $T_{2} = \frac{1}{1^{3}} - \frac{1}{3^{3}}$ $T_{3} = \frac{1}{2^{3}} - \frac{1}{4^{3}}$ $T_{4} = \frac{1}{3^{3}} - \frac{1}{5^{3}}$ $T_{5} = \frac{1}{4^{3}} - \frac{1}{6^{3}}$ $. . . .$ $. . . .$ $T_{n} = \frac{1}{{(n - 1)}^{3}} - \frac{1}{{(n + 1)}^{3}}$ $s = \frac{1}{1^{3}} + \frac{1}{2^{3}} - \frac{1}{{(n + 1)}^{3}}$ $\frac{1}{2} \underset{2}{\sum^{\infty}} T_{n} = \frac{1}{2} (1 + \frac{1}{8}) - \lim_{n \to \infty} \frac{1}{{(n + 1)}^{3}} = \frac{9}{16} - 0 = \frac{9}{16}$ $]$
	Commented by prof Abdo imad last updated on 04/Aug/18

	$y o u r a n s w e r i s c o r r e c t s i r T a n m a y t h a n k s$
	Commented by tanmay.chaudhury50@gmail.com last updated on 04/Aug/18

	$t h a n k y o u s i r . . .$
	Answered by prof Abdo imad last updated on 04/Aug/18
	$S =lim_(n→+∞) S_N with S_N =Σ_(n=2) ^N ((3n^(2 ) +1)/((n−1)^3 (n+1)^3 )) but we have (n+1)^3 −(n−1)^3 =2((n+1)^2 +(n+1)(n−1) +(n−1)^3 ) =2(n^2 +2n+1 +n^2 −1 +n^2 −2n+1) =2(3n^2 +1)⇒S_N =(1/2)Σ_(n=2) ^N (((n+1)^3 −(n−1)^3 )/((n−1)^3 (n+1)^3 )) =(1/2){Σ_(n=2) ^N (1/((n−1)^3 )) −Σ_(n=2) ^N (1/((n+1)^3 ))} but Σ_(n=2) ^N (1/((n−1)^3 )) =Σ_(n=1) ^(N−1) (1/n^3 ) =ξ_(N−1) (3) Σ_(n=2) ^N (1/((n+1)^3 )) =Σ_(n=3) ^(N+1) (1/n^3 ) =ξ_(N+1) (3)−1−(1/8) ⇒ S_N =(1/2){ ξ_(N−1) (3)−ξ_(N+1) (3) +(9/8)}but lim_(N→+∞) ξ_(N−1) (3)−ξ_(N+1) (3)=ξ(3)−ξ(3)=0⇒ lim_(N→+∞) S_N = (9/(16)) =S$
	$S = {l i m}_{n \to + \infty} S_{N} w i t h S_{N} = \sum_{n = 2}^{N} \frac{3 n^{2} + 1}{{(n - 1)}^{3} {(n + 1)}^{3}}$ $b u t w e h a v e {(n + 1)}^{3} - {(n - 1)}^{3}$ $= 2 ({(n + 1)}^{2} + (n + 1) (n - 1) + {(n - 1)}^{3})$ $= 2 (n^{2} + 2 n + 1 + n^{2} - 1 + n^{2} - 2 n + 1)$ $= 2 (3 n^{2} + 1) \Rightarrow S_{N} = \frac{1}{2} \sum_{n = 2}^{N} \frac{{(n + 1)}^{3} - {(n - 1)}^{3}}{{(n - 1)}^{3} {(n + 1)}^{3}}$ $= \frac{1}{2} {\sum_{n = 2}^{N} \frac{1}{{(n - 1)}^{3}} - \sum_{n = 2}^{N} \frac{1}{{(n + 1)}^{3}}} b u t$ $\sum_{n = 2}^{N} \frac{1}{{(n - 1)}^{3}} = \sum_{n = 1}^{N - 1} \frac{1}{n^{3}} = ξ_{N - 1} (3)$ $\sum_{n = 2}^{N} \frac{1}{{(n + 1)}^{3}} = \sum_{n = 3}^{N + 1} \frac{1}{n^{3}} = ξ_{N + 1} (3) - 1 - \frac{1}{8} \Rightarrow$ $S_{N} = \frac{1}{2} {ξ_{N - 1} (3) - ξ_{N + 1} (3) + \frac{9}{8}} b u t$ ${l i m}_{N \to + \infty} ξ_{N - 1} (3) - ξ_{N + 1} (3) = ξ (3) - ξ (3) = 0 \Rightarrow$ ${l i m}_{N \to + \infty} S_{N} = \frac{9}{16} = S$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum