
Question and Answers Forum
Question Number 41255 by ajfour last updated on 04/Aug/18
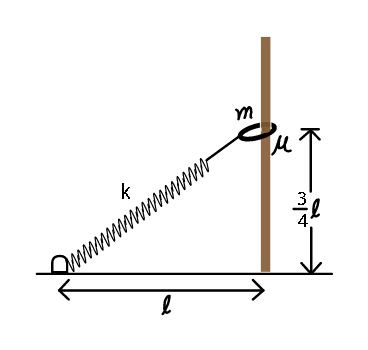
Commented by ajfour last updated on 04/Aug/18

Answered by ajfour last updated on 05/Aug/18
![At an intermediate position, let the angle of spring line with horizontal be θ. Normal reaction on ring N=kxcos θ x=l(sec θ−1) friction f = μkl(1−cos θ) height of ring is y=ltan θ dy = lsec^2 θdθ W_f =∫_α ^( 0) μkl^2 (1−cos θ)sec^2 θdθ where α = tan^(−1) ((3/4)) ⇒ W_f =−μkl^2 ∫_0 ^( α) (sec^2 θ−sec θ)dθ =−μkl^2 [tan α−ln (sec α+tan α)] =−μkl^2 [(3/4)−ln ((5/4)+(3/4))] =−μkl^2 ((3/4)−ln 2) (1/2)mv^2 = mg(((3l)/4))+(1/2)k[lsec α−l]^2 −μkl^2 ((3/4)−ln 2) v^2 = ((3gl)/2)+((kl^2 )/(16m))−((μkl^2 )/m)((3/2)−2ln 2) v =(√(((3gl)/2)+((kl^2 )/(16m))−((μkl^2 )/m)((3/2)−2ln 2))) .](Q41287.png)
Commented by MrW3 last updated on 05/Aug/18

Answered by tanmay.chaudhury50@gmail.com last updated on 05/Aug/18
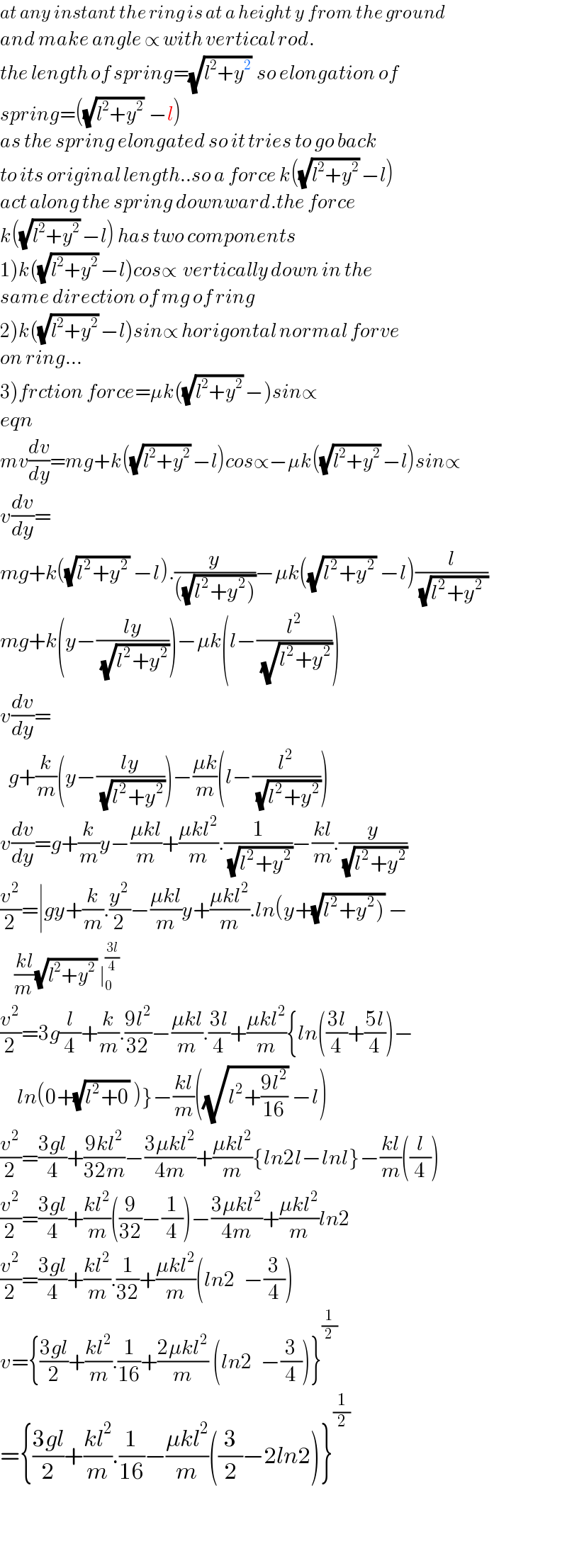
Commented by MrW3 last updated on 04/Aug/18

Commented by MrW3 last updated on 05/Aug/18
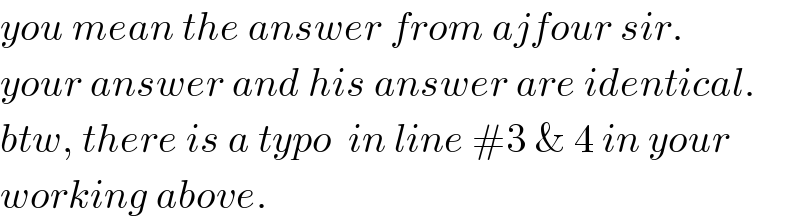
Commented by tanmay.chaudhury50@gmail.com last updated on 04/Aug/18

Commented by tanmay.chaudhury50@gmail.com last updated on 05/Aug/18

Commented by tanmay.chaudhury50@gmail.com last updated on 05/Aug/18

Commented by MrW3 last updated on 05/Aug/18

